今学期から物理と数学のスタディセンターでチューターをしています。 私は唯一の「純粋な」物理学チューターです – 残りのチューターは数学者やエンジニアで、数学を非常に快適に感じています（当然のことながら、彼らはすべて非常に素晴らしいです）。 しかし、彼らのほとんどは物理の問題を敬遠し、私や他の一握りのチューターに、この恐ろしい科目の処理を任せています。
一般に、物理には、問題を解き始める前に人を怖がらせるようなオーラがあるように思われます。 これは、非常に基本的な物理学から始まり、より高いレベルの教材でも続きます。
物理は、そしてほとんどの科学科目は、非常に複雑になる可能性があります。 私たちの世界を記述することは、必ずしも直感的ではなく、時には非常に高度な数学的、概念的理解を必要とします。 このことは、誰もが物理学のキャリアを目指すわけではないことを説明することができます。
基礎物理学、つまり高校や低レベルの大学の授業で扱われる内容では、方法論は単純です。 慌てる必要はないのです。
私は、低レベルの物理学クラスの家庭教師をした（あるいは受けた）経験から、問題を克服するのに役立ついくつかの基本的なルールを見つけ出しました。 これらは、問題が宿題であろうと試験であろうと役に立ちます。
Don’t Panic.
Sounds obvious, right? でも、案外難しいんです。 問題を見てみると、文章が威嚇するように迫ってきて、果てしなく混乱する。 基本的なコンセプトはわかっても、どこから手をつけていいのかわからない。 誰の車がどの方向に行くのか？ 糸を伝っていくのはどんな波なのか？ 助けてくれ、君は恐怖の中でそう思う。 助けて…！
今こそ深呼吸して目を閉じ、5つ数える時です。
下級物理では、ほとんどの問題は簡単な公式で解くことができます。 この公式さえ覚えていれば、答えまでの道のりはほとんど決まっています。 今後、あなたが集中しなければならないのは、恐ろしく混乱したテキストの塊を、あなたの公式に合わせて読みやすい断片に変換することだけです。
状況を理解する
この問題で何が起こっているのでしょうか。 これは、ある高さから自由落下するボールなのでしょうか。 ある距離のロイス・レインを救うために飛んでいるスーパーマンの速度でしょうか？ それとも、磁気の問題でしょうか？ 電気？
まず文脈を把握すること。 細かいことをすべて理解する必要はありませんが、一般的に何を扱っているのかがわかれば、どのように答えを作成し、どの方程式を使用すればよいかがわかります。 では、もう一度問題を読んで、実際に何を見つけることが要求されているのか、はっきりさせてください。 同じタイプの問題、例えばボールの跳ね返りの問題でも、初速、最大高さ、発射角度を求めることができます。 それぞれ、微妙に異なる戦略が必要になります。
この時点で覚えておくとよいもう一つのコツは、多くの物理学の問題には、非常に重要な情報が文言に含まれているということです。 例えば、車が静止状態から発進する場合、初速はゼロです。
問題を注意深く読むことです。 重要な情報を見逃さないようにしましょう。
情報の整理
言葉の問題は、その中の実際の変数を隠してしまうからこそ、混乱させるのです。 時には、本当に必要でない余分な情報が与えられることがあります。 また、問題の後半でその目的が明らかになる変数があることもあります。
例えば、車が静止状態から動き出し、時速20kmに達するまで5分かかるという問題なら、次のように基本変数を書きます：
これを問題から得た情報すべてで行う。 そうすることで、目の前の変数がはっきり見え、使うべき適切な式が見つかり、何が足りないのかがわかります。 また、元のわかりにくい文章が不要になります。
Sketch the Scene
物理学では、絵を描くことで物事を本当に簡単にすることができます。 例えば、参照枠や、上（プラス）と下（マイナス）の違いを視覚的に把握することが、正解と不正解の違いになります。
絵が上手でなくても構いません。 状況に応じて大まかな模式図を描いてください。 矢印は物理の問題の友です。物体がどの方向に動いているのか、あるいは物体にかかる力の和はどのようになるのかを示してくれます。 矢印は情報を整理してくれる。 9303>
いくつかの問題には、すでに図面が付属しています。 例えば力に関する問題は、模式図で解くのが一番です。スケッチしないと、すぐに見えない重要な情報を見逃してしまうことがあります。
さあ、ピカソ、全力を尽くして、次のステップに進みましょう。
単位の確認
時々、教授はあなたの単位変換スキルをテストすることがあります。 それは目的がないわけではありません。物理学（そして一般に科学）において、単位は非常に重要です。 物理学（そして科学全般）において、単位は非常に重要です。演習を通して単位が同じであることを確認しなければなりませんし、そうでなければ公式が成り立ちません。 速度に時間をかければ距離が求まりますが（加速度が一定と仮定）、車が時速10kmで5分間動いたとすると、10に5をかけても正しい答えにはなりません。 むしろ、時速キロメートルを分速キロメートルに変換するか、（おそらくもっと簡単な）5分を時間の単位に変換する必要があります。
これを行う最善の方法は分数ですが、この概念を説明する単位変換ガイドは十分に出回っています。
最後の部分から私たちの例を続ければ、t(final)を分から時間に変換する必要があります。 これはそれほど難しいことではありません。 * \frac{1 \text{ hour}}{60 \text{ minutes}} = \frac{1}{12}. \text{ hour})
(See how ‘minutes’ units are canceled with ‘minutes’ units in the denominator, leaving the ‘hour’ units with the final answer?分母の’分’の単位をキャンセルして、最終的に’時’の単位を残している。
これですべての変数が正しい単位になったので、問題を解き続けることができます。
公式を考える
これは物理問題のほとんどに言えることですが、低レベル物理では絶対に言えることでしょう。 基礎物理の学生として、あなたは車輪を再発明することを期待されていませんし、そもそも車輪がどのように発明されたかを理解することさえ期待されていません。
それらのツールの中で最も重要なのは公式です。
教授によっては、関連する公式の暗記を要求する人もいれば、「カンニングペーパー」をくれる人もいます。 いずれにせよ、あなたは必要なものを持っています。 暗記というと恐ろしいように聞こえるかもしれませんが、ほとんどの物理学の科目は、暗記すべき方程式がそれほど多くありません。 私は電磁気学の上級コースを受講していたのですが、そこで20種類ほどの数式を暗記しなければならなかったことを覚えています。 最初は大変そうで、間違って覚えてしまうこともありました。 しかし、公式を使えば使うほど、また、公式の意味や、気になるのであれば、公式がどこから来たのかを理解すればするほど、覚えるのが簡単になります。
公式を目の前で整理する。 チートシートがある場合は、変数の横に並べてください。 どのような式なら、変数の欠落を最小限に抑えて埋めることができるでしょうか。 どの式が問題を解くのに役立つか？
見る？ それを使ってください。
でも待って、どの公式を使えばいいの！
あなたは自分の公式シートを見て、問題の主題の下にマークされている3種類の公式があることを確認します。 どれを使えばいいのか、どうすればわかるのでしょうか？
物理式は、科学者が空から降ってきて、数学的な定式化できれいに包まれたわけではないのです。 物理的な性質から導き出されたものであり、それらはすべて相互に関連しているのです。 ほとんどの物理の問題では、解に到達する方法は1つではなく、2つ以上の方程式が成り立つことが多いのです。 実際、大半の問題では、どの方程式を使っても-それが主題に関連していて、適切な変数を入れると仮定すれば-解に到達します。
どの方程式を使うべきかを知る方法は、方程式で与えられた変数とあなたの経験という2つの主要問題に依存します。 問題を解けば解くほど、正しい式を選ぶための戦略に慣れてきます。 しかし、そうなるまでは、（変数のリストから）すでに知っている変数を持ち、それらを足りない1つの変数につなげる公式を探しましょう。 もし足りない変数が2つあれば、おそらく2つの式が必要になります。
ゆっくりと、変数リストを見て、正しいものを見つけてください。 これはパズルのようなもので、やればやるほどうまくなります。
Solve
変数があり、スケッチがあり、何が起こっているかわかっています。 目標を忘れないでください。 変数のリストに目をやり続けてください。 クエスチョンマークがついた変数がありますね。 それが、あなたが解かなければならない変数です。 集中するんだ ゴールを意識して
Now breathe.
Verify Your Results
このステップは多くの学生がスキップし、そして代償を払うことになるのです。 実際、私は高校の物理の期末試験で、その代償を払うことになりました。 結果を確認することは、方程式にざっと目を通し、得られた答えについて 15 秒考えるのと同じくらい簡単です。
その結果、100%と 70%、時にはそれ以上の差が生じることがあります。 まあ、車の速度で出た答えが光速以上だったら、間違ってる可能性が高いけど。 加速度の単位が適切な距離/時間^2の単位以外のものが出てきたなら、あなたは間違っている。 質問で分単位を求められ、答えが秒単位なら、手順を間違えたことになります。
説明書をよく読み、自分の方法を検証してください。 本当に大事なことです。
練習してください。 練習してください。 Practice.
でも、多くの生徒にはちゃんと伝わっていないようです。
30分かけて解いた問題の完璧な解き方を思いついたとき、家庭教師の生徒から驚いた顔をされることがあるんだ。 「私では思いつかなかった！」と、彼らは私の天才に畏敬の念を抱きます。 しかし、この褒め言葉は私のエゴですが、私は天才ではありません。 多くの問題を解いたので、どの方法が最も効果的であるか、すでに予想しているのです。 もちろん、そうではありません。 ある方法から始めて、それが間違った方法であったことに気づくこともあります。 しかし、そのような「誤り」は、異なる問題群にどのようにアプローチするかを教えてくれるにすぎません。
すべては経験なのです。 慌てず、あきらめず。 物理は思っているより（ほとんどの場合）難しくありません。
例題と解答
というわけで、一般物理問題の攻略法を構築してみた。 このオンラインドキュメントからピックアップしたサンプル問題を選んで、実際にどのように機能するかを見てみましょう。
問題
ある人が箱を40Nの力で床を斜めに引きずっています。 このとき、箱の質量は10kgである。 箱の加速度を3.5m/s^2とすると（摩擦は無視できる）、男は水平に対してどのような角度で引っ張るか。
戦略
- 慌てない
- 状況を把握する
この場合はかなり簡単です。 ある人が床の上の箱を引っ張っていますが、ただ斜めに引っ張っているだけです。 箱は前方に加速されます。前方の加速度についてしか説明されていないので、水平力（または水平投影）を考慮する必要があります – 垂直投影は今のところこの問題には関係ないようです。 それでも、箱に何らかの力がかかっていること、その力の角度を求めることが求められていることは認識できます。 - 情報を整理する
ここで、変数のリストを示します：- Force(man) = 40N
- m(box) = 10kg
- a(box) = 3.3.5 m/s^2
- SceneをSketchする
この場合、すでに元のドキュメントに図がありますが、わざと省いています。 自力でスケッチしてみてください。 箱があり、それを斜めに引っ張る力があります。 このように、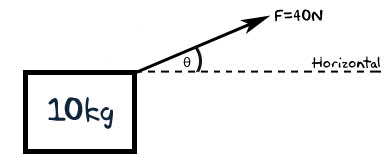
今、私たちは何を見つけることが期待され、何をすでに持っているかがわかります。 - 単位の確認
このケースでは、すべての単位が適合しています。 変換の必要はありません。 - 数式を考える
さて、基本的な力を扱う主な数式はこれです。- F=ma
- Cache(F_{Cachetext{x}}=F cos(\theta)\)
- Cache(F_{Cachetext{y}}=F sin(\theta)\)
式2、3は力のベクトルを分解したもの（意味が分からない人は、この式がおすすめ。 これらは、（分かっている）力と（求めたい）角度を結びつける式である。 そこで、加速度が水平にあるので、水平方向の力、またはその力の投影を考える必要があると述べました。 そして、F=maであることが分かっているので、加速度は力の直接の結果であることが分かります。 では、箱にかかる力は何でしょう？
{F_{text}}=m_{text}}a_{text}}=10}{kg}*3.5 m/s^2 = 35 \text{N}{}) {F_{text}{box}{a}}があります。 これは、加速度の原因となっている力です。このとき作用している力は、引っ張る人の力だけなので、その人の力の水平投影でなければなりません。投影のための三角形の公式を覚えていますか。 投影の三角形の公式を覚えていますか？水平成分を取って、今あるものを差し込んでみましょう。 - \(F_{CopyText{x}}=F cos(\theta)\)
- \(35=40 cos(\theta)\)
- \(\frac{7}{8}= cos(\theta)\)
- \(\theta=cos^{-1} (\frac{7}{8})\)
- \(\theta=28.XXX).96) これが答えだ。
- Verify Your Results
さて、ちょっと考えてみよう。 男はロープを斜めに引いている。 しかし、予想値（35N）は実際に使う力（40N）からそれほど離れていません。それなら、角度は比較的小さく、45度よりさらに小さくなるのは、非常に論理的です。
最後に…できましたね！
まとめ
取り組む前に、その話題にうんざりしないようにしてください。 物理は恐ろしく複雑に聞こえますが、その基本レベルの問題はほとんど似たようなものです。
つまり、要約すると、
- Don’t Panic.
- Try to understand the situation.（状況を理解すること。
- 質問を注意深く読む。
- 情報を整理する。
- 場面をスケッチする。
- 単位を確かめる。
- 計算式を考える。
- 解く。
- 結果を確かめる。
- 練習する。 練習する。 練習する.
そこで。 そんなに悪くなかったでしょ？
経験と自信と整理整頓です。 教材をよく勉強して、概念を理解し（たとえ数学が嫌いでも）、必要な方程式を理解する。 根気よく、整理して問題に取り組めば、突然物理が得意になるのがわかるはずです。 もしかしたら、とても優秀かもしれません。 9303>
物理の問題にアプローチする方法について、他に何かアドバイスはありますか？ ある種の問題で定期的に問題にぶつかることがありますか？
Credits
- UnintentonalChaos, for incredibly awesome editing help.
- Daniel Grrrrrrrrrrrrrreenberg, for his (as usual) keen eyes and good advice.
Daniel Grrrrrrrrrrrrrreenberg, for his (as usual) views.Don’t have an more advice with how to approach physics problems?
- Toby には、物理学があまり好きではないにもかかわらず、最終的な修正を指摘していただきました（完璧な人間などいません）。
- Picture credit: RLHyde from Flickr.