Dit semester ben ik begonnen met bijles geven in het natuurkunde en wiskunde studiecentrum. Ik ben de enige “pure” natuurkunde tutor – de rest van de tutoren zijn wiskundigen of ingenieurs die zich erg op hun gemak voelen met wiskunde (terecht, ze zijn allemaal behoorlijk geweldig). De meesten van hen schrikken echter terug voor natuurkundige problemen, en laten mij – en een handvol andere docenten – het gevreesde onderwerp behandelen.
In het algemeen lijkt natuurkunde een aura te hebben dat mensen afschrikt voordat ze zelfs maar beginnen met het oplossen van een probleem. Dit begint al bij de elementaire natuurkunde, maar gaat door bij het hogere niveau. Het verschil lijkt te zijn dat alleen degenen die van natuurkunde houden – en een goede manier vinden om ermee om te gaan – blijven hangen om zich met de hogere materie bezig te houden.
Fysica – en de meeste exacte vakken – kunnen erg ingewikkeld zijn. Het beschrijven van onze wereld is niet altijd intuïtief, en vereist soms een wiskundig en conceptueel begrip dat zeer geavanceerd is. Dat kan verklaren waarom niet iedereen voor een natuurkundige carrière kiest. Dat en, wel, het salaris.
In de basisfysica – materiaal dat op de middelbare school en in lage universitaire cursussen wordt behandeld – is de methodologie rechttoe rechtaan. Er is geen reden tot paniek. Heel vaak is het de paniek zelf die studenten ervan weerhoudt om zorgvuldig met het onderwerp om te gaan en het meeste uit die cursussen te halen.
In mijn ervaring met het geven van bijlessen voor (en het volgen van) natuurkundecursussen op laag niveau, heb ik een paar basisregels uitgewerkt die je kunnen helpen problemen te overwinnen. Deze zullen helpen of het probleem nu in een huiswerkopdracht of op een examen zit. We zullen ze nu doornemen.
Niet in paniek raken.
Klinkt voor de hand liggend, toch? En toch, het is moeilijker dan het klinkt. Je kijkt naar de vraag en de zinnen doemen dreigend op, verwarren je tot het einde. Je hebt geen idee waar je moet beginnen, ook al herken je de basisbegrippen. Wiens auto’s gaan in welke richting? Welk type golf beweegt op de snaar? Help me, denk je verschrikt. Help me…!
Dit is het moment om diep adem te halen, je ogen te sluiten, en tot vijf te tellen.
In de lagere natuurkunde kunnen de meeste vragen met eenvoudige formules worden opgelost. Zolang je deze formules onthoudt, ben je al een heel eind op weg naar een antwoord. Vanaf nu hoef je je alleen nog maar te concentreren op het omzetten van die afschuwelijke, verwarrende lap tekst in leesbare stukjes die in je formules passen. Dat kun je doen.
Probeer de situatie te begrijpen
Wat is er aan de hand in dit probleem? Is het een bal die van een hoogte in een vrije val valt? Is het de snelheid van Superman als hij Lois Lane op een bepaalde afstand komt redden? Of is het misschien een vraag over magnetisme? Elektriciteit?
Bedenk eerst de context. Je hoeft niet alle kleine details te begrijpen, maar als je eenmaal weet waar je in het algemeen mee te maken hebt, weet je hoe je je antwoord moet formuleren en welke vergelijkingen je moet gebruiken.
Lees de vraag aandachtig
Dus je begrijpt nu de fysische situatie, en je weet over welk onderwerp deze vraag gaat (of over meerdere onderwerpen). Lees de vraag nu nog eens, en zorg ervoor dat het je duidelijk is wat je eigenlijk moet vinden. Hetzelfde type probleem – bijvoorbeeld een stuiterende bal – kan je vragen om de beginsnelheid, de maximale hoogte of de lanceerhoek te vinden. Elk van deze zal een iets andere strategie vereisen. Zorg ervoor dat je weet wat je moet doen.
Een andere goede tip om ook op dit punt te onthouden, is dat veel natuurkundige problemen zeer cruciale informatie in de formulering hebben. Een auto die vanuit stilstand start, bijvoorbeeld, betekent dat je beginsnelheid nul is. Twee voorwerpen die uit een raam vallen, kunnen zich anders gedragen als ze aan elkaar vastzitten.
Lees de vraag aandachtig – dit is niet het moment om de vraag af te vinken. Zorg ervoor dat je geen cruciale informatie mist.
Organiseer de informatie
Woordproblemen zijn alleen verwarrend omdat ze de eigenlijke variabelen erin verbergen. Soms krijg je extra informatie die je niet echt nodig hebt. Andere keren, zullen er variabelen zijn waarvan het doel in een later deel van de vraag wordt onthuld.
Bij voorbeeld, als de vraag een auto betreft die vanuit stilstand begint te rijden en er 5 minuten over doet om een snelheid van 20 km/h te bereiken, dan moet u de basisvariabelen zo opschrijven:
- v(begin) = 0 km/h
- t(eind) = 5 minuten
- v(eind) = 20 km/h
- a = ?
Doe dit met alle informatie die je uit de vraag haalt. Dit zal je helpen om de variabelen duidelijk voor je te zien, de juiste vergelijking te vinden, en te zien wat je mist. Het zal ook de oorspronkelijke, verwarrende tekst onnodig maken. Als u uw informatie organiseert, zullen uw hersenen vrij zijn om zich bezig te houden met de werkelijke natuurkunde in plaats van met begrijpend lezen.
Sketch the Scene
In de natuurkunde kan het tekenen van een plaatje de dingen echt gemakkelijker maken. Bijvoorbeeld, het krijgen van een visueel idee van je referentiekader, of van het verschil tussen omhoog (positief) en omlaag (negatief), kan het verschil betekenen tussen een goed antwoord en een fout antwoord.
Je hoeft niet goed te zijn in tekenen. Teken een ruw schema op basis van de situatie. Pijlen zijn je vrienden bij natuurkundevragen – ze laten je zien in welke richting een voorwerp beweegt of wat de mogelijke som is van de krachten die erop worden uitgeoefend. Ze ordenen de informatie voor je. Gebruik ze.
Sommige vragen zijn al voorzien van een tekening – gebruik die! Vragen over krachten, bijvoorbeeld, zijn het best op te lossen door schematisch, en je kunt cruciale informatie missen die je niet meteen ziet als je het niet schetst.
Ga door, Picasso, geef het je beste schot, en ga door naar de volgende stap.
Verifieer Eenheden
Soms zal je professor je vaardigheden in het omrekenen van eenheden testen. Dat is niet zonder reden – in de natuurkunde (en de wetenschap in het algemeen), eenheden zijn van cruciaal belang. Je moet ervoor zorgen dat je eenheden gedurende de hele oefening hetzelfde zijn, anders werken formules niet. Als je de snelheid vermenigvuldigt met de tijd, krijg je de afstand (in de veronderstelling dat de versnelling constant is), maar als de auto gedurende 5 minuten 10 km per uur heeft gereden, krijg je het juiste antwoord niet als je 10 met 5 vermenigvuldigt. In plaats daarvan moet je ofwel de kilometers per uur omrekenen naar kilometers per minuut, of (en dat is waarschijnlijk gemakkelijker) 5 minuten omrekenen naar eenheden van uren.
De beste manier om dit te doen is door middel van breuken, maar er zijn genoeg omrekeningsgidsen voor eenheden die dit concept uitleggen. Denk eraan niet in paniek te raken, doe het voorzichtig en je zult je juiste waarden krijgen.
Als we ons voorbeeld van het laatste deel voortzetten, moeten we de t(final) omzetten van minuten naar uren. Dat is niet zo moeilijk:
(5 minuten} * \frac{1 \text{ uur}}{60 \text{ minuten}} = \frac{1}{12}
(Zie je hoe de ‘minuten’ eenheden worden geannuleerd met de ‘minuten’ eenheden in de noemer, waardoor de ‘uur’ eenheden overblijven met het uiteindelijke antwoord? Dat is een goede manier om te controleren of je omrekening klopt)
Nu al je variabelen in de juiste eenheden staan, kun je verder gaan met het oplossen van de vraag.
Bedenk je formules
Dit geldt voor de meeste natuurkundevragen, en absoluut voor de natuurkundevragen op een lager niveau. Als student basisnatuurkunde wordt niet van je verwacht dat je het wiel opnieuw uitvindt – of zelfs maar begrijpt hoe het wiel in de eerste plaats werd uitgevonden. Wat van je verwacht wordt, is dat je de concepten begrijpt en de hulpmiddelen gebruikt die je tot je beschikking hebt.
Het belangrijkste van die hulpmiddelen zijn de formules.
Sommige professoren zullen vereisen dat je relevante formules uit je hoofd leert, terwijl anderen je een “spiekbriefje” zullen geven. Hoe dan ook, je hebt wat je nodig hebt. Uit je hoofd leren klinkt misschien vreselijk, maar de meeste natuurkunde vakken hebben niet zo veel vergelijkingen om uit je hoofd te leren. Ik herinner me dat ik een cursus elektromagnetisme voor gevorderden volgde, waar ik zo’n 20 verschillende formules uit het hoofd moest leren. In het begin leek het verschrikkelijk, en ik bleef ze verkeerd onthouden. Maar hoe meer je de formules gebruikt, en hoe meer je begrijpt wat ze betekenen en – als je het wilt controleren – waar ze vandaan komen, hoe gemakkelijker je ze onthoudt.
Organiseer je formules voor je. Als je een spiekbriefje hebt, lijn het dan uit naast je variabelen. Welke formule kun je invullen, zodat er zo min mogelijk variabelen ontbreken? Welke formule kan je helpen de vraag op te lossen?
Zie je het? Gebruik hem.
Maar wacht, welke formule moet ik gebruiken?!
Je kijkt naar je formuleblad en je hebt drie verschillende die zijn aangegeven onder het onderwerp van het probleem. Hoe weet je welke je moet gebruiken? Natuurlijk begin je weer in paniek te raken.
Geen paniek.
Fysische vergelijkingen zijn niet zomaar uit de lucht komen vallen bij wetenschappers, allemaal mooi verpakt in wiskundige formules. Ze zijn afgeleid van fysische eigenschappen, en die zijn allemaal met elkaar verbonden. Bij de meeste natuurkundige problemen is er meer dan één manier om tot een oplossing te komen, wat vaak betekent dat meer dan één vergelijking kan werken. In feite, in de overgrote meerderheid van de vragen, maakt het niet uit welke vergelijking je gebruikt – ervan uitgaande dat het relevant is voor het onderwerp, en dat je de juiste variabelen invoegt – je zult tot een oplossing komen.
De manier om te weten welke vergelijking je moet gebruiken hangt af van twee belangrijke zaken: de variabelen die je in de vergelijking krijgt en je ervaring. Hoe meer problemen je oplost, hoe meer je vertrouwd raakt met strategieën om de juiste formule te kiezen. Maar tot het zover is, zoek de formule met de variabele die je al kent (uit je lijst van variabelen) en verbind die met de variabele die je nog mist. Als je twee ontbrekende variabelen hebt, heb je waarschijnlijk twee vergelijkingen nodig.
Doe rustig aan, kijk naar je variabelenlijst, en zoek de juiste. Het is als een puzzel, en hoe vaker je het doet, hoe beter je er in wordt.
Oplos
Je hebt je variabelen, je hebt je schets, je weet wat er aan de hand is – plug in, los op en krijg je antwoord.
Bedenk wel: je kunt eindigen met een relatief lange vergelijking om op te lossen, of soms twee (of meer). Vergeet je doel niet. Blijf kijken naar je lijst met variabelen. Zie je die kleine variabele gemarkeerd met een vraagteken, die je mist? Dat is de variabele die je moet oplossen. Concentreer je. Hou het doel voor ogen. Los de vergelijkingen op.
Nu ademhalen.
Verifieer je resultaten
Dit is een stap die veel studenten overslaan, en waar ze vervolgens voor boeten. Ik heb het me duur betaald bij mijn eindexamen natuurkunde op de middelbare school, en ik zal het nooit meer doen. Het verifiëren van de resultaten kan zo eenvoudig zijn als het doornemen van je vergelijkingen en 15 seconden nadenken over het antwoord dat je hebt gekregen.
Dat kan het verschil maken tussen 100% en 70%, en soms erger.
Wat bedoel ik met het verifiëren van het resultaat? Wel, als het antwoord dat je kreeg voor de snelheid van je auto meer is dan de lichtsnelheid, heb je het waarschijnlijk mis. Als de eenheden van versnelling iets anders blijken te zijn dan de juiste afstand/tijd^2 eenheden, heb je een fout gemaakt. Als je vraag om minuten vraagt en je antwoord is in seconden, heb je een stap gemist.
Lees de instructies zorgvuldig en controleer je methode. Het is echt belangrijk.
Oefenen. Practice. Oefenen.
Maar het lijkt voor veel studenten niet echt duidelijk te zijn.
Ik krijg soms verbaasde blikken van de studenten die ik bijles geef als ik de perfecte manier bedenk om een vraag op te lossen waar ze net een half uur mee bezig zijn geweest. “Daar zou ik nooit aan gedacht hebben!” roepen ze uit, vol ontzag voor mijn genialiteit. Nou, hoe graag mijn ego dit compliment ook zou aanvaarden, ik ben geen genie. De reden dat ik de oplossing snel zie, is meestal omdat ik ervaring heb – ik heb zoveel van deze vragen gedaan dat ik al weet welke methode waarschijnlijk het beste zou werken.
Heb ik het altijd bij het rechte eind? Natuurlijk niet. Soms begin ik met een methode en ontdek ik dat het de verkeerde manier was. Maar die “fouten” dienen alleen om je te leren hoe je verschillende vragen moet benaderen. Hoe vaker je ze doet, hoe minder tijd het je kost om de werkelijke effectieve manier om ze op te lossen te herkennen.
Het draait allemaal om ervaring. Raak niet in paniek en geef niet op. Natuurkunde is minder moeilijk dan je denkt (meestal).
Voorbeeldprobleem en oplossing
Dus we hebben geprobeerd een methode te construeren om algemene natuurkundige problemen aan te pakken. Laten we eens kijken hoe dit in de praktijk werkt door een voorbeeldvraag te kiezen die ik uit dit online document heb gehaald.
Het Probleem
Een man sleept een doos over de vloer met een kracht van 40N onder een hoek. De massa van de doos is 10kg. Als de versnelling van de doos 3,5 m/s^2 is (en wrijving kan worden verwaarloosd) onder welke hoek ten opzichte van de horizontaal trekt de man dan?
Strategie
- Niet in paniek raken.
- Probeer de situatie te begrijpen
In dit geval is het vrij eenvoudig. Een man trekt aan een doos op de grond, alleen trekt hij er schuin aan. De doos wordt voorwaarts versneld.Omdat ons alleen de voorwaartse versnelling wordt verteld, zullen we de horizontale krachten (of de horizontale projectie) moeten beschouwen – de verticale projectie lijkt vooralsnog niet relevant voor dit probleem. - Lees de vraag zorgvuldig
In dit geval is de vraag kort, en het is moeilijk om gegevens te missen. Toch weten we dat er een kracht op de doos staat, en dat van ons verwacht wordt dat we de hoek van die kracht vinden. Nu weten we wat we moeten doen, en kunnen we verder met de volgende stap. - De informatie ordenen
Hier is een lijst van onze variabelen:- Kracht(man) = 40N
- m(doos) = 10 kg
- a(doos) = 3.5 m/s^2
- Schets de scène
In dit geval staat er al een tekening in het originele document, maar die heb ik expres weggelaten. Probeer het zelf te schetsen. We hebben een doos, een kracht die er onder een hoek aan trekt. Zoals dit: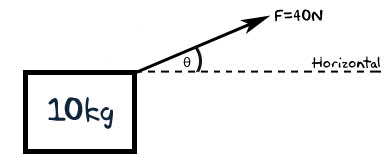
Nu kunnen we zien wat er van ons verwacht wordt, en wat we al hebben. - Eenheden verifiëren
Al onze eenheden passen in dit geval. Geen conversies nodig. - Overweeg uw formules
Wel, dit zijn de hoofdformules die over basiskrachten gaan:- F=ma
- (F_{text{x}}=F cos(\theta)\)
- (F_{text{y}}=F sin(\theta)\)
De formules #2 en #3 zijn de deconstructie van de krachtvector (als je niet weet wat dat betekent, moet je de stof nog eens doornemen) – dit zijn de formules die de kracht (die we kennen) koppelen aan de hoek (die we willen achterhalen)
- Oplossen
Herken je je nog ons “Begrijp het probleem”-gedeelte? We zeiden daar dat aangezien de versnelling horizontaal is, we de horizontale kracht of projectie van die kracht moeten beschouwen. En we weten dat F=ma, wat betekent dat de versnelling een direct gevolg is van de kracht. Wat is dan de kracht op de doos?
(F_{\box}}=m_{\box}}a_{\box}}=10 kg*3,5 m/s^2 = 35 \text{N}) Dit is de kracht die verantwoordelijk is voor de versnelling – en aangezien de enige kracht in het spel die van de trekkende man is, moet dit de horizontale projectie zijn van de kracht van die man. Herinner je je onze goniometrische formule voor de projectie? Laten we de horizontale component nemen, en inbrengen wat we hebben: - (F_text{x}}=F cos(\theta)\)
- (35=40 cos(\theta)\)
- (\frac{7}{8}= cos(\theta)\)
- (\theta=cos^{-1}(\frac{7}{8})\)
- (\theta=28.Dat is ons antwoord.
- Verifieer je resultaten
Wel, laten we hier eens even over nadenken. De man trekt onder een hoek aan het touw. Maar de projectie (35N) ligt niet ver af van de werkelijke kracht die hij gebruikt (40N) – het is dus heel logisch dat de hoek relatief klein zal zijn – zelfs kleiner dan 45 graden.
Psst… Het is je gelukt!
Samenvatting
Laat het onderwerp je niet in de steek voordat je er zelfs maar aan begonnen bent. Natuurkunde klinkt vreselijk ingewikkeld, maar de meeste basisvragen zijn vergelijkbaar – als je het concept eenmaal snapt, snap je de oplossing.
Dus, samengevat:
- Ga niet in paniek.
- Probeer de situatie te begrijpen.
- Lees de vraag aandachtig.
- Organiseer de informatie.
- Schets de scène.
- Verifieer de eenheden.
- Overweeg uw formules.
- Oplos.
- Verifieer uw resultaten.
- Oefenen. Practice. Oefenen.
Daar. Dat was niet zo slecht, toch?
Het gaat om ervaring, vertrouwen en organisatie. Bestudeer de stof goed, zodat je de concepten begrijpt (zelfs als je de wiskunde haat) en de vergelijkingen begrijpt die je moet gebruiken. Pak de problemen geduldig en met organisatie aan, en je zult zien hoe je ineens goed wordt in natuurkunde. Misschien zelfs heel goed. Misschien wordt het wel je hoofdvak op de universiteit!
Heb je nog meer advies over hoe je natuurkundevragen moet aanpakken? Loop je regelmatig tegen problemen aan met bepaalde soorten problemen? Voeg je input toe in de comments!
Credits
- UnintentonalChaos, voor ongelofelijk geweldige redactionele hulp.
- Daniel Grrrrrrrrrrrrrrreenberg, voor zijn (zoals gewoonlijk) scherpe blik en goede adviezen.
- Voor Toby, voor het aanwijzen van de laatste correcties, ook al vindt ze natuurkunde niet helemaal goed (niemand is perfect).
- Picture credit: RLHyde from Flickr.