Tänä lukuvuonna aloitin tuutoroinnin fysiikan ja matematiikan opintokeskuksessa. Olen ainoa ”puhdas” fysiikan tutor – muut tutorit ovat matemaatikkoja tai insinöörejä, jotka viihtyvät hyvin matematiikan parissa (syystäkin, he ovat kaikki aivan mahtavia). Useimmat heistä kuitenkin karttavat fysiikan ongelmia ja antavat minun – ja kourallisen muita tutoreita – hoitaa tämän pelätyn aiheen.
Yleisesti ottaen fysiikalla tuntuu olevan sellainen aura, joka pelottaa ihmisiä jo ennen kuin he edes alkavat ratkoa ongelmaa. Tämä alkaa hyvin perustason fysiikasta, mutta jatkuu korkeamman tason aineistossa. Ero näyttää olevan siinä, että vain ne, jotka pitävät fysiikasta – ja löytävät hyvän tavan käsitellä sitä – jäävät käsittelemään korkeamman tason aineita.
Fysiikka – ja useimmat luonnontieteelliset aineet – voivat olla hyvin monimutkaisia. Maailmamme kuvaaminen ei ole aina intuitiivista, ja joskus se vaatii matemaattista ja käsitteellistä ymmärrystä, joka on hyvin kehittynyttä. Se voi selittää, miksi kaikki eivät lähde fysiikan uralle. Se ja, no, palkka.
Fysiikan perusopinnoissa – lukion ja yliopistojen matalan tason kursseilla käsiteltävässä aineistossa – menetelmät ovat suoraviivaisia. Ei ole syytä paniikkiin. Aika usein juuri itse paniikki estää opiskelijoita käsittelemästä aihetta huolellisesti ja saamasta niistä kursseista kaiken mahdollisen irti.
Kokemukseni matalan tason fysiikan kurssien tukiopettajana (ja osallistujana) olen keksinyt muutamia perussääntöjä, jotka voivat auttaa sinua voittamaan ongelmat. Nämä auttavat riippumatta siitä, onko ongelma kotitehtävässä vai tentissä. Käymme ne nyt läpi.
Älkää hätääntykö.
Kuulostaa ilmeiseltä, eikö? Ja silti se on vaikeampaa kuin miltä se kuulostaa. Katsot kysymystä ja lauseet häämöttävät sinua uhkaavasti, hämmentäen sinua täysin. Sinulla ei ole aavistustakaan mistä aloittaa, vaikka tunnistaisitkin peruskäsitteet. Kenen autot kulkevat mihinkin suuntaan? Minkälainen aalto kulkee narussa? Auta minua, ajattelet kauhuissasi. Auttakaa minua…!
Tänään sinun on aika vetää syvään henkeä, sulkea silmäsi ja laskea viiteen.
Alemman tason fysiikassa useimmat kysymykset voidaan ratkaista yksinkertaisilla kaavoilla. Kunhan muistat nämä kaavat, olet suurimmaksi osaksi matkalla vastaukseen. Tästä eteenpäin ainoa asia, johon sinun tarvitsee keskittyä, on kauhean, sekavan tekstikappaleen muuntaminen luettaviksi paloiksi, jotka sopivat kaavoihisi. Voit tehdä sen.
Yritä ymmärtää tilanne
Mitä tässä ongelmassa tapahtuu? Onko kyseessä jostain korkeudesta vapaasti putoava pallo? Onko se Teräsmiehen nopeus, kun hän lentää pelastamaan Lois Lanen tietyn matkan päähän? Vai onko kyseessä kenties kysymys magnetismista? Sähköstä?
Selvitä ensin asiayhteys. Sinun ei tarvitse ymmärtää kaikkia pieniä yksityiskohtia, mutta kun tiedät, mistä yleisesti ottaen on kyse, osaat muotoilla vastauksesi ja mitä yhtälöitä käyttää.
Lue kysymys huolellisesti
Ymmärrät siis nyt fysikaalisen tilanteen ja tiedät, mitä aihetta tämä kysymys käsittelee (tai useampaa aihetta). Lue nyt kysymys uudelleen ja varmista, että olet selvillä siitä, mitä siinä oikeastaan vaaditaan löytämään. Samantyyppinen ongelma – vaikkapa pomppiva pallo – voi pyytää sinua löytämään alkunopeuden, maksimikorkeuden tai laukaisukulman. Kukin näistä edellyttää hieman erilaista strategiaa. Varmista, että tiedät, mitä sinun pitää tehdä.
Toinen hyvä vinkki muistettavaksi tässäkin vaiheessa on se, että monien fysiikan ongelmien sanamuodoissa on hyvin ratkaisevaa tietoa. Esimerkiksi levosta lähtevä auto tarkoittaa, että lähtönopeutesi on nolla. Kaksi ikkunasta putoavaa esinettä saattaa käyttäytyä eri tavalla, jos ne ovat molemmat kiinni toisissaan.
Lue kysymys huolellisesti – nyt ei ole aika sivuuttaa sitä. Varmista, ettet missaa ratkaisevaa tietoa.
Organisoi tietoa
Sanaongelmat ovat hämmentäviä vain siksi, että ne kätkevät sisäänsä varsinaiset muuttujat. Joskus sinulle annetaan lisätietoa, jota et oikeastaan tarvitse. Toisinaan taas on muuttujia, joiden tarkoitus paljastuu kysymyksen myöhemmässä osassa.
Jos kysymyksessä on esimerkiksi auto, joka lähtee liikkeelle levosta ja tarvitsee 5 minuuttia saavuttaakseen nopeuden 20 km/h, sinun pitäisi kirjoittaa perusmuuttujat ylös näin:
- v(alku) = 0 km/h
- t(loppu) = 5 minuuttia
- v(loppu) = 20 km/h
- a = ?
Tee tämä kaikilla tiedoilla, jotka saat kysymyksestä. Tämä auttaa sinua näkemään edessäsi olevat muuttujat selkeästi, löytämään oikean yhtälön, jota voit käyttää, ja näkemään, mitä sinulta puuttuu. Se tekee myös alkuperäisestä, sekavasta tekstistä tarpeetonta. Jos järjestät tietosi, aivosi ovat vapaat käsittelemään varsinaista fysiikkaa luetun ymmärtämisen sijaan.
Sketch the Scene
Fysiikassa kuvan piirtäminen voi todella helpottaa asioita. Esimerkiksi visuaalisen käsityksen saaminen viitekehyksestäsi tai ylös (positiivinen) ja alas (negatiivinen) välisestä erosta voi merkitä eroa oikean ja väärän vastauksen välillä.
Sinun ei tarvitse olla hyvä piirtämään. Piirrä karkea kaaviokuva tilanteen mukaan. Nuolet ovat ystäviäsi fysiikan kysymyksissä – ne osoittavat, mihin suuntaan kappale liikkuu tai mikä on siihen kohdistuvien voimien mahdollinen summa. Ne järjestävät tietoa puolestasi. Käytä niitä.
Joidenkin kysymysten mukana on jo piirros – käytä sitä! Esimerkiksi voimia koskevat kysymykset ratkaistaan parhaiten kaavamaisesti, ja voit jättää huomioimatta ratkaisevan tärkeää tietoa, jota et näe heti, jos et piirrä sitä.
Jatka, Picasso, anna kaikkesi ja siirry seuraavaan vaiheeseen.
Varmista yksiköt
Joskus professori testaa yksikkömuunnostaitojasi. Se ei ole tarkoituksetonta – fysiikassa (ja luonnontieteissä yleensä) yksiköt ovat ratkaisevan tärkeitä. Sinun on varmistettava, että yksikkösi ovat samat koko harjoituksen ajan, muuten kaavat eivät toimi. Jos kerrot nopeuden ajalla, saat etäisyyden (olettaen, että kiihtyvyys on vakio), mutta jos auto liikkui 10 km tunnissa 5 minuutin ajan, 10:n kertominen viidellä ei anna oikeaa vastausta. Pikemminkin sinun on joko muunnettava kilometrit tunnissa kilometreiksi minuutissa tai (mikä on luultavasti helpompaa) muunnettava 5 minuuttia tuntien yksiköiksi.
Paras tapa tehdä tämä on käyttää murtolukuja, mutta yksikkömuunnosoppaita, jotka selittävät tämän käsitteen, on tarpeeksi. Muista olla panikoimatta, tee se varovasti ja saat oikeat arvot.
Jatketaan esimerkkiä edellisestä osasta, meidän pitäisi muuntaa t(lopullinen) minuuteista tunneiksi. Tämä ei ole kovin vaikeaa:
\(5 \text{ minuuttia}) * \frac{1 \text{ tunti}}{60 \text{ minuuttia}} = \frac{1}{12}} \text{ tunti}\)
(Huomaatko, kuinka ’minuuttien’ yksiköt kumotaan nimittäjässä olevilla ’minuuttien’ yksiköillä, jolloin lopulliseksi vastaukseksi jää ’tunnin’ yksiköt? Se on hyvä tapa tarkistaa, että muunnoksesi on oikea)
Nyt kun kaikki muuttujasi ovat oikeissa yksiköissä, voit jatkaa kysymyksen ratkaisemista.
Harkitse kaavojasi
Tämä pätee suurimpaan osaan fysiikan kysymyksistä, ja täysin totta alemman tason fysiikassa. Perusfysiikan opiskelijana sinun ei odoteta keksivän pyörää uudelleen – tai edes ymmärtävän, miten pyörä ylipäätään keksittiin. Sinun odotetaan ymmärtävän käsitteet ja käyttävän käytettävissäsi olevia työkaluja.
Tärkeimmät näistä työkaluista ovat kaavat.
Jotkut professorit vaativat, että opettelet ulkoa asiaankuuluvat kaavat, kun taas toiset antavat sinulle ”huijauslomakkeen”. Oli miten oli, sinulla on se, mitä tarvitset. Muistaminen saattaa kuulostaa kauhealta, mutta useimmissa fysiikan oppiaineissa ei ole niin paljon yhtälöitä, jotka pitäisi muistaa ulkoa. Muistan käyneeni edistyneen sähkömagnetismin kurssin, jossa minun piti opetella ulkoa noin 20 erilaista kaavaa. Aluksi se tuntui kauhealta, ja muistin ne jatkuvasti väärin. Mitä enemmän kuitenkin käytät kaavoja ja mitä enemmän ymmärrät, mitä ne tarkoittavat ja – jos viitsit tarkistaa – mistä ne ovat peräisin, sitä helpommaksi niiden muistaminen käy.
Organisoi kaavat eteesi. Jos sinulla on huijauslappu, kohdista se muuttujien viereen. Minkä kaavan pystyt täyttämään niin, että siitä jää vähiten puuttuvia muuttujia? Minkä kaavan avulla voit ratkaista kysymyksen?
Näkyykö se? Käytä sitä.
Mutta odota, mitä kaavaa käytän?!
Katsot kaava-arkkiasi ja sinulla on kolme eri kaavaa, jotka on merkitty ongelman aiheen alle. Mistä tiedät, mitä niistä kannattaa käyttää?? Luonnollisesti alat taas panikoida.
Ei paniikkia.
Fyysiset yhtälöt eivät vain laskeutuneet tiedemiehille taivaalta, kaikki kauniisti käärittynä matemaattiseen muotoiluun. Ne on johdettu fysikaalisista ominaisuuksista, ja ne ovat kaikki yhteydessä toisiinsa. Useimmissa fysiikan ongelmissa on useampi kuin yksi tapa päästä ratkaisuun, mikä usein tarkoittaa, että useampi kuin yksi yhtälö voi toimia. Itse asiassa suurimmassa osassa kysymyksiä riippumatta siitä, mitä yhtälöä käytät – olettaen, että se on aiheen kannalta relevantti ja että asetat oikeat muuttujat – pääset ratkaisuun.
Tapa tietää, mitä yhtälöä kannattaa käyttää, riippuu kahdesta pääkysymyksestä: yhtälössä annetuista muuttujista ja kokemuksestasi. Mitä useampia ongelmia ratkaiset, sitä paremmin tunnet strategioita oikean kaavan valitsemiseksi. Siihen asti etsi kuitenkin kaavaa, jossa on jo tuntemasi muuttuja (muuttujien luettelosta) ja yhdistä ne siihen muuttujaan, joka puuttuu. Jos sinulla on kaksi puuttuvaa muuttujaa, tarvitset todennäköisesti kaksi yhtälöä.
Hiljaa, katso muuttujaluetteloasi ja etsi oikeat muuttujat. Se on kuin palapeli, ja mitä useammin teet sitä, sitä paremmaksi tulet siinä.
Ratkaise
Sinulla on muuttujasi, sinulla on luonnos, tiedät mitä on tekeillä – liitä, ratkaise ja saat vastauksesi.
Muista vain: saatat päätyä ratkaisemaan suhteellisen pitkän yhtälön tai joskus kaksi (tai enemmän). Älä unohda tavoitettasi. Vilkaise jatkuvasti muuttujien luetteloa. Näetkö tuon pienen kysymysmerkillä merkityn muuttujan, joka huomaa, että se puuttuu? Se on se, joka sinun on ratkaistava. Keskity. Pidä tavoite mielessäsi. Ratkaise yhtälöt.
Hengitä nyt.
Varmista tuloksesi
Tämä on vaihe, jonka monet opiskelijat jättävät väliin ja maksavat sitten siitä. Itse maksoin siitä kalliisti lukion fysiikan loppukokeessa, enkä tee sitä enää koskaan. Tulosten tarkistaminen voi olla yhtä helppoa kuin yhtälöiden läpikäyminen ja 15 sekunnin miettiminen saamasi vastauksen suhteen.
Se voi tehdä eron 100 %:n ja 70 %:n välillä, ja joskus huonomminkin.
Mitä tarkoitan tulosten tarkistamisella? No, jos saamasi vastaus autosi nopeudelle on suurempi kuin valonnopeus, olet todennäköisesti väärässä. Jos kiihtyvyyden yksiköiksi tulee jotain muuta kuin oikeat etäisyys/aika^2 -yksiköt, teit virheen. Jos kysymyksesi kysyy minuutteja ja vastauksesi on sekunneissa, unohdit askeleen.
Lue ohjeet huolellisesti ja tarkista menetelmäsi. Se on todella tärkeää.
Harjoittele. Harjoittele. Harjoittele.
Mutta se ei tunnu olevan kunnolla itsestään selvää monille opiskelijoille.
Minä saan joskus hämmästyneitä katseita opiskelijoilta, joita tutoroin, kun keksin täydellisen tavan ratkaista kysymys, jonka ratkaisemiseen he käyttivät juuri puoli tuntia. ”En olisi ikinä keksinyt sitä!” he huudahtavat ihaillen nerouttani. Niin paljon kuin egoni haluaisikin ottaa tämän kohteliaisuuden vastaan, en ole mikään nero. Syy siihen, että näen ratkaisun nopeasti, on yleensä se, että minulla on kokemusta – olen tehnyt niin monta tällaista kysymystä, että osaan jo ennakoida, mikä menetelmä todennäköisesti toimisi parhaiten.
Olenko aina oikeassa? En tietenkään ole. Joskus aloitan yhdellä menetelmällä ja huomaan, että se oli väärä tapa. Mutta nuo ”virheet” vain opettavat, miten lähestyä erilaisia kysymyssarjoja. Mitä useammin teet niitä, sitä vähemmän aikaa menee, ennen kuin tunnistat todellisen tehokkaan tavan ratkaista ne.
Kaikkea se on kokemuksesta kiinni. Älä panikoi äläkä luovuta. Fysiikka on vähemmän vaikeaa kuin luuletkaan (useimmiten).
Esimerkkiongelma ja ratkaisu
Olemme siis yrittäneet rakentaa menetelmän, jolla hyökkäämme yleisiin fysiikan ongelmiin. Katsotaanpa, miten tämä toimii käytännössä valitsemalla esimerkkikysymys, jonka poimin tästä verkkodokumentista.
Ongelma
Mies raahaa laatikkoa lattian poikki 40N:n voimalla vinosti. Laatikon massa on 10kg. Jos laatikon kiihtyvyys on 3,5 m/s^2 (ja kitka voidaan jättää huomiotta), missä kulmassa vaakatasoon nähden mies vetää?
Strategia
- Ei paniikkia.
- Yritä ymmärtää tilanne
Tässä tapauksessa tilanne on melko yksinkertainen. Mies vetää lattialla olevaa laatikkoa, mutta hän vetää sitä vinossa. Laatikko kiihtyy eteenpäin.Koska meille kerrotaan vain eteenpäin kiihtyvyydestä, meidän on otettava huomioon vaakasuuntaiset voimat (tai vaakaprojektio) – pystysuuntainen projektio ei näytä toistaiseksi olevan merkityksellinen tämän ongelman kannalta. - Lue kysymys huolellisesti
Tässä tapauksessa kysymys on lyhyt, ja on vaikea olla huomaamatta tietoja. Silti tunnistamme, että laatikkoon kohdistuu jokin voima ja että meidän odotetaan löytävän tuon voiman aiheuttaman kulman. Nyt tiedämme, mitä meidän pitää tehdä, ja voimme siirtyä seuraavaan vaiheeseen. - Järjestä tiedot
Tässä on luettelo muuttujistamme:- Force(man) = 40N
- m(box) = 10 kg
- a(box) = 3.5 m/s^2
- Sketch the Scene
Tässä tapauksessa alkuperäisessä dokumentissa on jo piirros, mutta jätin sen tarkoituksella pois. Yritä luonnostella se itse. Meillä on laatikko, jota voima vetää vinosti. Näin: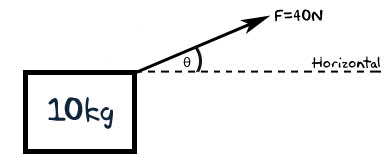
Nyt näemme, mitä meidän odotetaan löytävän ja mitä meillä jo on. - Tarkista yksiköt
Kaikki yksikkömme sopivat tähän tapaukseen. Mitään muunnoksia ei tarvita. - Tarkastele kaavojasi
Noh, nämä ovat tärkeimmät kaavat, jotka käsittelevät perusvoimia:- F=ma
- \(F_{\text{x}}=F cos(\theta)\)
- \(F_{\text{y}}=F sin(\theta)\)
Kaavat #2 ja #3 ovat voimavektorin dekonstruktiota (jos et tiedä mitä se tarkoittaa, sinun pitäisi käydä materiaali läpi) – nämä ovat kaavoja, jotka yhdistävät voiman (jonka tiedämme) kulmaan (jonka haluamme selvittää)
- Ratkaise
Muistatko ”Ymmärrä ongelma” -osamme? Sanoimme siinä, että koska kiihtyvyys on vaakatasossa, meidän on otettava huomioon vaakavoima tai sen projektio. Ja tiedämme, että F=ma, mikä tarkoittaa, että kiihtyvyys on suoraan seurausta voimasta. Mikä on siis laatikkoon kohdistuva voima?
\(F_{\text{box}}=m_{\text{box}}a_{\text{box}}=10\text{ kg}*3.5 m/s^2 = 35 \text{N}\) Tämä on kiihtyvyydestä vastaava voima – ja koska ainoa vaikuttava voima on vetävän miehen aiheuttama voima, tämän on oltava tämän miehen voiman vaakasuora projektio.Muistatko trigonometrisen kaavan projektiota varten? Otetaan vaakakomponentti ja liitetään siihen se, mitä meillä on: - \(F_{\text{x}}=F cos(\theta)\)
- \(35=40 cos(\theta)\)
- \(\frac{7}{8}= cos(\theta)\)
- \(\theta=cos^{-1}(\frak{7}{8})\)\)
- \(\theta=28.96\) Joka on vastauksemme.
- Tarkista tuloksesi
No, mietitäänpä tätä hetki. Mies vetää köyttä vinosti. Mutta projektio (35N) ei ole kovin kaukana hänen käyttämästään todellisesta voimasta (40N) – on siis aivan loogista, että kulma on suhteellisen pieni – jopa pienempi kuin 45 astetta.
Psst… Sait sen tehtyä!
Yhteenveto
Älkää antako aiheen lamaannuttaa itseänne, ennen kuin edes tartutte siihen. Fysiikka kuulostaa hirvittävän monimutkaiselta, mutta useimmat sen perustason kysymykset ovat samanlaisia – kun ymmärrät käsitteen, saat myös ratkaisun.
Yhteenvetona siis:
- Älä panikoi.
- Yritä ymmärtää tilanne.
- Lue kysymys huolellisesti.
- Organisoi tiedot.
- Piirrä kohtaus.
- Varmista yksiköt.
- Harkitse kaavojasi.
- Ratkaise.
- Varmista tuloksesi.
- Harjoittele. Harjoittele. Practice.
There. Eihän se ollutkaan niin paha?
Tässä on kyse kokemuksesta, itseluottamuksesta ja organisoinnista. Opiskele materiaali hyvin, jotta ymmärrät käsitteet (vaikka vihaat matematiikkaa) ja ymmärrät yhtälöt, joita sinun täytyy käyttää. Ratkaise ongelmat kärsivällisesti ja organisoidusti, niin huomaat kuinka sinusta tulee yhtäkkiä hyvä fysiikassa. Ehkä jopa erittäin hyväksi. Hitto, ehkä teet siitä yliopistosi pääaineen!
Onko sinulla muita neuvoja siitä, miten lähestyä fysiikan kysymyksiä? Törmäätkö säännöllisesti ongelmiin tietyntyyppisten ongelmien kanssa? Lisää panoksesi kommentteihin!
Credits
- UnintentonalChaos, uskomattoman mahtavasta muokkausavusta.
- Daniel Grrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrreenberg, hänen (kuten tavallista) tarkasta silmistään ja hyvistä neuvoistaan.
- Tobylle, lopullisten korjausten osoittamisesta, vaikka hän ei aivan pidä fysiikasta (kukaan ei ole täydellinen).
- Kuvan luotto: RLHyde Flickristä.
.