Det finns tre olika sorters vin.
wine.target_names
Vi skapar ett DataFrame som innehåller både funktioner och klasser.
df = X.join(pd.Series(y, name='class'))
Linjär diskriminantanalys kan delas upp i följande steg:
- Beräkna spridningsmatriserna inom klassen och mellan klasserna
- Beräkna egenvektorer och motsvarande egenvärden för spridningsmatriserna
- Sortera egenvärdena och välj de bästa k
- Skapa en ny matris som innehåller egenvektorer som mappar till de k egenvärdena
- Få fram de nya egenskaperna (i.LDA-komponenter) genom att ta punktprodukten av data och matrisen från steg 4
Spridningsmatris inom klassen
Vi beräknar spridningsmatrisen inom klassen med hjälp av följande formel.
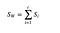
där c är det totala antalet distinkta klasser och
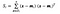

där x är ett stickprov (i.dvs. rad) och n är det totala antalet prov med en viss klass.
För varje klass skapar vi en vektor med medelvärdena för varje egenskap.

Därefter kopplar vi in medelvärdesvektorerna (mi) i ekvationen från tidigare för att erhålla spridningsmatrisen inom klassen.
Spridningsmatris mellan klasser
Nästan räknar vi ut spridningsmatrisen mellan klasser med följande formel.

där

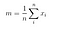
Därefter, löser vi det generaliserade egenvärdesproblemet för
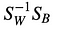
för att få fram de linjära diskriminanterna.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
De egenvektorer med de högsta egenvärdena bär på mest information om fördelningen av data. Därför sorterar vi egenvärdena från högst till lägst och väljer de första k egenvektorerna. För att säkerställa att egenvärdet mappar till samma egenvektor efter sorteringen placerar vi dem i en tillfällig array.

Om man bara tittar på värdena är det svårt att avgöra hur stor del av variansen som förklaras av varje komponent. Därför uttrycker vi det i procent.

Först skapar vi en matris W med de två första egenvektorerna.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Därefter sparar vi punktprodukten av X och W i en ny matris Y.
där X är en n×d-matris med n prover och d dimensioner, och Y är en n×k-matris med n prover och k ( k<n) dimensioner. Med andra ord består Y av LDA-komponenterna, eller sagt på ett annat sätt, det nya funktionsutrymmet.
X_lda = np.array(X.dot(w_matrix))
matplotlib kan inte hantera kategoriska variabler direkt. Därför kodar vi varje klass som ett nummer så att vi kan införliva klassbeteckningarna i vår plott.
le = LabelEncoder()y = le.fit_transform(df)
Därefter plottar vi data som en funktion av de två LDA-komponenterna och använder en annan färg för varje klass.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Istället för att implementera algoritmen för linjär diskriminantanalys från grunden varje gång kan vi använda den fördefinierade LinearDiscriminantAnalysis klass som gjorts tillgänglig för oss av scikit-learn-biblioteket.
Vi kan få tillgång till följande egenskap för att få fram den varians som förklaras av varje komponent.
lda.explained_variance_ratio_
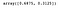
Samma som tidigare plottar vi de två LDA-komponenterna.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Nästan ska vi ta en titt på hur LDA kan jämföras med Principal Component Analysis eller PCA. Vi börjar med att skapa och anpassa en instans av klassen PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Vi kan komma åt egenskapen explained_variance_ratio_ för att se hur stor andel av variansen som förklaras av varje komponent.
pca.explained_variance_ratio_
Som vi kan se valde PCA de komponenter som skulle resultera i den största spridningen (behålla mest information) och inte nödvändigtvis de som maximerar separationen mellan klasserna.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Nästan ska vi se om vi kan skapa en modell för att klassificera med hjälp av LDA-komponenterna som funktioner. Först delar vi upp data i tränings- och testuppsättningar.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Därefter bygger vi upp och tränar ett beslutsträd. Efter att ha förutspått kategorin för varje prov i testuppsättningen skapar vi en förvirringsmatris för att utvärdera modellens prestanda.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
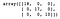
Som vi kan se klassificerar beslutsträdsklassificatorn korrekt allt i testuppsättningen.