Il y a 3 types de vin différents.
wine.target_names

Nous créons un DataFrame contenant à la fois les caractéristiques et les classes.
df = X.join(pd.Series(y, name='class'))
L’analyse discriminante linéaire peut être décomposée en plusieurs étapes :
- Calculer les matrices de diffusion à l’intérieur de la classe et entre les classes
- Calculer les vecteurs propres et les valeurs propres correspondantes pour les matrices de diffusion
- Trier les valeurs propres et sélectionner les k premières
- Créer une nouvelle matrice contenant les vecteurs propres qui correspondent aux k valeurs propres
- Obtenir les nouvelles caractéristiques (c’est-à-dire les composantes LDA) en prenant en compte les caractéristiques de la classe.c’est-à-dire les composantes LDA) en prenant le produit scalaire des données et de la matrice de l’étape 4
Matrice de dispersion intra-classe
Nous calculons la matrice de dispersion intra-classe en utilisant la formule suivante.
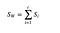
où c est le nombre total de classes distinctes et
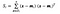

où x est un échantillon (c’est-à-dire une ligne) et n est le nombre de classes distinctes.c’est-à-dire une ligne) et n est le nombre total d’échantillons avec une classe donnée.
Pour chaque classe, nous créons un vecteur avec les moyennes de chaque caractéristique.

Puis, on branche les vecteurs moyens (mi) dans l’équation de tout à l’heure afin d’obtenir la matrice de diffusion intra-classe.
Matrice de diffusion inter-classe
Puis, on calcule la matrice de diffusion inter-classe en utilisant la formule suivante .

où

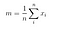
Alors, nous résolvons le problème des valeurs propres généralisées pour
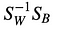
pour obtenir les discriminants linéaires.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Les vecteurs propres ayant les valeurs propres les plus élevées portent le plus d’informations sur la distribution des données. Ainsi, nous trions les valeurs propres du plus élevé au plus bas et nous sélectionnons les k premiers vecteurs propres. Afin de s’assurer que la valeur propre correspond au même vecteur propre après le tri, nous les plaçons dans un tableau temporaire.

En regardant simplement les valeurs, il est difficile de déterminer quelle part de la variance est expliquée par chaque composante. Ainsi, nous l’exprimons en pourcentage.

D’abord, nous créons une matrice W avec les deux premiers vecteurs propres.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Puis, nous enregistrons le produit scalaire de X et W dans une nouvelle matrice Y.
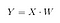
où X est une matrice n×d avec n échantillons et d dimensions, et Y est une matrice n×k avec n échantillons et k ( k<n) dimensions. En d’autres termes, Y est composé des composantes LDA, ou dit encore autrement, le nouvel espace de caractéristiques.
X_lda = np.array(X.dot(w_matrix))
matplotlib ne peut pas traiter directement les variables catégorielles. Ainsi, nous codons chaque classe comme un nombre afin que nous puissions incorporer les étiquettes de classe dans notre tracé.
le = LabelEncoder()y = le.fit_transform(df)
Puis, nous traçons les données en fonction des deux composantes LDA et utilisons une couleur différente pour chaque classe.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Plutôt que d’implémenter à chaque fois l’algorithme d’analyse discriminante linéaire à partir de zéro, nous pouvons utiliser la LinearDiscriminantAnalysis classe prédéfinie mise à notre disposition par la bibliothèque scikit-learn.
Nous pouvons accéder à la propriété suivante pour obtenir la variance expliquée par chaque composante.
lda.explained_variance_ratio_
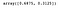
Comme précédemment, nous traçons les deux composantes LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Puis, regardons comment LDA se compare à l’analyse en composantes principales ou ACP. Nous commençons par créer et adapter une instance de la classe PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Nous pouvons accéder à la propriété explained_variance_ratio_ pour visualiser le pourcentage de la variance expliquée par chaque composante.
pca.explained_variance_ratio_
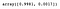
Comme nous pouvons le voir, l’ACP a sélectionné les composantes qui donneraient lieu à la plus grande dispersion (retenir le plus d’information) et pas nécessairement celles qui maximisent la séparation entre les classes.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Voyons ensuite si nous pouvons créer un modèle pour classer les en utilisant les composantes LDA comme caractéristiques. Tout d’abord, nous divisons les données en ensembles de formation et de test.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Puis, nous construisons et formons un arbre de décision. Après avoir prédit la catégorie de chaque échantillon dans l’ensemble de test, nous créons une matrice de confusion pour évaluer les performances du modèle.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
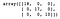
Comme nous pouvons le voir, le classificateur de l’arbre de décision a correctement classé tout ce qui se trouve dans l’ensemble de test.