Es gibt 3 verschiedene Arten von Wein.
wine.target_names

Wir erstellen einen DataFrame, der sowohl die Merkmale als auch die Klassen enthält.
df = X.join(pd.Series(y, name='class'))
Die lineare Diskriminanzanalyse lässt sich in die folgenden Schritte unterteilen:
- Berechnen Sie die Streumatrizen innerhalb der Klasse und zwischen den Klassen
- Berechnen Sie die Eigenvektoren und die entsprechenden Eigenwerte für die Streumatrizen
- Sortieren Sie die Eigenwerte und wählen Sie die obersten k
- Erstellen Sie eine neue Matrix, die Eigenvektoren enthält, die den k Eigenwerten entsprechen
- Erhalten Sie die neuen Merkmale (d. h.d. h. LDA-Komponenten), indem das Punktprodukt der Daten und der Matrix aus Schritt 4 gebildet wird
Streuungsmatrix innerhalb der Klasse
Wir berechnen die Streuungsmatrix innerhalb der Klasse anhand der folgenden Formel.
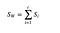
wobei c die Gesamtzahl der unterschiedlichen Klassen ist und
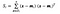

wobei x eine Stichprobe (d. h.d. h. Zeile) und n die Gesamtzahl der Stichproben mit einer bestimmten Klasse ist.
Für jede Klasse wird ein Vektor mit den Mittelwerten der einzelnen Merkmale erstellt.

Dann setzen wir die Mittelwertvektoren (mi) in die Gleichung von vorhin ein, um die Streumatrix innerhalb der Klasse zu erhalten.
Streumatrix zwischen den Klassen
Nächstens berechnen wir die Streumatrix zwischen den Klassen anhand der folgenden Formel.

wobei

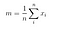
Dann, lösen wir das verallgemeinerte Eigenwertproblem für
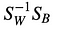
um die linearen Diskriminanten zu erhalten.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Die Eigenvektoren mit den höchsten Eigenwerten enthalten die meisten Informationen über die Verteilung der Daten. Wir sortieren also die Eigenwerte vom höchsten zum niedrigsten und wählen die ersten k Eigenvektoren aus. Um sicherzustellen, dass der Eigenwert nach der Sortierung auf denselben Eigenvektor abgebildet wird, legen wir sie in einem temporären Array ab.

Bei Betrachtung der Werte ist es schwierig zu bestimmen, wie viel der Varianz durch die einzelnen Komponenten erklärt wird. Daher drücken wir es als Prozentsatz aus.

Zuerst erstellen wir eine Matrix W mit den ersten beiden Eigenvektoren.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Dann speichern wir das Punktprodukt von X und W in einer neuen Matrix Y.
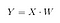
wobei X eine n×d-Matrix mit n Stichproben und d Dimensionen und Y eine n×k-Matrix mit n Stichproben und k ( k<n) Dimensionen ist. Mit anderen Worten, Y setzt sich aus den LDA-Komponenten zusammen, oder anders ausgedrückt, dem neuen Merkmalsraum.
X_lda = np.array(X.dot(w_matrix))
matplotlib kann kategoriale Variablen nicht direkt verarbeiten. Daher kodieren wir jede Klasse als Zahl, so dass wir die Klassenbezeichnungen in unsere Darstellung einbeziehen können.
le = LabelEncoder()y = le.fit_transform(df)
Dann stellen wir die Daten als Funktion der beiden LDA-Komponenten dar und verwenden für jede Klasse eine andere Farbe.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Anstatt den Algorithmus der linearen Diskriminanzanalyse jedes Mal von Grund auf neu zu implementieren, können wir die vordefinierten LinearDiscriminantAnalysis Klassen verwenden, die uns von der scikit-learnBibliothek zur Verfügung gestellt werden.
Wir können auf die folgende Eigenschaft zugreifen, um die durch jede Komponente erklärte Varianz zu erhalten.
lda.explained_variance_ratio_
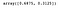
Wie zuvor stellen wir die beiden LDA-Komponenten dar.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Als Nächstes wollen wir uns ansehen, wie die LDA im Vergleich zur Hauptkomponentenanalyse oder PCA abschneidet. Wir beginnen mit der Erstellung und Anpassung einer Instanz der Klasse PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Wir können auf die Eigenschaft explained_variance_ratio_ zugreifen, um den prozentualen Anteil der Varianz zu sehen, der durch jede Komponente erklärt wird.
pca.explained_variance_ratio_
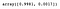
Wie wir sehen, hat die PCA die Komponenten ausgewählt, die die größte Streuung ergeben (die meisten Informationen enthalten) und nicht unbedingt die, die die Trennung zwischen den Klassen maximieren.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Als Nächstes wollen wir sehen, ob wir ein Modell erstellen können, das die LDA-Komponenten als Merkmale zur Klassifizierung verwendet. Zunächst werden die Daten in einen Trainings- und einen Testsatz aufgeteilt.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Dann wird ein Entscheidungsbaum erstellt und trainiert. Nach der Vorhersage der Kategorie jeder Probe im Testsatz erstellen wir eine Konfusionsmatrix, um die Leistung des Modells zu bewerten.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
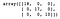
Wie wir sehen können, hat der Entscheidungsbaum-Klassifikator alles im Testsatz korrekt klassifiziert.