Er zijn 3 verschillende soorten wijn.
wine.target_names

We maken een DataFrame dat zowel de features als de klassen bevat.
df = X.join(pd.Series(y, name='class'))
Lineaire discriminantanalyse kan in de volgende stappen worden opgesplitst:
- Bereken de binnenklasse- en tussenklasse-verstrooiingsmatrices
- Bereken de eigenvectoren en overeenkomstige eigenwaarden voor de strooimatrices
- Sorteer de eigenwaarden en selecteer de top k
- Maak een nieuwe matrix met eigenvectoren die overeenkomen met de k eigenwaarden
- Bereken de nieuwe kenmerken (d. w. z.d. LDA-componenten) door het dot-product te nemen van de gegevens en de matrix uit stap 4
Spreidingsmatrix binnen klasse
We berekenen de spreidingsmatrix binnen klasse met behulp van de volgende formule.
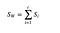
waar c het totale aantal verschillende klassen is en
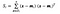

waar x een steekproef is (d.d.w.z. rij) is en n het totale aantal monsters met een bepaalde klasse.
Voor elke klasse creëren wij een vector met de gemiddelden van elk kenmerk.

Dan voegen we de gemiddelde vectoren (mi) in de vergelijking van hiervoor om de binnen klasse spreidingsmatrix te verkrijgen.
Tussen klasse spreidingsmatrix
Naar aanleiding hiervan berekenen we de tussen klasse spreidingsmatrix met behulp van de volgende formule.

waar

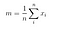
Dan, lossen we het veralgemeende eigenwaardeprobleem op voor
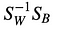
om de lineaire discriminanten te verkrijgen.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
De eigenvectoren met de hoogste eigenwaarden bevatten de meeste informatie over de verdeling van de gegevens. Daarom sorteren we de eigenwaarden van hoog naar laag en selecteren we de eerste k eigenvectoren. Om ervoor te zorgen dat de eigenwaarde na het sorteren aan dezelfde eigenvector wordt toegewezen, plaatsen we ze in een tijdelijke matrix.

Alleen door naar de waarden te kijken, is het moeilijk te bepalen hoeveel van de variantie door elke component wordt verklaard. Daarom drukken we het uit als percentage.

Eerst maken we een matrix W met de eerste twee eigenvectoren.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Daarna slaan we het scalair product van X en W op in een nieuwe matrix Y.
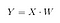
waar X een n×d matrix is met n steekproeven en d dimensies, en Y een n×k matrix is met n steekproeven en k ( k<n) dimensies. Met andere woorden, Y is samengesteld uit de LDA-componenten, of nog anders gezegd, de nieuwe feature space.
X_lda = np.array(X.dot(w_matrix))
matplotlib kan niet rechtstreeks omgaan met categorische variabelen. Daarom coderen we elke klasse als een getal, zodat we de klassenlabels in onze plot kunnen opnemen.
le = LabelEncoder()y = le.fit_transform(df)
Daarna zetten we de gegevens uit als functie van de twee LDA-componenten en gebruiken we voor elke klasse een andere kleur.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

In plaats van het Linear Discriminant Analysis algoritme iedere keer opnieuw te implementeren, kunnen we gebruik maken van de voorgedefinieerde LinearDiscriminantAnalysis klassen die ons door de scikit-learn bibliotheek ter beschikking worden gesteld.
We kunnen toegang krijgen tot de volgende eigenschap om de variantie te verkrijgen die door elke component wordt verklaard.
lda.explained_variance_ratio_
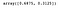
Net als voorheen zetten we de twee LDA-componenten uit.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Laten we nu eens kijken hoe LDA zich verhoudt tot Principal Component Analysis of PCA. We beginnen met het creëren en toepassen van een instantie van de klasse PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
We hebben toegang tot de eigenschap explained_variance_ratio_ om het percentage van de variantie te bekijken dat door elke component wordt verklaard.
pca.explained_variance_ratio_
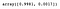
Zoals we kunnen zien, selecteerde PCA de componenten die in de hoogste spreiding zouden resulteren (de meeste informatie zouden vasthouden) en niet noodzakelijkerwijs die welke de scheiding tussen de klassen zouden maximaliseren.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Laten we nu eens kijken of we een model kunnen maken om de gegevens te classificeren met behulp van de LDA-componenten als kenmerken. Eerst splitsen we de gegevens op in training- en testsets.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Daarna bouwen en trainen we een beslisboom. Nadat we de categorie van elk monster in de testverzameling hebben voorspeld, maken we een verwarringsmatrix om de prestaties van het model te evalueren.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
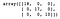
Zoals we kunnen zien, heeft de Decision Tree classificator alles in de testverzameling correct geclassificeerd.