Existují 3 různé druhy vína.
wine.target_names

Vytvoříme DataFrame obsahující rysy i třídy.
df = X.join(pd.Series(y, name='class'))
Lineární diskriminační analýzu lze rozdělit do následujících kroků:
- Vypočítejte matice rozptylu uvnitř třídy a mezi třídami
- Vypočítejte vlastní vektory a odpovídající vlastní hodnoty pro matice rozptylu
- Třiďte vlastní hodnoty a vyberte k nejlepších
- Vytvořte novou matici obsahující vlastní vektory, které mapují k vlastním hodnotám
- Získejte nové rysy (tj.tj. komponenty LDA) pomocí bodového součinu dat a matice z kroku 4
Matrice rozptylu uvnitř třídy
Matrici rozptylu uvnitř třídy vypočítáme podle následujícího vzorce.
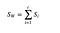
kde c je celkový počet různých tříd a
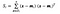

kde x je vzorek (tj.tj. řádek) a n je celkový počet vzorků s danou třídou.
Pro každou třídu vytvoříme vektor se střední hodnotou každého znaku.

Poté dosadíme vektory průměrů (mi) do rovnice z předchozího bodu, abychom získali matici rozptylu uvnitř třídy.
Matice rozptylu mezi třídami
Následujícím vzorcem vypočítáme matici rozptylu mezi třídami.

kde

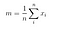
Pak, řešíme zobecněnou úlohu vlastních čísel pro
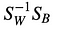
pro získání lineárních diskriminantů.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Vlastní vektory s nejvyššími vlastními hodnotami nesou nejvíce informací o rozdělení dat. Seřadíme tedy vlastní hodnoty od nejvyšší po nejnižší a vybereme prvních k vlastních vektorů. Abychom zajistili, že vlastní hodnota bude po setřídění mapována na stejný vlastní vektor, umístíme je do dočasného pole.

Při pouhém pohledu na hodnoty je obtížné určit, jak velkou část rozptylu vysvětlují jednotlivé komponenty. Vyjádříme to tedy v procentech.

Nejprve vytvoříme matici W s prvními dvěma vlastními vektory.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Poté uložíme tečkový součin X a W do nové matice Y. V případě, že se jedná o vlastní vektory, vytvoříme matici W s prvními dvěma vlastními vektory.
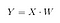
kde X je matice n×d s n vzorky a d rozměry a Y je matice n×k s n vzorky a k ( k<n) rozměry. Jinými slovy, Y se skládá z komponent LDA, nebo řečeno ještě jinak, z nového prostoru příznaků.
X_lda = np.array(X.dot(w_matrix))
matplotlib neumí přímo zpracovávat kategoriální proměnné. Proto každou třídu zakódujeme jako číslo, abychom mohli do našeho grafu začlenit značky tříd.
le = LabelEncoder()y = le.fit_transform(df)
Poté vykreslíme data jako funkci dvou komponent LDA a pro každou třídu použijeme jinou barvu.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Namísto toho, abychom pokaždé implementovali algoritmus lineární diskriminační analýzy od začátku, můžeme použít předdefinované LinearDiscriminantAnalysis třídy, které nám zpřístupňuje knihovna scikit-learn.
Můžeme přistupovat k následující vlastnosti, abychom získali rozptyl vysvětlený každou komponentou.
lda.explained_variance_ratio_
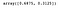
Stejně jako předtím vykreslíme obě komponenty LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Dále se podíváme na srovnání LDA s analýzou hlavních komponent neboli PCA. Začneme vytvořením a přizpůsobením instance třídy PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Můžeme přistupovat k vlastnosti explained_variance_ratio_ a zobrazit procento rozptylu vysvětlené každou komponentou.
pca.explained_variance_ratio_
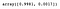
Jak vidíme, PCA vybrala komponenty, které by vedly k největšímu rozptylu (zachovaly nejvíce informací), a ne nutně ty, které maximalizují rozdělení mezi třídami.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Dále se podíváme, zda můžeme vytvořit model pro klasifikaci pomocí komponent LDA jako rysů. Nejprve rozdělíme data na trénovací a testovací množinu.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Poté sestavíme a natrénujeme rozhodovací strom. Po předpovědi kategorie každého vzorku v testovací množině vytvoříme matici záměny, abychom vyhodnotili výkonnost modelu.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
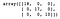
Jak vidíme, klasifikátor rozhodovacího stromu správně klasifikoval vše v testovací množině.
.