Linear Discriminant Analysis In Python

3種類のワインがあります。

wine.target_names

特徴とクラス両方を含むDataFrameを作成します。

df = X.join(pd.Series(y, name='class'))

線形判別分析は、以下のステップに分けることができる。

Within Class Scatter Matrix

クラス内散布行列を以下の式で計算する。

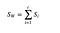
ここでcは異なるクラスの総数、

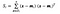
ここでxはサンプル（＝サンプル。行）、nは与えられたクラスを持つサンプルの総数です。

すべてのクラスについて、各特徴の平均を持つベクトルを作成します。

次に、クラス内散布行列を得るために平均ベクトル（mi）を先ほどの式に差し込む。

次に、以下の式でクラス間散布行列を計算する。

ここで

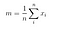
それでは。について一般化固有値問題を解き、

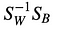
線形識別関数を得る。

eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))

最も高い固有値を持つ固有ベクトルはデータの分布に関する情報を最も多く持っています。従って、固有値を高いものから低いものへと並べ替え、最初のk個の固有ベクトルを選択する。ソート後の固有値が同じ固有ベクトルに対応するように、一時的な配列に入れます。

値だけを見ると、分散のどれくらいが各成分で説明されているか判断しにくいですね。そこで、パーセントで表します。

まず、最初の二つの固有ベクトルで行列Wを作ります。

w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real

そしてXとWのドットプロダクトで新しい行列Yに保存します。

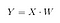
ここでXはnサンプル、d次元のn×d行列、Yはnサンプル、k（k＜6307＞n）次元のn×k行列である。言い換えれば、YはLDAの成分で構成され、別の言い方をすれば、新しい特徴空間である。

X_lda = np.array(X.dot(w_matrix))

matplotlibはカテゴリ変数を直接扱うことができない。

le = LabelEncoder()y = le.fit_transform(df)

次に、2つのLDA成分の関数としてデータをプロットし、各クラスに異なる色を使用します。

plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

毎回ゼロから線形判別アルゴリズムを実装するより、scikit-learnライブラリで利用できる定義済みLinearDiscriminantAnalysis クラスを使用することができるのです。

次のプロパティにアクセスして、各成分によって説明される分散を得ることができます。

lda.explained_variance_ratio_

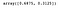
ちょうど前のように、2 つの LDA 成分をプロットします。

plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

次に、LDAと主成分分析（PCA）の比較を見ていきましょう。

from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)

explained_variance_ratio_ プロパティにアクセスして、各成分によって説明される分散の割合を見ることができます。

pca.explained_variance_ratio_

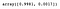
見てわかるように、PCAでは最も拡散する（最も情報を保つ）成分が選ばれ、必ずしもクラス間の分離を最大化する成分ではありません。

plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

次に、LDA成分を特徴として使って分類するモデルが作れるかどうか見てみましょう。まず、データをトレーニングセットとテストセットに分割します。

X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)

次に、決定木を構築してトレーニングします。テストセットの各サンプルのカテゴリを予測した後、モデルの性能を評価するために混同行列を作成する。

dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)

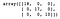
見てわかるように、決定木の分類器はテストセットのすべてを正しく分類している。