Ci sono 3 tipi diversi di vino.
wine.target_names

Creiamo un DataFrame contenente sia le caratteristiche che le classi.
df = X.join(pd.Series(y, name='class'))
L’analisi discriminante lineare può essere suddivisa nei seguenti passi:
- Computare le matrici di dispersione all’interno della classe e tra le classi
- Computare gli autovettori e gli autovalori corrispondenti per le matrici di dispersione
- Ordinare gli autovalori e selezionare i primi k
- Creare una nuova matrice contenente gli autovettori che mappano i k autovalori
- Ottenere le nuove caratteristiche (cioè le componenti di LDA) prendendo i componenti di LDA.e. componenti LDA) prendendo il prodotto di punti dei dati e la matrice dal passo 4
Matrice di dispersione interna alla classe
Calcoliamo la matrice di dispersione interna alla classe usando la seguente formula.
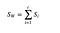
dove c è il numero totale di classi distinte e
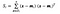

dove x è un campione (cioè.cioè la riga) e n è il numero totale di campioni con una data classe.
Per ogni classe, creiamo un vettore con le medie di ogni caratteristica.

Poi, inseriamo i vettori medi (mi) nell’equazione di prima per ottenere la matrice di dispersione all’interno della classe.
Matrice di dispersione tra classi
In seguito, calcoliamo la matrice di dispersione tra classi usando la seguente formula.

dove

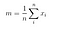
allora, risolviamo il problema degli autovalori generalizzati per
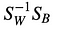
per ottenere i discriminanti lineari.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Gli autovettori con gli autovalori più alti portano più informazioni sulla distribuzione dei dati. Quindi, ordiniamo gli autovalori dal più alto al più basso e selezioniamo i primi k autovettori. Per assicurarci che l’autovalore corrisponda allo stesso autovettore dopo l’ordinamento, li mettiamo in un array temporaneo.

Solo guardando i valori, è difficile determinare quanta della varianza è spiegata da ogni componente. Così, la esprimiamo come percentuale.

Prima, creiamo una matrice W con i primi due autovettori.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Poi, salviamo il prodotto di punti di X e W in una nuova matrice Y.
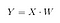
dove X è una matrice n×d con n campioni e d dimensioni, e Y è una matrice n×k con n campioni e k ( k<n) dimensioni. In altre parole, Y è composta dalle componenti di LDA, o detto ancora in un altro modo, il nuovo spazio delle caratteristiche.
X_lda = np.array(X.dot(w_matrix))
matplotlib non può gestire direttamente le variabili categoriali. Così, codifichiamo ogni classe come un numero in modo da poter incorporare le etichette di classe nel nostro grafico.
le = LabelEncoder()y = le.fit_transform(df)
Poi, tracciamo i dati in funzione delle due componenti LDA e usiamo un colore diverso per ogni classe.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Piuttosto che implementare l’algoritmo di Analisi Discriminante Lineare da zero ogni volta, possiamo usare le LinearDiscriminantAnalysis classi predefinite messe a nostra disposizione dalla libreria scikit-learn.
Possiamo accedere alla seguente proprietà per ottenere la varianza spiegata da ogni componente.
lda.explained_variance_ratio_
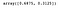
Come prima, tracciamo le due componenti LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

In seguito, diamo un’occhiata a come LDA si confronta con l’analisi delle componenti principali o PCA. Iniziamo creando e adattando un’istanza della classe PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Possiamo accedere alla proprietà explained_variance_ratio_ per visualizzare la percentuale della varianza spiegata da ogni componente.
pca.explained_variance_ratio_
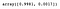
Come possiamo vedere, la PCA ha selezionato le componenti che avrebbero portato alla maggiore diffusione (trattenere più informazioni) e non necessariamente quelle che massimizzano la separazione tra le classi.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

In seguito, vediamo se possiamo creare un modello per classificare i usando le componenti LDA come caratteristiche. Per prima cosa, dividiamo i dati in insiemi di allenamento e di test.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Poi, costruiamo e addestriamo un albero di decisione. Dopo aver previsto la categoria di ogni campione nel set di test, creiamo una matrice di confusione per valutare le prestazioni del modello.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
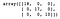
Come possiamo vedere, il classificatore Decision Tree ha classificato correttamente tutto nel set di test.