Háromféle bor van.
wine.target_names
Elkészítünk egy DataFrame-et, amely tartalmazza a jellemzőket és az osztályokat is.
df = X.join(pd.Series(y, name='class'))
A lineáris diszkriminanciaanalízis a következő lépésekre bontható:
- Kiszámítjuk az osztályon belüli és az osztályok közötti szórásmátrixokat
- Kiszámítjuk a szórásmátrixok sajátvektorait és a megfelelő sajátértékeket
- Válogatjuk a sajátértékeket és kiválasztjuk a legjobb k
- Készítünk egy új mátrixot, amely a k sajátértéknek megfelelő sajátvektorokat tartalmazza
- Megkapjuk az új jellemzőket (i.azaz LDA-komponensek) az adatok és a 4. lépésből származó mátrix pontszorzatával
Az osztályon belüli szórásmátrix
Az osztályon belüli szórásmátrixot a következő képlet segítségével számítjuk ki.
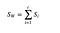
melyben c a különálló osztályok teljes száma és
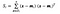

hol x egy minta (i.azaz sor) és n az adott osztályhoz tartozó minták teljes száma.
Minden osztályhoz létrehozunk egy vektort az egyes jellemzők átlagaival.

Ezután az átlagvektorokat (mi) beillesztjük az előző egyenletbe, hogy megkapjuk az osztályon belüli szórásmátrixot.
Közötti osztály szórásmátrix
A következő lépésben az osztályok közötti szórásmátrixot számítjuk ki a következő képlet segítségével.

hol

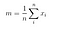
akkor, megoldjuk az
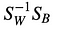
általánosított sajátérték-problémát, hogy megkapjuk a lineáris diszkriminánsokat.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
A legnagyobb sajátértékkel rendelkező sajátvektorok hordozzák a legtöbb információt az adatok eloszlásáról. Ezért a sajátértékeket a legnagyobbtól a legkisebbig sorba rendezzük, és kiválasztjuk az első k sajátvektort. Annak érdekében, hogy a rendezés után a sajátértékek ugyanahhoz a sajátvektorhoz kapcsolódjanak, egy ideiglenes tömbben helyezzük el őket.

Az értékeket csak megnézve nehéz meghatározni, hogy a variancia mekkora részét magyarázzák az egyes komponensek. Ezért ezt százalékban fejezzük ki.

Először létrehozunk egy W mátrixot az első két sajátvektorral.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Ezután az X és W pontproduktumát egy új Y mátrixba mentjük.
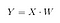
ahol X egy n×d mátrix n mintával és d dimenzióval, Y pedig egy n×k mátrix n mintával és k ( k<n) dimenzióval. Más szóval Y az LDA komponenseiből áll, vagy még másképp fogalmazva, az új jellemzőtér.
X_lda = np.array(X.dot(w_matrix))
matplotlib nem tud közvetlenül kategorikus változókat kezelni. Ezért minden osztályt számként kódolunk, hogy az osztálycímkéket beépíthessük a grafikonunkba.
le = LabelEncoder()y = le.fit_transform(df)
Ezután az adatokat a két LDA-komponens függvényében ábrázoljuk, és minden osztályhoz más színt használunk.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Ahelyett, hogy a lineáris diszkriminanciaanalízis algoritmust minden alkalommal a nulláról implementálnánk, használhatjuk a scikit-learnkönyvtár által rendelkezésünkre bocsátott előre meghatározott LinearDiscriminantAnalysis osztályokat.
Elérhetjük a következő tulajdonságot, hogy megkapjuk az egyes komponensek által magyarázott varianciát.
lda.explained_variance_ratio_
Az előzőekhez hasonlóan ábrázoljuk a két LDA-komponenst.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

A következőkben nézzük meg, hogyan viszonyul az LDA a főkomponens-elemzéshez vagy PCA-hoz. Kezdjük azzal, hogy létrehozzuk és illesztjük a PCA osztály egy példányát.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
A explained_variance_ratio_ tulajdonsághoz hozzáférhetünk, hogy megnézzük az egyes komponensek által magyarázott variancia százalékos arányát.
pca.explained_variance_ratio_
Amint láthatjuk, a PCA azokat a komponenseket választotta ki, amelyek a legnagyobb szórást eredményezik (a legtöbb információt tartják meg), és nem feltétlenül azokat, amelyek maximalizálják az osztályok közötti elkülönülést.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

A következőkben nézzük meg, hogy az LDA-komponensek mint jellemzők felhasználásával létrehozhatunk-e egy modellt az osztályozáshoz. Először is felosztjuk az adatokat gyakorló és tesztkészletekre.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Ezután létrehozunk és betanítunk egy döntési fát. Miután megjósoltuk az egyes minták kategóriáját a tesztkészletben, létrehozunk egy zavarmátrixot a modell teljesítményének értékeléséhez.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
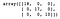
Amint látjuk, a döntési fa osztályozó helyesen osztályozott mindent a tesztkészletben.