Hay 3 tipos diferentes de vino.
wine.target_names

Creamos un DataFrame que contiene tanto las características como las clases.
df = X.join(pd.Series(y, name='class'))
El Análisis Discriminante Lineal puede dividirse en los siguientes pasos:
- Calcular las matrices de dispersión dentro de la clase y entre las clases
- Calcular los vectores propios y los correspondientes valores propios de las matrices de dispersión
- Ordenar los valores propios y seleccionar los k más importantes
- Crear una nueva matriz que contenga los vectores propios que se asignan a los k valores propios
- Obtener las nuevas características (es decir, los componentes del LDA) tomando como referencia los componentes del LDA.Es decir, componentes LDA) tomando el producto punto de los datos y la matriz del paso 4
Matriz de dispersión dentro de la clase
Calculamos la matriz de dispersión dentro de la clase utilizando la siguiente fórmula.
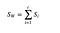
donde c es el número total de clases distintas y
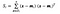

donde x es una muestra (i.es decir, fila) y n es el número total de muestras con una clase determinada.
Para cada clase, creamos un vector con las medias de cada característica.

A continuación, introducimos los vectores de medias (mi) en la ecuación anterior para obtener la matriz de dispersión dentro de la clase.
Matriz de dispersión entre clases
A continuación, calculamos la matriz de dispersión entre clases utilizando la siguiente fórmula.

donde

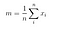
Entonces, resolvemos el problema de valores propios generalizado para
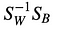
para obtener los discriminantes lineales.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Los vectores propios con los valores propios más altos llevan la mayor información sobre la distribución de los datos. Así, ordenamos los valores propios de mayor a menor y seleccionamos los primeros k vectores propios. Para garantizar que el valor propio se asigna al mismo vector propio después de la ordenación, los colocamos en una matriz temporal.

Sólo con mirar los valores, es difícil determinar qué parte de la varianza se explica por cada componente. Así, lo expresamos en forma de porcentaje.

Primero, creamos una matriz W con los dos primeros vectores propios.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
A continuación, guardamos el producto punto de X y W en una nueva matriz Y.
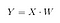
donde X es una matriz n×d con n muestras y d dimensiones, e Y es una matriz n×k con n muestras y k ( k<n) dimensiones. En otras palabras, Y se compone de los componentes de LDA, o dicho de otra manera, el nuevo espacio de características.
X_lda = np.array(X.dot(w_matrix))
matplotlib no puede manejar variables categóricas directamente. Por lo tanto, codificamos cada clase como un número para poder incorporar las etiquetas de clase en nuestro gráfico.
le = LabelEncoder()y = le.fit_transform(df)
Entonces, trazamos los datos como una función de los dos componentes LDA y utilizamos un color diferente para cada clase.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

En lugar de implementar el algoritmo de Análisis Lineal Discriminante desde cero cada vez, podemos utilizar la clase predefinida LinearDiscriminantAnalysis que pone a nuestra disposición la biblioteca scikit-learn.
Podemos acceder a la siguiente propiedad para obtener la varianza explicada por cada componente.
lda.explained_variance_ratio_
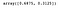
Al igual que antes, trazamos los dos componentes del LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

A continuación, vamos a ver cómo se compara el LDA con el Análisis de Componentes Principales o PCA. Comenzamos creando y ajustando una instancia de la clase PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Podemos acceder a la propiedad explained_variance_ratio_ para ver el porcentaje de la varianza explicada por cada componente.
pca.explained_variance_ratio_
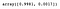
Como podemos ver, PCA seleccionó los componentes que darían lugar a la mayor dispersión (retener la mayor información) y no necesariamente los que maximizan la separación entre las clases.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

A continuación, vamos a ver si podemos crear un modelo para clasificar los utilizando los componentes del LDA como características. Primero, dividimos los datos en conjuntos de entrenamiento y de prueba.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Entonces, construimos y entrenamos un Árbol de Decisión. Después de predecir la categoría de cada muestra en el conjunto de prueba, creamos una matriz de confusión para evaluar el rendimiento del modelo.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
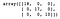
Como podemos ver, el clasificador del Árbol de Decisión clasificó correctamente todo en el conjunto de prueba.