Der er 3 forskellige slags vin.
wine.target_names
Vi opretter et DataFrame, der indeholder både features og klasser.
df = X.join(pd.Series(y, name='class'))
Linear Diskriminantanalyse kan opdeles i følgende trin:
- Beregne spredningsmatricerne inden for klassen og mellem klasserne
- Beregne egenvektorerne og de tilsvarende egenværdier for spredningsmatricerne
- Sortere egenværdierne og vælge de øverste k
- Opret en ny matrix, der indeholder egenvektorer, der kortlægger de k egenværdier
- Få de nye træk (i.dvs. LDA-komponenter) ved at tage prikproduktet af dataene og matricen fra trin 4
Indenfor-klasse-spredningsmatrix
Vi beregner indenfor-klasse-spredningsmatrixen ved hjælp af følgende formel.
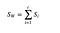
hvor c er det samlede antal forskellige klasser og
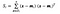

hvor x er en stikprøve (i.dvs. række) og n er det samlede antal prøver med en given klasse.
For hver klasse opretter vi en vektor med middelværdierne for hver egenskab.

Dernæst indsætter vi middelvektorerne (mi) i ligningen fra før for at opnå indenfor-klasse-spredningsmatrixen.
Mellem-klasse-spredningsmatrix
Næste gang beregner vi mellem-klasse-spredningsmatrixen ved hjælp af følgende formel.

hvor

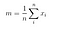
Derpå, løser vi det generaliserede egenværdiproblem for
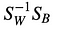
for at opnå de lineære diskriminanter.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Egenvektorerne med de højeste egenværdier indeholder mest information om fordelingen af dataene. Derfor sorterer vi egenværdierne fra højeste til laveste værdi og vælger de første k egenvektorer. For at sikre, at egenværdien kortlægger den samme egenvektor efter sorteringen, placerer vi dem i et midlertidigt array.

Kigger man blot på værdierne, er det svært at afgøre, hvor stor en del af variansen der forklares af hver komponent. Derfor udtrykker vi det som en procentdel.

Først opretter vi en matrix W med de to første egenvektorer.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Dernæst gemmer vi prikproduktet af X og W i en ny matrix Y.
hvor X er en n×d-matrix med n prøver og d dimensioner, og Y er en n×k-matrix med n prøver og k ( k<n) dimensioner. Med andre ord består Y af LDA-komponenterne, eller sagt på en anden måde, det nye feature space.
X_lda = np.array(X.dot(w_matrix))
matplotlib kan ikke håndtere kategoriske variabler direkte. Derfor koder vi hver klasse som et tal, så vi kan indarbejde klasselabels i vores plot.
le = LabelEncoder()y = le.fit_transform(df)
Dernæst plotter vi dataene som en funktion af de to LDA-komponenter og bruger en anden farve for hver klasse.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

I stedet for at implementere algoritmen Linear Discriminant Analysis fra bunden hver gang kan vi bruge den foruddefinerede LinearDiscriminantAnalysis klasse, der stilles til rådighed for os af scikit-learn-biblioteket.
Vi kan få adgang til følgende egenskab for at få den varians, der forklares af hver komponent.
lda.explained_variance_ratio_
Sådan som før plotter vi de to LDA-komponenter.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Næst skal vi se på, hvordan LDA kan sammenlignes med Principal Component Analysis eller PCA. Vi starter med at oprette og tilpasse en instans af PCA-klassen.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Vi kan få adgang til explained_variance_ratio_-egenskaben for at se den procentdel af variansen, der forklares af hver komponent.
pca.explained_variance_ratio_
Som vi kan se, valgte PCA de komponenter, som ville resultere i den største spredning (bevare mest information) og ikke nødvendigvis dem, som maksimerer adskillelsen mellem klasserne.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Næst skal vi se, om vi kan skabe en model til at klassificere den ved hjælp af LDA-komponenterne som features. Først opdeler vi dataene i et trænings- og et testsæt.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Dernæst opbygger og træner vi et beslutningstræ. Efter at vi har forudsagt kategorien for hver prøve i testsæt, opretter vi en forvirringsmatrix for at evaluere modellens ydeevne.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
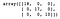
Som vi kan se, klassificerede beslutningstræklassificatoren alt i testsæt korrekt.