Există 3 tipuri diferite de vin.
wine.target_names

Creăm un DataFrame care conține atât caracteristicile cât și clasele.
df = X.join(pd.Series(y, name='class'))
Analiza discriminantă liniară poate fi împărțită în următoarele etape:
- Calculează matricile de dispersie în interiorul clasei și între clase
- Calculează vectorii proprii și valorile proprii corespunzătoare pentru matricile de dispersie
- Triază valorile proprii și selectează primele k
- Creează o nouă matrice care conține vectorii proprii care corespund celor k valori proprii
- Obține noile caracteristici (i.e. componentele LDA) prin realizarea produsului punctual al datelor și al matricei de la etapa 4
Matrice de dispersie în interiorul clasei
Calculăm matricea de dispersie în interiorul clasei folosind următoarea formulă.
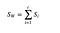
unde c este numărul total de clase distincte și
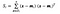

unde x este un eșantion (i.e. rând) și n este numărul total de eșantioane cu o anumită clasă.
Pentru fiecare clasă, creăm un vector cu mediile fiecărei caracteristici.

Apoi, introducem vectorii mediilor (mi) în ecuația de mai înainte pentru a obține matricea de dispersie în interiorul clasei.
Matrice de dispersie între clase
În continuare, calculăm matricea de dispersie între clase folosind următoarea formulă.

unde

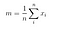
Atunci, rezolvăm problema valorilor proprii generalizate pentru
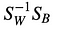
pentru a obține discriminanții liniari.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Vectori proprii cu cele mai mari valori proprii poartă cele mai multe informații despre distribuția datelor. Astfel, sortăm valorile proprii de la cea mai mare la cea mai mică și selectăm primii k vectori proprii. Pentru a ne asigura că valoarea proprie corespunde aceluiași vector propriu după sortare, le plasăm într-o matrice temporară.

Simplu uitându-ne la valori, este dificil să determinăm cât de mult din varianță este explicată de fiecare componentă. Astfel, o exprimăm în procente.

În primul rând, creăm o matrice W cu primii doi vectori proprii.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Apoi, salvăm produsul punctat al lui X și W într-o nouă matrice Y.
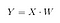
unde X este o matrice n×d cu n eșantioane și d dimensiuni, iar Y este o matrice n×k cu n eșantioane și k ( k<n) dimensiuni. Cu alte cuvinte, Y este compusă din componentele LDA sau, altfel spus, din noul spațiu al caracteristicilor.
X_lda = np.array(X.dot(w_matrix))
matplotlib nu poate gestiona direct variabilele categoriale. Astfel, codificăm fiecare clasă sub forma unui număr, astfel încât să putem încorpora etichetele de clasă în graficul nostru.
le = LabelEncoder()y = le.fit_transform(df)
Apoi, reprezentăm grafic datele ca o funcție a celor două componente LDA și folosim o culoare diferită pentru fiecare clasă.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

În loc să implementăm de fiecare dată de la zero algoritmul de analiză discriminantă liniară, putem folosi clasele predefinite LinearDiscriminantAnalysis puse la dispoziția noastră de biblioteca scikit-learn.
Potem accesa următoarea proprietate pentru a obține varianța explicată de fiecare componentă.
lda.explained_variance_ratio_
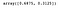
La fel ca înainte, reprezentăm grafic cele două componente LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

În continuare, să aruncăm o privire la modul în care LDA se compară cu Analiza Componentelor Principale sau PCA. Începem prin a crea și adapta o instanță a clasei PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Puteți accesa proprietatea explained_variance_ratio_ pentru a vizualiza procentul din varianța explicată de fiecare componentă.
pca.explained_variance_ratio_
După cum se poate observa, PCA a selectat componentele care să rezulte în cea mai mare răspândire (să rețină cele mai multe informații) și nu neapărat cele care maximizează separarea dintre clase.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

În continuare, să vedem dacă putem crea un model de clasificare a folosind componentele LDA ca caracteristici. În primul rând, împărțim datele în seturi de antrenament și de testare.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Apoi, construim și antrenăm un arbore de decizie. După ce am prezis categoria fiecărui eșantion din setul de testare, creăm o matrice de confuzie pentru a evalua performanța modelului.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
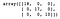
După cum putem vedea, clasificatorul Decision Tree a clasificat corect totul în setul de testare.