Existem 3 tipos diferentes de vinho.
wine.target_names
Criamos um DataFrame contendo tanto as características como as classes.
df = X.join(pd.Series(y, name='class'))
Análise Discriminatória Linear pode ser dividida nos seguintes passos:
- Calcular os valores próprios dentro da classe e entre matrizes de dispersão de classes
- Calcular os auto-vetores e os auto-valores correspondentes para as matrizes de dispersão
- Selecionar os auto-valores e selecionar o topo k
- Criar uma nova matriz contendo auto-vetores que mapeiam para os auto-valores k
- Manter as novas características (i.e. Componentes LDA) tomando o produto de pontos dos dados e a matriz do passo 4
Within Class Scatter Matrix
Calculamos a matriz de dispersão dentro da classe usando a seguinte fórmula.
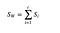
>
Em que c é o número total de classes distintas e
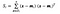
Onde x é uma amostra (i.e. linha) e n é o número total de amostras com uma determinada classe.
Para cada classe, nós criamos um vetor com as médias de cada característica.

Então, ligamos os vectores médios (mi) na equação de antes para obter a matriz de dispersão dentro da classe.
Matriz de dispersão entre classes
Próximo, calculamos a matriz de dispersão entre classes usando a seguinte fórmula.

where

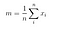
Então, resolvemos o problema do valor próprio generalizado para
para obter os discriminantes lineares.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Os auto-vectores com os valores mais elevados transportam a maior parte da informação sobre a distribuição dos dados. Assim, nós classificamos os autovalores do mais alto para o mais baixo e selecionamos os primeiros autovetores k. A fim de assegurar que os mapas de auto-valores para o mesmo auto-vetor após a ordenação, nós os colocamos em um array temporário.

Apenas olhando para os valores, é difícil determinar quanto da variância é explicada por cada componente. Assim, nós a expressamos como uma porcentagem.

Primeiro, nós criamos uma matriz W com os dois primeiros vetores próprios.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Então, nós salvamos o produto ponto de X e W em uma nova matriz Y.
onde X é uma matriz n×d com n amostras e d dimensões, e Y é uma matriz n×k com n amostras e k ( k<n) dimensões. Em outras palavras, Y é composto pelos componentes LDA, ou dito de outra forma, o novo espaço de características.
X_lda = np.array(X.dot(w_matrix))
matplotlib não pode lidar diretamente com variáveis categóricas. Assim, codificamos cada classe como um número para que possamos incorporar as etiquetas de classe em nosso gráfico.
le = LabelEncoder()y = le.fit_transform(df)
Então, plotamos os dados como uma função dos dois componentes LDA e usamos uma cor diferente para cada classe.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Reino do que implementar o algoritmo de Análise Discriminatória Linear a partir do zero, podemos usar a classe predefinida LinearDiscriminantAnalysis classe disponibilizada pela biblioteca scikit-learn.
Possibilidade de acessar a seguinte propriedade para obter a variância explicada por cada componente.
lda.explained_variance_ratio_
Apenas como antes, plotamos os dois componentes LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Próximo, vejamos como o LDA se compara à Análise de Componentes Principais ou PCA. Começamos criando e encaixando uma instância da classe PCA classe.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Podemos acessar a propriedade explained_variance_ratio_ para ver a porcentagem da variância explicada por cada componente.
pca.explained_variance_ratio_
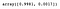
Como podemos ver, o PCA selecionou os componentes que resultariam na maior dispersão (retém a maior quantidade de informação) e não necessariamente os que maximizam a separação entre classes.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Próximo, vamos ver se podemos criar um modelo para classificar o uso dos componentes LDA como características. Primeiro, dividimos os dados em conjuntos de treinamento e testes.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Então, construímos e treinamos uma Árvore de Decisão. Após prever a categoria de cada amostra no conjunto de teste, criamos uma matriz de confusão para avaliar o desempenho do modelo.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
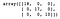
Como podemos ver, o classificador da Árvore de Decisão classificou corretamente tudo no conjunto de teste.