Istnieją 3 różne rodzaje win.
wine.target_names

Tworzymy DataFrame zawierającą zarówno cechy jak i klasy.
df = X.join(pd.Series(y, name='class'))
Liniowa Analiza Dyskryminacyjna może być podzielona na następujące kroki:
- Oblicz macierze rozproszenia wewnątrz klasy i między klasami
- Oblicz wektory własne i odpowiadające im wartości własne dla macierzy rozproszenia
- Sortuj wartości własne i wybierz k najlepszych
- Utwórz nową macierz zawierającą wektory własne, które odwzorowują k wartości własnych
- Uzyskaj nowe cechy (tj.tj. składowe LDA) przez wykonanie iloczynu punktowego danych i macierzy z kroku 4
Within Class Scatter Matrix
Obliczamy macierz rozproszenia wewnątrz klasy za pomocą następującego wzoru.
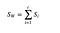
gdzie c jest całkowitą liczbą odrębnych klas i
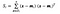

gdzie x jest próbką (tj.n jest całkowitą liczbą próbek z daną klasą.
Dla każdej klasy tworzymy wektor ze średnimi każdej cechy.

Następnie, wstawiamy wektory średnich (mi) do równania z wcześniej, aby otrzymać macierz rozrzutu wewnątrzklasowego.
Macierz rozrzutu międzyklasowego
Następnie, obliczamy macierz rozrzutu międzyklasowego używając następującego wzoru.

gdzie

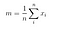
Wtedy, rozwiązujemy uogólniony problem wartości własnych dla
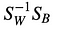
aby otrzymać wyróżniki liniowe.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Wektory własne o najwyższych wartościach własnych niosą najwięcej informacji o rozkładzie danych. Zatem sortujemy wartości własne od najwyższej do najniższej i wybieramy pierwsze k wektorów własnych. Aby zapewnić, że po posortowaniu wartość własna odpowiada temu samemu wektorowi własnemu, umieszczamy je w tablicy tymczasowej.

Patrząc tylko na wartości, trudno jest określić, jaka część wariancji jest wyjaśniona przez każdą składową. Wyrażamy ją więc w procentach.

Pierw tworzymy macierz W z dwoma pierwszymi wektorami własnymi.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Następnie zapisujemy iloczyn punktowy X i W do nowej macierzy Y.
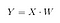
gdzie X jest macierzą n×d o n próbkach i d wymiarach, a Y jest macierzą n×k o n próbkach i k ( k<n) wymiarach. Innymi słowy, Y składa się z komponentów LDA, lub mówiąc inaczej, z nowej przestrzeni cech.
X_lda = np.array(X.dot(w_matrix))
matplotlib nie może bezpośrednio obsługiwać zmiennych kategorycznych. Dlatego kodujemy każdą klasę jako liczbę, abyśmy mogli włączyć etykiety klas do naszego wykresu.
le = LabelEncoder()y = le.fit_transform(df)
Następnie wykreślamy dane jako funkcję dwóch składowych LDA i używamy innego koloru dla każdej klasy.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Zamiast za każdym razem implementować algorytm liniowej analizy dyskryminacyjnej od zera, możemy skorzystać z predefiniowanych LinearDiscriminantAnalysis klas udostępnionych nam przez bibliotekę scikit-learn.
Możemy uzyskać dostęp do następującej właściwości, aby uzyskać wariancję wyjaśnioną przez każdą składową.
lda.explained_variance_ratio_
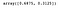
Tak jak poprzednio, wykreślamy dwie składowe LDA.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Następnie przyjrzyjmy się, jak LDA wypada w porównaniu z analizą składowych głównych, czyli PCA. Zaczniemy od utworzenia i dopasowania instancji klasy PCA.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Możemy uzyskać dostęp do właściwości explained_variance_ratio_, aby wyświetlić procent wariancji wyjaśnionej przez każdą składową.
pca.explained_variance_ratio_
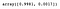
Jak widzimy, PCA wybrała te składowe, które spowodują największy rozrzut (zachowają najwięcej informacji), a niekoniecznie te, które maksymalizują separację między klasami.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Następnie sprawdźmy, czy możemy stworzyć model klasyfikujący przy użyciu składowych LDA jako cech. Najpierw dzielimy dane na zbiór treningowy i testowy.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Potem budujemy i trenujemy drzewo decyzyjne. Po przewidzeniu kategorii każdej próbki w zbiorze testowym tworzymy macierz konfuzji, aby ocenić wydajność modelu.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
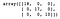
Jak widać, klasyfikator drzewa decyzyjnego poprawnie sklasyfikował wszystko w zbiorze testowym.
.