Viinoja on 3 erilaista.
wine.target_names
Luomme DataFrame-tietoruudun (DataFrame), joka sisältää sekä piirteet että luokat.
df = X.join(pd.Series(y, name='class'))
Lineaarinen diskriminaatioanalyysi voidaan jakaa seuraaviin vaiheisiin:
- Lasketaan luokan sisäiset ja luokkien väliset hajontamatriisit
- Lasketaan hajontamatriisien omavektorit ja vastaavat ominaissuureet
- Lajitellaan ominaissuureet ja valitaan k parasta
- Luotaan uusi matriisi, joka sisältää omavektorit, jotka vastaavat k:tta ominaissuureita
- Hankitaan uudet piirteet (esim.eli LDA-komponentit) ottamalla datan ja vaiheen 4 matriisin pistepotentiaali
Luokan sisäinen hajontamatriisi
Laskemme luokan sisäisen hajontamatriisin seuraavan kaavan avulla.
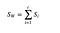
jossa c on erillisten luokkien kokonaismäärä ja
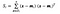

jossa x on näyte (i.eli rivi) ja n on tietyn luokan näytteiden kokonaismäärä.
Kullekin luokalle luodaan vektori, jossa on kunkin ominaisuuden keskiarvot.

Silloitamme sitten keskiarvovektorit (mi) edelliseen yhtälöön saadaksemme luokkien sisäisen hajontamatriisin.
Luokkien välisen hajontamatriisin
Seuraavaksi laskemme luokkien välisen hajontamatriisin seuraavan kaavan avulla.

jossa

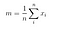
Tällöin, ratkaisemme yleistetyn ominaisarvo-ongelman
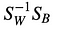
saadaksemme lineaariset diskriminanttitiedot.
eigen_values, eigen_vectors = np.linalg.eig(np.linalg.inv(within_class_scatter_matrix).dot(between_class_scatter_matrix))
Ominaisvektorit, joilla on suurimmat ominaisarvot, kantavat eniten tietoa aineiston jakaumasta. Näin ollen lajittelemme ominaisarvot suurimmasta pienimpään ja valitsemme ensimmäiset k ominaisvektoria. Varmistaaksemme, että lajittelun jälkeen ominaistietoarvot vastaavat samaa ominaistietovektoria, sijoitamme ne väliaikaiseen matriisiin.

Vain arvoja tarkastelemalla on vaikea päätellä, kuinka suuren osan varianssista kukin komponentti selittää. Niinpä ilmaisemme sen prosentteina.

Luotaan ensin matriisi W, jossa on kaksi ensimmäistä ominaisvektoria.
w_matrix = np.hstack((pairs.reshape(13,1), pairs.reshape(13,1))).real
Tallennetaan sitten X:n ja W:n pistepotentiaali uudeksi matriisiksi Y.
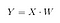
jossa X on n×d-matriisi, jossa on n näytettä ja d ulottuvuutta, ja Y on n×k-matriisi, jossa on n näytettä ja k ( k<n) ulottuvuutta. Toisin sanoen Y muodostuu LDA:n komponenteista tai toisin sanottuna uudesta piirreavaruudesta.
X_lda = np.array(X.dot(w_matrix))
matplotlib ei pysty käsittelemään suoraan kategorisia muuttujia. Niinpä koodaamme jokaisen luokan numeroksi, jotta voimme sisällyttää luokkamerkinnät kuvaajaamme.
le = LabelEncoder()y = le.fit_transform(df)
Sitten kuvaamme datan kahden LDA-komponentin funktiona ja käytämme eri väriä jokaiselle luokalle.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Sen sijaan, että toteuttaisimme lineaarisen diskriminanttianalyysin algoritmin joka kerta tyhjästä, voimme käyttää valmiita LinearDiscriminantAnalysis luokkia, jotka scikit-learn-kirjasto on asettanut käyttöömme.
Voimme käyttää seuraavaa ominaisuutta saadaksemme kunkin komponentin selittämän varianssin.
lda.explained_variance_ratio_
Aivan kuten aiemminkin, piirrämme kaksi LDA-komponenttia.
plt.xlabel('LD1')
plt.ylabel('LD2')plt.scatter(
X_lda,
X_lda,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Seuraavaksi tarkastellaan, miten LDA vertautuu pääkomponenttianalyysiin eli PCA:han. Aloitamme luomalla ja sovittamalla PCA-luokan instanssin.
from sklearn.decomposition import PCApca = PCA(n_components=2)X_pca = pca.fit_transform(X, y)
Voimme käyttää explained_variance_ratio_-ominaisuutta nähdäksemme kunkin komponentin selittämän varianssin prosenttiosuuden.
pca.explained_variance_ratio_
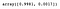
Kuten näemme, PCA valitsi ne komponentit, jotka johtaisivat suurimpaan hajontaan (säilyttäisivät suurimman osan informaatiosta), eikä välttämättä niitä, jotka maksimoivat luokkien välisen erottelun.
plt.xlabel('PC1')
plt.ylabel('PC2')plt.scatter(
X_pca,
X_pca,
c=y,
cmap='rainbow',
alpha=0.7,
edgecolors='b'
)

Katsotaan seuraavaksi, voimmeko luoda mallin luokitteluun käyttämällä LDA-komponentteja piirteinä. Ensin jaamme datan harjoittelu- ja testausjoukkoihin.
X_train, X_test, y_train, y_test = train_test_split(X_lda, y, random_state=1)
Sitten muodostamme ja harjoittelemme päätöspuun. Kun olemme ennustaneet testijoukon jokaisen näytteen luokan, luomme sekoitusmatriisin mallin suorituskyvyn arvioimiseksi.
dt = DecisionTreeClassifier()dt.fit(X_train, y_train)y_pred = dt.predict(X_test)confusion_matrix(y_test, y_pred)
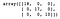
Kuten näemme, päätöspuu-luokittelija luokitteli kaikki testijoukon näytteet oikein.