Vad är cellmembranets permeabilitet?
Reader Mode
En av de utmärkande egenskaperna hos alla levande organismer är att de innehåller en distinkt blandning av joner och små molekyler. Sammansättningen skiljer sig inte bara från miljön utan kan också variera inom cellen. Till exempel kan koncentrationen av vätejoner i vissa cellutrymmen vara 104 gånger högre än i andra (mitokondrierna når ett pH så högt som 8; lysosomerna med ett pH så lågt som 4, BNID 107521, 106074). Förhållandet mellan koncentrationerna av Ca2+-joner i de extra- och intracellulära vätskekompartmenten kan återigen vara 104 gånger större (BNID 104083). Denna koncentrationsskillnad är så stor att det för att transportera en Ca2+-jon över membranet, från det intra- till det extracellulära kompartmentet, krävs energi från mer än en proton eller natriumjon som flödar nerför gradienten av proton-motivationskraft. För att se detta bör läsaren komma ihåg tumregeln från vår lista över knep som säger att det krävs 6 kJ/mol (≈2 kBT) för att upprätta en storleksordning av potentialskillnad. Denna energi kan uppnås till exempel genom transport av en elektrisk laddning genom en potentialskillnad på 60 mV. För att uppnå fyra storleksordningars koncentrationsförhållande skulle det då krävas att en laddning färdas nedåt med cirka 240 mV elektronmotivationskraft (i själva verket ännu mer på grund av kalciumjonens dubbla laddning). Detta är mycket nära membranets nedbrytningsspänning som diskuteras i vinjetten ”Vad är den elektriska potentialskillnaden över membran?”. Faktum är att det höga koncentrationsförhållandet för Ca2+ vanligtvis uppnås genom koppling till transporten av tre natriumjoner eller hydrolysen av ATP, vilket bidrar till att uppnå den erforderliga densitetsskillnaden utan att på ett farligt sätt ge energi till membranet.
Thermodynamikens andra lag lär oss att närvaron av koncentrationsgradienter i allmänhet så småningom kommer att blödas av genom masstransportprocesser, som stadigt driver systemen till ett tillstånd av jämvikt. Även om termodynamikens andra lag talar om karaktären av det slutliga tillståndet i ett system (t.ex. enhetliga koncentrationer) talar den emellertid inte om hur lång tid det tar att uppnå detta tillstånd. Membraner har utvecklats för att bilda en mycket effektiv barriär mot den spontana överföringen av många joniska och molekylära arter. För att uppskatta tidsskalan för att utjämna koncentrationerna måste vi känna till hastigheterna för masstransporten, som beror på viktiga materialegenskaper som diffusionskonstanter och permeabiliteter.
En enormt framgångsrik klass av ”lagar”, som beskriver beteendet hos system som har drabbats av någon liten avvikelse från jämvikten, är de linjära transportlagarna. Dessa lagar bygger på ett enkelt linjärt samband mellan transporthastigheten för en viss mängd av intresse och den tillhörande drivkraften. För masstransport finns det ett linjärt samband mellan flödet (dvs. antalet molekyler som korsar en areaenhet per tidsenhet) och koncentrationsskillnaden (som fungerar som den relevanta drivkraften). För transport genom membran har dessa idéer kodifierats i den enkla ekvationen (för en neutral lösta substans) j= – p-(cin-cout), där j är nettoflödet in i cellen, cin och cout avser koncentrationerna på insidan och utsidan av det membranbundna området, och p är en materialparameter som kallas permeabilitet. Enheterna för p kan härledas genom att notera att flödet har enheterna antal/(area x tid) och koncentrationen har enheterna antal/volym, vilket innebär att enheterna för p i sig är längd/tid. Liksom många transportmängder (t.ex. materialens elektriska ledningsförmåga som sträcker sig över 30 storleksordningar) har permeabiliteten ett mycket stort dynamiskt område, vilket illustreras i figur 1. Som framgår av figuren har lipidbilayers ett nästan 1010-faldigt intervall av permeabiliteter.
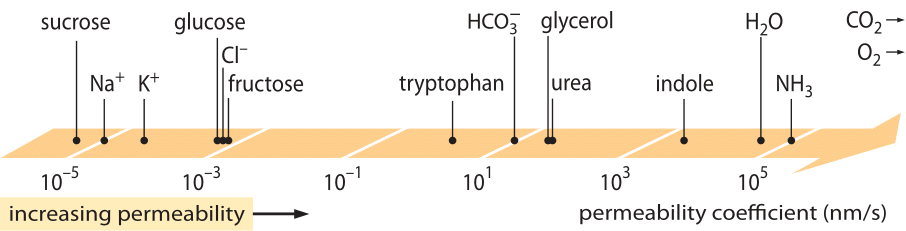
Figur 1: Det stora intervallet av membranpermeabiliteter för olika föreningar i cellen. Membranen är mer genomsläppliga för oladdade föreningar och minst genomsläppliga för laddade joner. Observera att förekomsten av jonkanaler gör att den synliga permeabiliteten när de är öppna blir flera storleksordningar högre. Enheterna har valts som nm/s och flera nm är den karakteristiska membranbredden. Figur anpassad från R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. Värdet för glukos är lägre än i Robertson baserat på flera källor, t.ex. BNID 110830, 110807. Andra datakällor: BNID 110729, 110731, 110816, 110824, 110806.
Vilka fysikalisk-kemiska parametrar styr placeringen av en förening på denna permeabilitetsskala? En tumregel är att små molekyler har högre permeabilitet än större molekyler. En annan tumregel är att neutrala föreningar kan passera membranet många storleksordningar snabbare än liknande laddade föreningar. Bland de laddade föreningarna tenderar negativa (anjoniska) föreningar att ha mycket högre permeabilitet än positiva (katjoniska) föreningar. Enligt den så kallade Overton-regeln ökar membranpermeabiliteten med hydrofobiciteten, där hydrofobiciteten är en förenings tendens att föredra ett opolärt lösningsmedel framför ett polärt (vattenhaltigt) lösningsmedel. Overtonregeln förutsäger att laddade molekyler (icke-hydrofoba), t.ex. joner, tenderar att ha en låg permeabilitet eftersom de får en energimässig påföljd i samband med att de tränger igenom membranet, medan upplösta gaser, t.ex. O2 och CO2, som är hydrofoba (eftersom de är oladdade och symmetriska), kommer att ha en hög permeabilitet. Permeabiliteten hos lipidbilagermembran för CO2 ger värden på 0,01-1 cm/s (ja, mätningar av permeabilitet har mycket stora osäkerheter mellan olika laboratorier, BNID 110004, 110617, 102624), vilket är högre än alla andra värden som visas i figur 1. Detta värde visar att den barriär som skapas av cellmembranet faktiskt är ett mindre hinder än den barriär som orsakas av det orörda vattenskiktet som uppslukar cellmembranet utifrån. En sådan slutsats kan härledas från ekvationen för ett hindrets permeabilitetskoefficient, som ges av p=K x D/l där l är bredden, D diffusionskoefficienten och K fördelningskoefficienten mellan medierna och hindrets material. Detta är också känt som ”löslighets-diffusions”-modellen för permeabilitet där dessa betecknar K- och D-effekterna som är två steg som påverkar permeabiliteten. För ett orörat vattenskikt är K=1 eftersom det är mycket likt media, men för membran är värdet för alla utom det mest hydrofoba materialet vanligen flera storleksordningar mindre än 1. Detta beroende av K är kärnan i den Overton-regel som nämns ovan. Den höga permeabiliteten för koldioxid tyder också på att kanaler som akvaporiner, som föreslogs användas för gastransport in i cellen, inte behövs eftersom membranet är tillräckligt genomsläppligt. För att se hur membranegenskaperna påverkar metaboliternas kemiska sammansättning vänder vi oss till att beräkna läckagetiden för olika föreningar
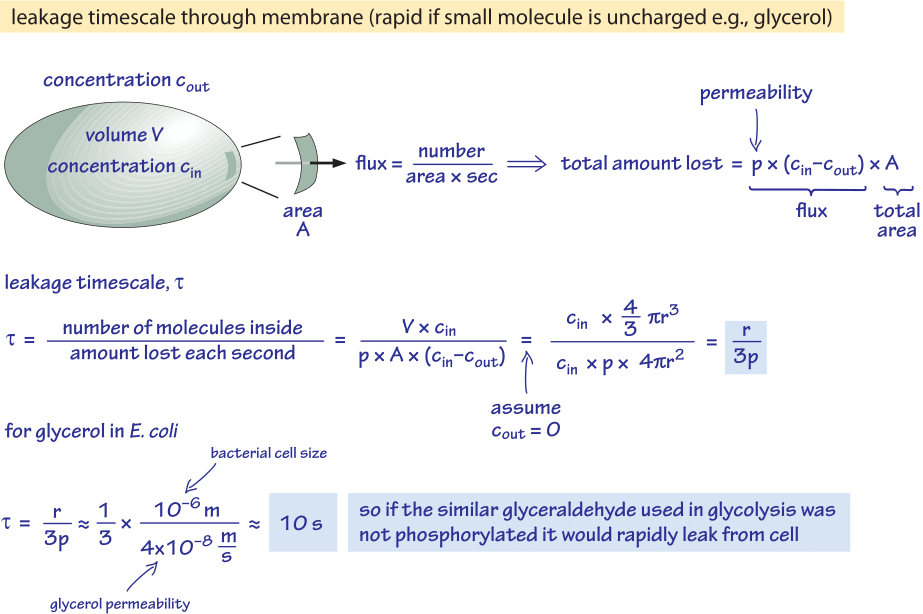
Figur 2: Back of the envelope-beräkning av tidsskalan för ofosforylerad glukosmolekyl att passivt diffundera ut ur en bakteriecell. De funktionella konsekvenserna beaktas sedan för snabbt växande celler där effekten är försumbar och för celler i stationärt tillstånd där den kan orsaka ett märkbart läckage av resurser.
Vi betraktar till exempel glycerol. Analysen i figur 2 ger en uppskattning av tiden för dess läckage ut ur cellen om molekylen inte fosforyleras eller på annat sätt omvandlas till en mer hydrofil form. Cellmembranets permeabilitet för glycerol är p≈10-100 nm/s (BNID 110824), vilket kan utläsas av figur 1. Tidsskalan för en glycerolmolekyl inne i cellen att flyta tillbaka till det omgivande mediet, om man antar att det inte finns något returflöde in i cellen (cout=0), kan grovt uppskattas genom att notera att utflödet från cellen är p-A-cin där A är cellytan. Tidsskalan hittas genom att ta den totala mängden i cellen, V-cin (där V är cellvolymen eller mer exakt cellvattenvolymen), och dividera med detta flöde vilket för en bakteriecell (r≈1 μm) resulterar i en tidsskala:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Detta är en grov uppskattning eftersom vi inte tog hänsyn till den minskande koncentrationen av cin med tiden som ger en korrigeringsfaktor på 1/ln(2), dvs. mindre än 2-faldig ökning. Vad vi lär oss av dessa uppskattningar är att om de glykolytiska mellanprodukterna glyceraldehyd eller dihydroxyaceton, som är mycket lika glycerol, inte fosforylerades, vilket resulterar i att en laddning läggs till, skulle de gå förlorade till mediet genom diffusion genom cellmembranet. I laboratoriemedier, där en kolkälla tillförs i överflöd, är detta inget större problem, men i en naturlig miljö där cellerna ofta väntar i stationär fas på en lycklig puls av näringsämnen (E. coli tros gå igenom månader utan tillväxt efter att den har utsöndrats från kroppen innan den hittar en ny värd), kan cellen begränsa sina förluster genom att se till att metaboliska intermediärer förses med en laddning som hindrar dem från att korsa den barriär som lipiddubbelskiktet utgör.




