Punktsymmetri föreligger när figuren ritas runt en enda punkt.

Denna punkt kallas figurens centrum eller symmetrins centrum. I den intilliggande figuren ser vi att motsvarande punkten X på figuren finns det en punkt X’ på andra sidan centrum som är direkt motsatt X och ligger på figuren. Vi säger att figuren är symmetrisk kring centrum.
Note:
När vi roterar en figur om 180° och den återfår sin ursprungliga form, säger vi att det finns punktsymmetri i figuren.
Exempel på figurer som uppvisar punktsymmetri:
● Alla bokstäver i det engelska alfabetet.
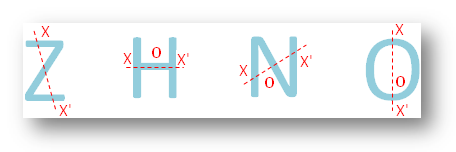
● Olikageometriska figurer.
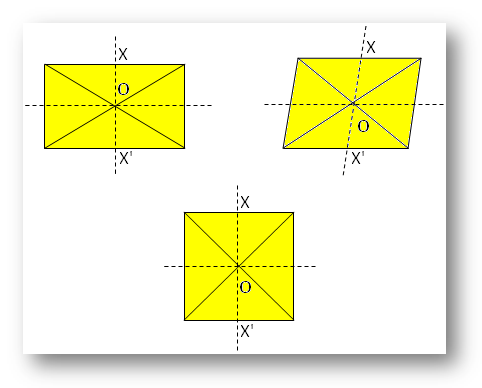
Note:
Här är O symmetricentrum.
Med avseende på X finns det X’, så att X’ är direkt motsatt till X på andra sidan av O.
Vilka villkor uppfyller en form eller en figur för punktsymmetri?
Villkoren som en form eller en figur uppfyller för punktsymmetri är att varje del ska ha en matchande del
– avståndet ska vara lika långt från den centrala punkten
– men ska vara i motsatt riktning.
● Relaterade begrepp
● Linjär symmetri
● Symmetrilinjer
● Rotationssymmetri
● Rotationssymmetrins ordning
● Typer av symmetri
● Spegling
● Spegling av en punkt i x-.axel
● Reflektion av en punkt i y-axeln
● Reflektion av en punkt i y-axelnaxel
● Spegling av en punkt i ursprunget
● Rotation
● 90 graders rotation medurs
● 90 graders rotation moturs
● 180 graders rotation
● 180 graders rotation
Matematiska problem i sjunde klass
Matematiska övningar i åttonde klass
Från punktsymmetri till HEMSIDESIDAN