Pearson Mode Skewness

Statistikdefinitioner >Pearson Mode Skewness

Pearson Mode Skewness, som också kallas Pearsons första skevhetskoefficient, är ett sätt att räkna ut skevheten i en fördelning.

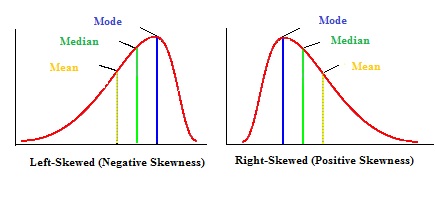
Medelvärdet, läget och medianen kan användas för att ta reda på om man har en positivt eller negativt skev fördelning.

• Om medelvärdet är större än modus är fördelningen positivt skev.
• Om medelvärdet är mindre än modus är fördelningen negativt skev.
• Om medelvärdet är större än medianen är fördelningen positivt skev.
• Om medelvärdet är mindre än medianen är fördelningen negativt skev.

Pearson Mode skewness

Pearson mode skewness använder ovanstående fakta för att hjälpa dig att ta reda på om du har positiv eller negativ skewness. Om du har en fördelning och känner till medelvärde, läge och standardavvikelse (σ) är formeln för Pearson mode skewness:

(medelvärde-läge)/σ

Problem: Du har data med ett medelvärde på 19, ett läge på 20 och en standardavvikelse på 25. Vad säger Pearson Mode Skewness om fördelningen?
(mean-mode)/σ = (19-20)/25 = -0,04.
Det finns en mycket liten negativ skewness (-0,04). Anmärkning: För de flesta ändamål skulle detta räknas som en symmetrisk fördelning eftersom skevheten är så liten.

Pearson Mode Skewness: Alternativ formel.

Om du inte känner till läget kan du inte använda Pearson mode skewness. Men man kan också räkna ut riktningen på skewness genom att ta reda på var medelvärdet och medianen ligger. Enligt Business Statistics leder detta till en andra, likvärdig formel:

3(Medelvärde – Median) / σ

Denna formel kallas också Pearsons andra skewnesskoefficient.

Pearson Mode Skewness:

Den skillnad som finns mellan medelvärde och modus, eller medelvärde och median, visar hur mycket fördelningen avviker från symmetrin. En symmetrisk fördelning (till exempel normalfördelningen) har en skewness på noll.
Båda ekvationerna ger dig resultat i standardavvikelser, som är dimensionslösa måttenheter från medelvärdet.

Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Vogt, W.P. (2005). Ordbok över statistik & Metodik: A Nontechnical Guide for the Social Sciences. SAGE.

——————————————————————————

Har du behov av hjälp med en läxa eller en provfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert inom området. Dina första 30 minuter med en Chegg-handledare är gratis!