Innan vi börjar måste vi göra några antaganden.
För det första arbetar vi med newtonska vätskor. Detta är det enklaste matematiska sättet att redogöra för viskositeten i en vätska. Det finns inga verkliga vätskor som helt och hållet faller under denna kategori, men i de flesta fall kan luft och vatten behandlas som en newtonsk vätska. Den andra mycket viktiga hypotesen vi gör är att vätskan är inkompressibel. Detta innebär att dess densitet, rho, är en konstant.
Massans bevarande
Den första ekvationen talar om att massan av den vätska vi arbetar med är bevarad. Vätskan kan ändra sin form men den här ekvationen säger oss att massan är densamma från början till slut.
Nu ska vi prata matematik. Bokstaven u representerar vätskans hastighet och är en vektor. Den har tre komponenter, vi kan kalla dem u, v, w och de representerar vätskans hastighet i x-, y- och z-riktningen. Den grekiska bokstaven nabla ∇ följt av en punkt är divergensoperatorn. Det innebär att vi måste differentiera dess komponenter i varje riktning (i det här fallet x, y, z).

Den första derivatan talar om hur x-komponenten av hastigheten förändras när vi rör oss i x-ledet. Samma sak gäller för de andra två derivatorerna. Eftersom den här ekvationen är lika med noll visar den oss att massan är bevarad.
Momentets bevarande

Den andra ekvationen är egentligen en uppsättning av tre differentialekvationer. Det är den som kan beskrivas som Newtons andra lag för vätskorna. Om vi expanderar uttrycket får vi ett komplext system.
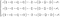
Då det är mycket enklare att förstå kommer vi att koncentrera oss på momentbevarandet inte expanderat.
När vi arbetar med vätskor kan vi säga att massa och densitet är samma sak (så länge deras volym är densamma). Om vi betraktar två vätskor kan vi säga att den tätare är den ”tyngre” (t.ex. kvicksilver och vatten). I detta fall är den grekiska bokstaven ρ (rho) vätskans densitet.
Vi har massan, för att återgå till Newtons andra lag behöver vi nu accelerationen. Det är exakt resultatet av tidsderivatan av hastighetsvektorn.

Nu återstår bara termerna till höger om likhetstecknet, och de representerar alla de krafter som appliceras på vätskan.
Den första termen ∇p är gradienten för trycket. Den representerar skillnaden i tryck i det utrymme där vätskan finns. Om det till exempel finns en zon med lågt tryck och en annan med högre tryck kommer vätskan att röra sig från högtrycksavsnittet till det lägre. Gradienten för p säger allt detta.
Den andra termen beskriver vätskans viskositet. Tänk på två olika vätskor, som vatten och honung. När du häller upp ett glas vatten faller det snabbt och lätt. När du gör samma sak med honung är den klibbig och den häller mycket långsamt. Detta är vad uttrycket säger.
Den sista termen, F, är den enklaste eftersom den representerar alla yttre krafter som kan appliceras på denna vätska. Vanligtvis är den kraft vi betraktar här gravitationen.
Det här är det, alla dessa tjusiga symboler och bokstavsbetydelse är bara kraft = massa x acceleration.
Användning av Navier-Stokes ekvationer
Då det är så komplicerat att lösa dessa ekvationer, för att kunna använda dem måste vi göra en massa approximationer. Några exempel är Poiseuille- och Couetteflödet. Med många antaganden kunde dessa två forskare hitta en lösning på Navier-Stokes ekvationer för en mycket specifik tillämpning. Men om vi vill använda dem för en mer komplicerad uppgift, som väderprognoser, måste vi göra något annat.
Det vanligaste sättet att använda dessa ekvationer är att omvandla dem, med Reynolds medelvärde. Detta är en avancerad matematisk process och resultatet är Reynolds ekvationer. De brukar kallas RANS-ekvationer (vilket betyder Reynolds averageed Navier-Stokes).
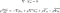
De här ekvationerna används när fluiden befinner sig i ett turbulent flöde. De ser nästan exakt ut som Navier-Stokes ekvationer, förutom den sista termen. Denna kallas Reynolds spänningstenor. Det är den kvantitet som gör att vi kan ta hänsyn till turbulensen i vätskan.
I RANS-ekvationerna medelvärdesberäknas de kvantiteter som vi använder över ett tidsintervall. Detta intervall måste vara tillräckligt litet för att möjliggöra observation av det fenomen vi studerar. Samtidigt måste det vara tillräckligt stort för att turbulensverkan ska förlora betydelse.
Med rätt antaganden fungerar dessa ekvationer. Vi vet hur vi kan använda dem för att göra F1-bilarna snabbare, för att få en rymdfarkost att åka till ISS och för att göra väderprognoser. Så du kanske undrar varför beviset för dessa ekvationer är värt en miljon dollar?
En miljon dollar i pris
Från fysikens synvinkel är dessa ekvationer bara Newtons andra lag som fungerar med vätskor. När vi gör vissa antaganden och förenklingar kan vi göra fantastiska saker med dem.
Det verkliga problemet är detta. Att lösa dessa ekvationer utan approximationer är helt enkelt fruktansvärt komplicerat. Det är så svårt att det inte har bevisats att lösningarna faktiskt existerar. Och det är här millenniepriset kommer in.
Den officiella problemformuleringen (du hittar den här) är:
Bevisa eller ge ett motexempel till följande påstående: i tre rumsdimensioner och tid, givet ett initialt hastighetsfält, finns det en vektorhastighet och ett skalärt tryckfält, som båda är jämna och globalt definierade, som löser Navier-Stokes-ekvationerna.
Vad detta innebär är att för att vinna priset måste man göra tre saker:
- Bevisa att en lösning existerar
- Lösningen måste existera i varje punkt i rymden
- Lösningen måste vara jämn. Detta innebär att en liten förändring av de ursprungliga förhållandena ger endast en liten variation av resultatet.
För en ingenjör räcker det vanligtvis med att veta att dessa ekvationer fungerar, även om det bara är till en viss grad av approximation. Men för en matematiker är det mycket viktigt att veta om lösningarna finns och hur de beter sig.
Du kanske nu tänker att om ekvationerna fungerar som de gör, är det ett totalt slöseri med tid och energi att leta efter ett bevis. Tja, liksom många tekniska framsteg i mänsklighetens historia kan resultatet kanske inte tyckas särskilt viktigt. Det viktiga är vägen dit, som kan ge ny kunskap och förbättringar i vårt liv.
Tänk på rymduppdrag. Om människan aldrig hade bestämt sig för att åka och gå på månen skulle vi inte ha många föremål som används för att förbättra vårt liv. MRI-maskiner och pacemakers kommer från teknik som utvecklats för rymdforskning. I dag använder läkare över hela världen dem varje dag för att rädda liv. Samma sak gäller här. Vägen till att upptäcka lösningen på Navier-Stokes ekvationer kommer att hjälpa oss att förbättra vår förståelse av vätskor med mera. Det kan leda oss till nya upptäckter och kommer förmodligen att kräva att vi uppfinner ny matematik. Detta kan sedan användas för att besvara många andra problem, för att uppfinna ny teknik för att förbättra våra liv och göra oss bättre.