Vi kommer att beskriva tre exempel från livsvetenskaperna: ett från fysik, ett från genetik och ett från ett musförsök. De är mycket olika, men ändå slutar vi med att använda samma statistiska teknik: anpassning av linjära modeller. Linjära modeller lärs vanligtvis ut och beskrivs med hjälp av språket matrisalgebra.
Motiverande exempel
Fallande föremål
Föreställ dig att du är Galileo på 1500-talet som försöker beskriva hastigheten hos ett fallande föremål. En assistent klättrar upp i Pisa-tornet och släpper en kula, medan flera andra assistenter registrerar positionen vid olika tidpunkter. Låt oss simulera några data med hjälp av de ekvationer vi känner till idag och lägga till lite mätfel:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersAssistenterna överlämnar data till Galileo och det här är vad han ser:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")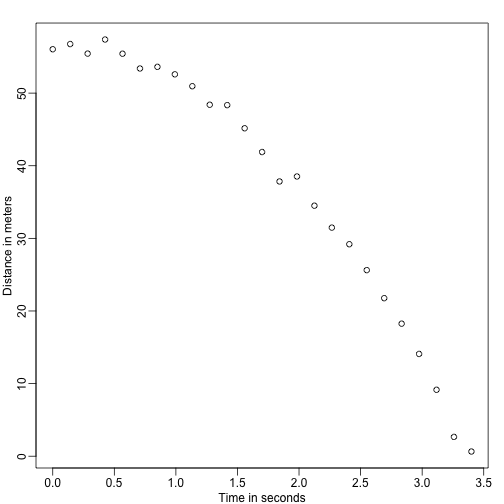
Han känner inte till den exakta ekvationen, men genom att titta på grafen ovan drar han slutsatsen att positionen bör följa en parabel. Så han modellerar data med:
Med representerar platsen, representerar tiden och tar hänsyn till mätfel. Detta är en linjär modell eftersom det är en linjär kombination av kända storheter (th s) som kallas prediktorer eller kovarianter och okända parametrar (the s).
Fadern & sonens höjder
Föreställ dig nu att du är Francis Galton på 1800-talet och att du samlar in parvisa höjddata från fäder och söner. Du misstänker att längd ärvs. Dina data:
library(UsingR)x=father.son$fheighty=father.son$sheightser ut så här:
plot(x,y,xlab="Father's height",ylab="Son's height")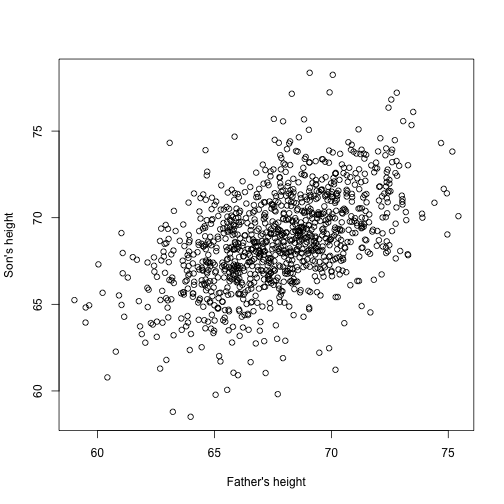
Sönernas höjd tycks faktiskt öka linjärt med fädernas höjd. I detta fall är en modell som beskriver data följande:
Det här är också en linjär modell med och , faderns respektive sonens höjd för det -te paret och en term för att ta hänsyn till den extra variabiliteten. Här tänker vi oss att fädernas höjder är prediktorerna och att de är fasta (inte slumpmässiga) så vi använder små bokstäver. Enbart mätfel kan inte förklara all den variabilitet som ses i . Detta är logiskt eftersom det finns andra variabler som inte ingår i modellen, t.ex. mödrarnas höjder, genetisk slumpmässighet och miljöfaktorer.
Slumpmässiga prover från flera populationer
Här läser vi in data om musars kroppsvikt från möss som utfodrades med två olika dieter: hög fetthalt och kontroll (chow). Vi har ett slumpmässigt urval på 12 möss för vardera. Vi är intresserade av att fastställa om dieten har en effekt på vikten. Här är data:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")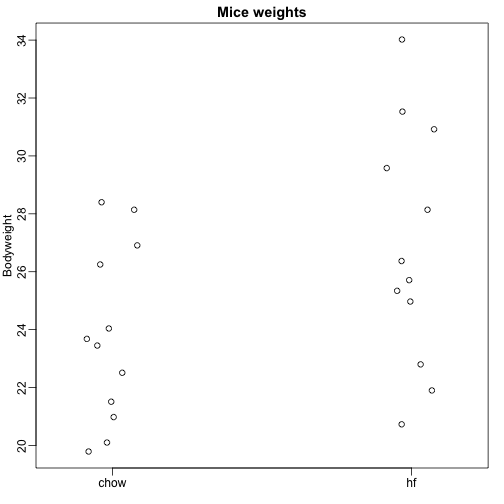
Vi vill uppskatta skillnaden i genomsnittlig vikt mellan populationerna. Vi visade hur man gör detta med hjälp av t-test och konfidensintervall, baserat på skillnaden i stickprovsgenomsnitt. Vi kan få exakt samma resultat med hjälp av en linjär modell:
med chowdietens medelvikt, skillnaden mellan medelvärdena, när musen får högfettdiet (hf), när den får chowdiet, och förklarar skillnaderna mellan möss i samma population.
Linjära modeller generellt
Vi har sett tre mycket olika exempel där linjära modeller kan användas. En allmän modell som omfattar alla ovanstående exempel är följande:
Bemärk att vi har ett allmänt antal prediktorer . Matrisalgebra ger ett kompakt språk och ett matematiskt ramverk för att beräkna och göra härledningar med alla linjära modeller som passar in i ovanstående ramverk.
Skattning av parametrar
För att modellerna ovan ska vara användbara måste vi skatta de okända s. I det första exemplet vill vi beskriva en fysikalisk process för vilken vi inte kan ha okända parametrar. I det andra exemplet förstår vi bättre arv genom att uppskatta hur mycket, i genomsnitt, faderns längd påverkar sonens längd. I det sista exemplet vill vi avgöra om det faktiskt finns en skillnad: om .
Standardmetoden inom vetenskapen är att hitta de värden som minimerar avståndet mellan den anpassade modellen och data. Följande kallas ekvationen för minsta kvadraters (LS) ekvation och vi kommer att se den ofta i det här kapitlet:
När vi har hittat miniminivån kallar vi värdena för minsta kvadraters skattningar (LSE) och betecknar dem med . Den kvantitet som erhålls när man utvärderar ekvationen för de minsta kvadraterna vid skattningarna kallas residual sum of squares (RSS). Eftersom alla dessa kvantiteter beror på , är de slumpmässiga variabler. S är slumpvariabler och vi kommer så småningom att utföra inferenser på dem.
Exemplet med det fallande föremålet återupptaget
Tack vare min fysiklärare på gymnasiet vet jag att ekvationen för ett fallande föremåls bana är:
med och utgångshöjd respektive utgångshastighet. De data vi simulerade ovan följde denna ekvation och lade till mätfel för att simulera n observationer för att släppa bollen från Pisa-tornet . Därför använde vi den här koden för att simulera data:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Här ser data ut med den heldragna linjen som representerar den sanna banan:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)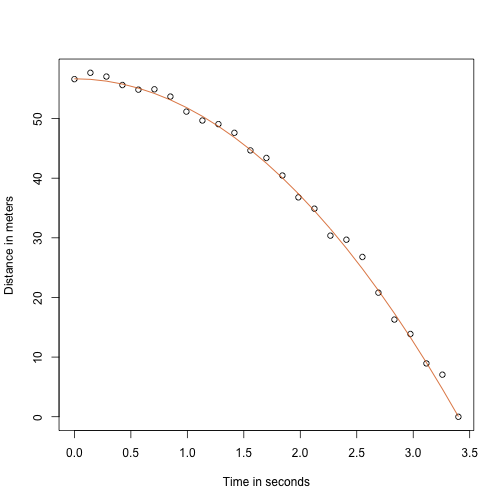
Men vi låtsades vara Galileo och därför känner vi inte till parametrarna i modellen. Data tyder på att det är en parabel, så vi modellerar den som en sådan:
Hur hittar vi LSE?
Funktionen lm
I R kan vi anpassa den här modellen genom att helt enkelt använda funktionen lm. Vi kommer att beskriva denna funktion i detalj senare, men här är en förhandsvisning:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Den ger oss LSE, samt standardfel och p-värden.
En del av det vi gör i det här avsnittet är att förklara matematiken bakom denna funktion.
Skattningen av de minsta kvadraterna (LSE)
Låt oss skriva en funktion som beräknar RSS för vilken vektor som helst :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Så för vilken tredimensionell vektor som helst får vi en RSS. Här är en plott av RSS som en funktion av när vi håller de andra två fixerade:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)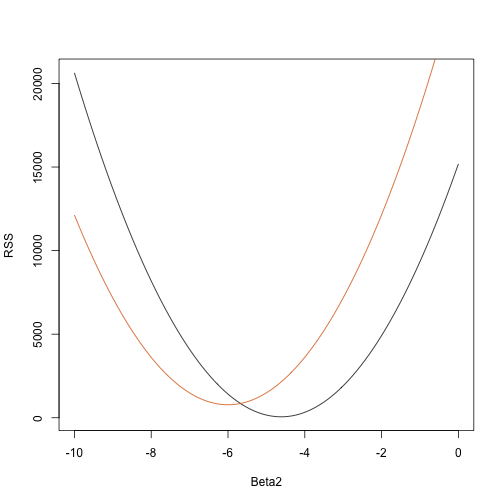
Trial and error här kommer inte att fungera. Istället kan vi använda kalkyl: ta de partiella derivatorerna, sätt dem till 0 och lös dem. Om vi har många parametrar kan dessa ekvationer naturligtvis bli ganska komplexa. Linjär algebra ger ett kompakt och generellt sätt att lösa detta problem.
Mer om Galton (Avancerat)
När Galton studerade uppgifterna om far och son gjorde han en fascinerande upptäckt med hjälp av explorativ analys.
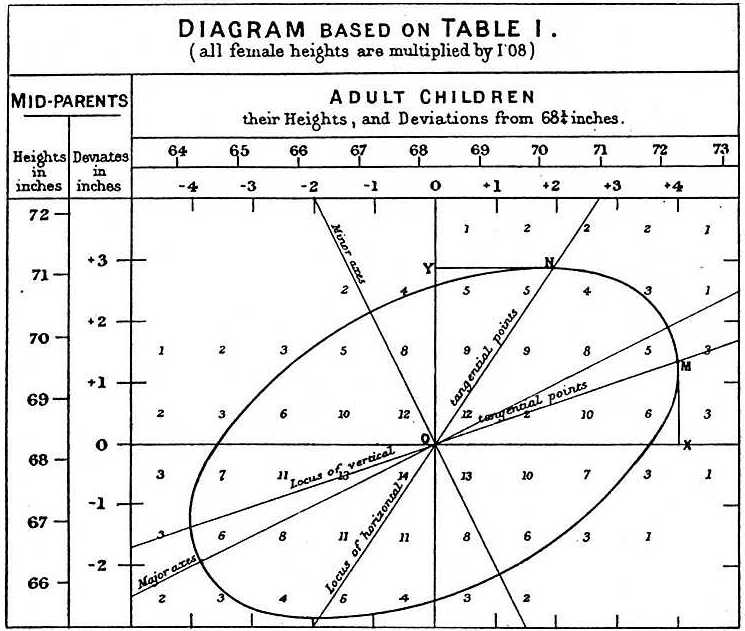
Han noterade att om han tabellerade antalet längdpar mellan far och son och följde alla x,y-värden som hade samma totaler i tabellen, så bildade de en ellips. I diagrammet ovan, som Galton gjort, ser man ellipsen som bildas av de par som har 3 fall. Detta ledde sedan till att modellera dessa data som korrelerade bivariata normala som vi beskrev tidigare:
Vi beskrev hur vi kan använda matematik för att visa att om man håller fast (villkoret att vara ) så är fördelningen av normalfördelad med medelvärde: och standardavvikelse . Observera att är korrelationen mellan och , vilket innebär att om vi fixerar , följer faktiskt en linjär modell. Parametrarna och i vår enkla linjära modell kan uttryckas i termer av , och .