 |
Liksidig triangel |
|
Vi kommer att göra TRE konstruktioner av en liksidig triangel. Den första kommer att vara att konstruera en liksidig triangel med en sidas längd, och de andra två kommer att vara att konstruera en liksidig triangel inskriven i en cirkel.
|
Givet: längden på triangelns ena sida
Konstruera: en liksidig triangel |
 |
STEG:
1. Placera kompasspunkten på A och mät avståndet till punkt B. Svinga en båge av denna storlek över (eller under) segmentet.
2. Utan att ändra kompassens spännvidd placerar du kompasspunkten på B och svänger samma båge som skär den första bågen.
3. Märk skärningspunkten som den liksidiga triangelns tredje hörn.
 |
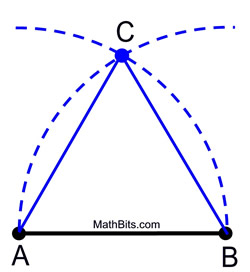Se de fulla cirklarna i arbete.
 |
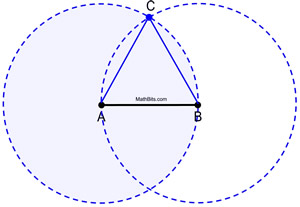Bevis för konstruktionen: Cirkel A är kongruent med cirkel B, eftersom de båda bildades med samma radie, AB. Eftersom AB och AC är längder på radierna i cirkel A är de lika långa som varandra. På samma sätt är AB och BC radier i cirkel B lika långa som varandra. Därför är AB = AC = BC genom substitution (eller transitiv egenskap). Eftersom kongruenta segment har samma längd, 
och ΔABC är liksidig (har tre kongruenta sidor).
|
Givet: en bit papper
Konstruera: en liksidig triangel inskriven i en cirkel. |
Detta är en modifiering av konstruktionen av en regelbunden hexagon inskriven i en cirkel.
|
STEG:
1. Placera din kompasspunkt på pappret och rita en cirkel. (Behåll detta kompassspann!)
2. Placera en punkt, märkt A, var som helst på cirkelns omkrets för att fungera som en startpunkt.
3. Utan att ändra kompassens spännvidd placerar du kompasspunkten på A och svänger en liten båge som korsar cirkelns omkrets.
4. Utan att ändra kompassens spännvidd flyttar du kompasspunkten till skärningspunkten mellan den föregående bågen och omkretsen och gör ytterligare en liten båge på cirkelns omkrets.
5. Fortsätt att upprepa denna process med att ”kliva” runt cirkeln tills du återvänder till punkt A.
6. Börja vid A och anslut varannan båge på cirkeln för att bilda den liksidiga triangeln.
 |
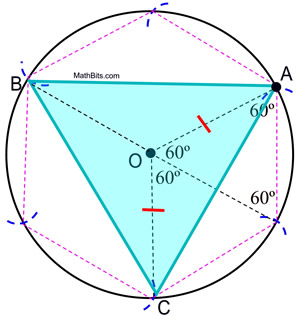Se beviset för en inskriven regelbunden hexagon för mer information om beviset för denna konstruktion.
|
Bevis för konstruktionen: Beviset för en inskriven regelbunden hexagon visar att de centrala vinklarna i en regelbunden hexagon innehåller 60º. De centrala vinklarna i den triangel som är inskriven i denna cirkel innehåller 120º. Eftersom ΔAOC är likbent (OA och OC är radiernas längder) är m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC 
ΔCOB ΔBOA enligt SAS. Enligt CPCTC är ∠OCB ∠OCA och m∠OCB = 30º genom substitution och m∠BCA = 60º. På liknande sätt har vi m∠ACB = m∠CBA = m∠BAC = 60º och liksidig ΔABC.
|
Givet: en bit papper
Konstruera: en liksidig triangel inskriven i en cirkel. |
Denna metod använder kunskap om den speciella rätvinkliga triangeln 30º – 60º – 90º.
|
STEG:
1. Placera kompasspunkten på pappret och rita en cirkel, O. (Behåll kompassens spännvidd!)
2. Rita en diameter av cirkeln med hjälp av ett linjal och märk ändpunkterna P och B.
3. Utan att ändra kompassens spännvidd placerar du kompasspunkten på P och ritar en hel cirkel.
4. Märk skärningspunkterna mellan de två cirkelomkretsarna med A och C.
5. Rita segment från A till B, B till C och C till A för att bilda den liksidiga triangeln.
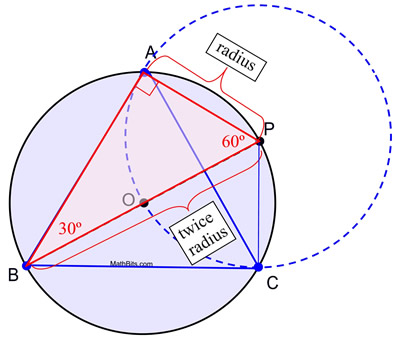
Bevis för konstruktionen: Denna konstruktion använder det faktum att en vinkel som är inskriven i en halvcirkel är en rät vinkel, och att i en 30º-60º-90º triangel är längden på det korta benet hälften av längden på hypotenusan. I denna konstruktion är cirkel O och cirkel P kongruenta eftersom de har samma radie. AP är en radie av cirkel P och radierna AP = OP. OP är också en radie i cirkel O (tillsammans med OB) och diametern BP = BO + OP = 2 OP. Genom substitution blir BP = 2 AP, vilket skapar de nödvändiga villkoren för att m∠ABP = 30º. Följaktligen är m∠APB = 60º. Ett liknande argument kan användas för att fastställa att för ΔPBC, m∠PBC = 30º och m∠BPC = 60º vilket gör att ΔPBC ΔPBA med ASA (med gemensam sida från B till P).
Nu, 
eftersom de är motsvarande sidor i de två kongruenta trianglarna, vilket gör att ΔABC är likbent. ∠BAC ∠BCA eftersom basvinklarna i en liksidig triangel är kongruenta.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º genom vinkeladditionspostulat och substitution. m∠BAC + m∠BCA + m∠ABC = 180º eftersom summan av vinkelmåtten i en triangel är 180º. Eftersom m∠BAC + m∠BAC + 60º = 180º genom substitution vet vi att 2m∠BAC = 120º och m∠BAC = 60º. Följaktligen är m∠BCA också lika med 60º genom substitution, vilket gör ΔABC liksidigt.
