Introduktion av Klein-flaskan

Om du gillar att dricka är en Klein-flaska inte en rekommenderad behållare. Den kan se vagt ut som en flaska, men den innesluter ingen volym, vilket innebär att den faktiskt inte kan innehålla någon vätska. Vad du än häller ”i” kommer bara att komma ut igen.

Hur konstruerar man en sådan konstig sak och varför skulle man vilja konstruera den? Matematikern Felix Klein, som upptäckte flaskan 1882, beskrev den som en yta som ”kan visualiseras genom att vända en bit av en gummislang och låta den passera genom sig själv så att utsidan och insidan möts”.

Din webbläsare stöder inte videotaggen.Direktlänk

Det är uppenbart att Klein-flaskan, precis som den mer välkända sfären, är en sluten yta: den är ändlig i den bemärkelsen att man kan få plats med den i ett begränsat område av utrymmet, men en myra skulle kunna gå runt på den i all evighet utan att någonsin stöta på en gräns eller falla över en kant. Till skillnad från klotet, som har en insida och en utsida, är Klein-flaskan ensidig: när vår myra går runt kan den nå båda sidorna av varje punkt på ytan. Detta är anledningen till att flaskan inte innesluter någon volym, och det svarar också på frågan ”varför”: Klein-flaskan är intressant eftersom vi inte stöter på många ensidiga former i naturen. (Se här för en annan mycket vacker bild på en Klein-flaska.)

Möbiusbandet är ensidigt – se den animerade versionen. (Bild och animation av Konrad Polthier.)

Om detta är lite förvirrande kan du tänka på ett enklare exempel på en ensidig yta: den berömda Möbiusremsan. Du kan göra en sådan genom att ta två ändar av en pappersremsa, ge remsan en vridning och sedan limma ihop ändarna. Genom att använda en pappersremsa vars två sidor har olika färger, till exempel grön och orange, är det lätt att övertyga sig själv om att den resulterande Möbiusremsan är ensidig. När du väl har vridit och limmat kommer du att upptäcka att du kan nå varje orange punkt från varje grön punkt utan att behöva gå igenom pappret eller klättra över dess kant.

I motsats till Klein-flaskan har Möbiusremsan en gräns – den utgörs av de två icke limmade kanterna på den ursprungliga remsan. Men det finns en länk mellan de två. Om man tar två Möbiusremsor och skapar en sluten form genom att sammanfoga deras gränser med hjälp av en vanlig tvåsidig remsa, som visas nedan, är det man får exakt Klein-flaskan.

Din webbläsare har inte stöd för videotaggen Direktlänk

Detta faktum inspirerade matematikern Leo Moser att komponera en limerick:

En matematiker vid namn KleinTänkte att Möbiusbandet var gudomligt.Said he: ”Om du limmar ihop kanterna av två, får du en konstig flaska som min.”

Vissa matematiker är verkligen mångsidiga!

En annan märklig egenskap hos Klein-flaskan är att den skär sig själv, vilket innebär att det är svårt att tillverka den av ett enda gummirör, som Klein föreslog. Strängt taget är det självskärande objektet som avbildas ovan inte en Klein-flaska, utan (som Klein angav) endast en visualisering av en sådan. För att förstå varför, tänk först på den mer välkända munken (matematiskt känd som en torus). Man kan göra en torus av en fyrkantig gummiplåt genom att först limma ihop två motsatta sidor för att bilda en cylinder och sedan limma ihop de två gränskomponenterna av den cylindern för att få torusen.

För att göra en torus: Först limmar man motsatta punkter på två motsatta sidor av kvadraten för att få en cylinder och sedan limmar man de två gränskretsarna av den cylindern (vilket motsvarar att man limmar motsatta punkter på de återstående två sidorna av kvadraten) för att få en torus.

Om man inte vill bry sig om limningen kan man helt enkelt tänka sig torusen som en kvadrat, med tanke på att motsatta punkter på motsatta sidor betraktas som samma sak. Så när du för en form som ritats på ”kvadraten” över den övre kanten kommer den att dyka upp igen vid den nedre kanten och när du för den över den högra kanten kommer den att dyka upp igen vid den vänstra kanten (och vice versa).

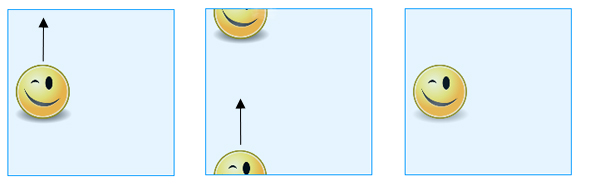
När du drar en form som ritats på ”kvadraten” över den övre kanten kommer den att dyka upp igen vid den nedre kanten.

För att få fram en riktig Klein-flaska börjar du på samma sätt, genom att identifiera motsatta punkter på ett par motsatta sidor av en kvadrat. För det andra paret av sidor ska du dock inte identifiera punkter som är direkt motsatta, utan punkter som är diagonalt motsatta, enligt bilden.

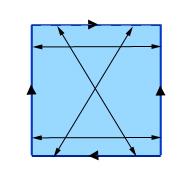
Bygg en Klein-flaska: Identifiera motsatta punkter på två motsatta sidor (de vertikala på bilden) och identifiera sedan diagonalt motsatta punkter på de återstående två sidorna. (Om du märker punkterna på över- och undersidan från vänster till höger med siffrorna 0 till 1, så identifieras en punkt med etiketten x på ovansidan med punkten med etiketten 1-x på undersidan.)

Det resulterande föremålet är Klein-flaskan. Återigen kan du tänka på den som en kvadrat, med tanke på vilka gränspunkter som betraktas som samma. Om du för en form över en av de kanter som hade motsatta punkter identifierade (vertikal i vår bild), så dyker den upp igen dyker upp igen på den motsatta sidan, som tidigare. Om du däremot för den över en av de kanter vars punkter identifierades diagonalt (horisontellt i vår bild), dyker den upp på motsatt sida, men förskjuten och som en spegelbild av sitt ursprungliga jag.

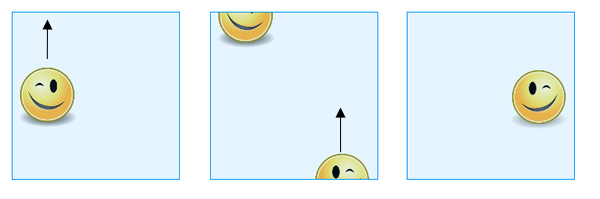
Om du glider en form över den övre kanten visas den över den nedre kanten, men över till andra sidan och som en spegelbild av sitt ursprungliga jag.

Det enda sättet att bygga upp den här formen i det tredimensionella rummet genom att faktiskt limma ihop punkter är att låta den korsa sig själv. Detta går ut på att identifiera punktpar i den ursprungliga fyrkantens inre, så strängt taget är den resulterande formen inte exakt densamma som Klein-flaskan, för vilken endast gränspunkter har identifierats. Det är bara ett sätt att representera flaskan i det tredimensionella rummet (det finns också andra).

Märkligt nog beror begreppen ”inne”, ”ute” och ”ensidighet” på det omgivande rummet som ett objekt befinner sig i. Till exempel har en slinga som ritas på ett papper (i ett tvådimensionellt rum) en väldefinierad insida och utsida, men en slinga som ritas i ett tredimensionellt rum har inte det. Det är därför vi inte kan tala om ensidighet om vi inte först bestämmer oss för hur en yta ska inbäddas i ett tredimensionellt rum. Det finns dock en närbesläktad egenskap som är inneboende i en form och som inte är beroende av det omgivande rummet. En yta kallas orienterbar om man inte kan glida en form som ritats på den runt och tillbaka till utgångspunkten så att den ser ut som sin egen spegelbild. Som du kan se i animationen som åtföljer bilden till höger är Möbiusremsan inte orienterbar. Och som du kan se på bilden med smiley-ansiktet ovan ovan är inte heller Klein-flaskan det.För att ge den sin fullständiga matematiska beskrivning är Klein-flaskan en sluten, icke-orienterbar yta. Om du vill veta mer om den kan du läsa artikeln Inside the Klein bottle.

Om författaren

Marianne Freiberger är redaktör för Plus.