Publicerat den 27 augusti 2015
Recurrent Neural Networks
Människor börjar inte tänka från början varje sekund. När du läser den här uppsatsen förstår du varje ord utifrån din förståelse av tidigare ord. Du kastar inte bort allting och börjar tänka från början igen. Dina tankar har uthållighet.
Traditionella neurala nätverk kan inte göra detta, och det verkar vara en stor brist. Tänk dig till exempel att du vill klassificera vilken typ av händelse som sker vid varje tidpunkt i en film. Det är oklart hur ett traditionellt neuralt nätverk skulle kunna använda sitt resonemang om tidigare händelser i filmen för att informera senare händelser.
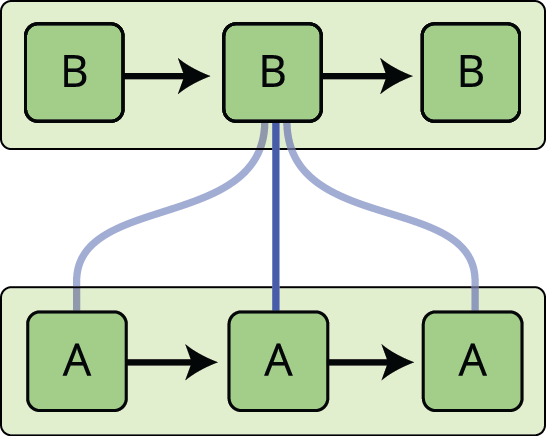
Rekursiva neurala nätverk löser detta problem. De är nätverk med slingor i dem, vilket gör det möjligt för information att bestå.

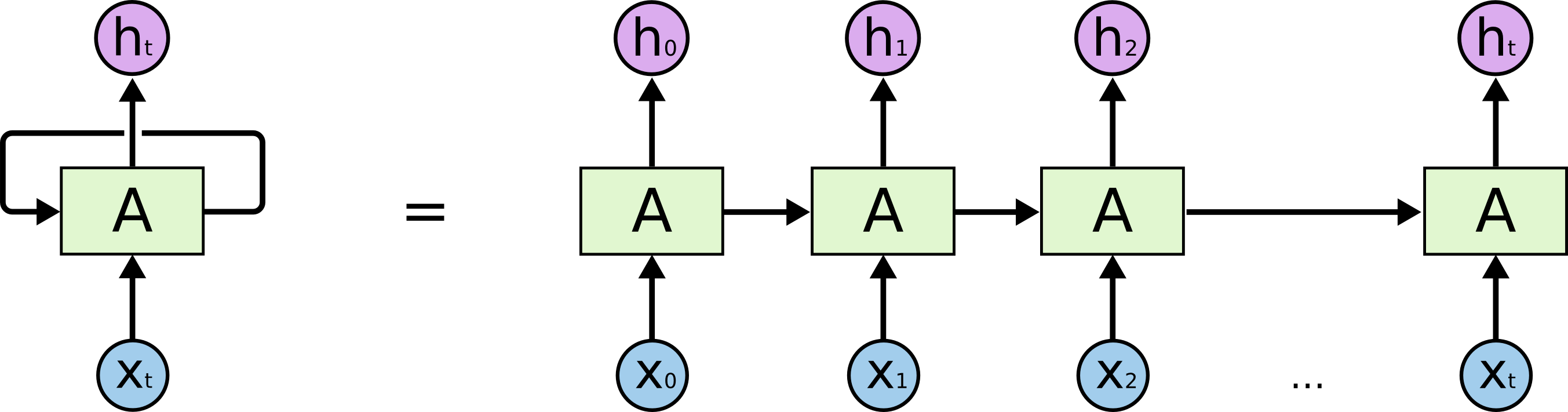
I diagrammet ovan tittar en del av det neurala nätverket, \(A\), på en viss inmatning \(x_t\) och ger ut ett värde \(h_t\). En slinga gör det möjligt att överföra information från ett steg i nätverket till nästa.
Dessa slingor gör att återkommande neurala nätverk verkar ganska mystiska. Om man tänker efter lite mer visar det sig dock att de inte skiljer sig så mycket från ett vanligt neuralt nätverk. Ett återkommande neuralt nätverk kan ses som flera kopior av samma nätverk som var och en skickar ett meddelande till en efterföljare. Tänk på vad som händer om vi rullar ut slingan:
Denna kedjeliknande karaktär avslöjar att återkommande neurala nätverk är intimt besläktade med sekvenser och listor. De är den naturliga arkitekturen för neurala nätverk att använda för sådana data.
Och de används verkligen! Under de senaste åren har man lyckats otroligt bra med att tillämpa RNN på en mängd olika problem: taligenkänning, språkmodellering, översättning, bildtextning… Listan kan göras lång. Jag överlåter diskussionen om de fantastiska prestationer man kan uppnå med RNN till Andrej Karpathys utmärkta blogginlägg The Unreasonable Effectiveness of Recurrent Neural Networks (Den orimliga effektiviteten hos återkommande neurala nätverk). Men de är verkligen ganska fantastiska.
En väsentlig del av dessa framgångar är användningen av ”LSTMs”, en mycket speciell typ av återkommande neurala nätverk som för många uppgifter fungerar mycket, mycket bättre än standardversionen. Nästan alla spännande resultat som bygger på återkommande neurala nätverk uppnås med dem. Det är dessa LSTMs som den här uppsatsen kommer att utforska.
Problemet med långsiktiga beroenden
En av de tilltalande egenskaperna hos RNNs är idén att de skulle kunna koppla tidigare information till den aktuella uppgiften, som till exempel att använda tidigare videobildar skulle kunna informera förståelsen av den aktuella bilden. Om RNNs kunde göra detta skulle de vara extremt användbara. Men kan de det? Det beror på.
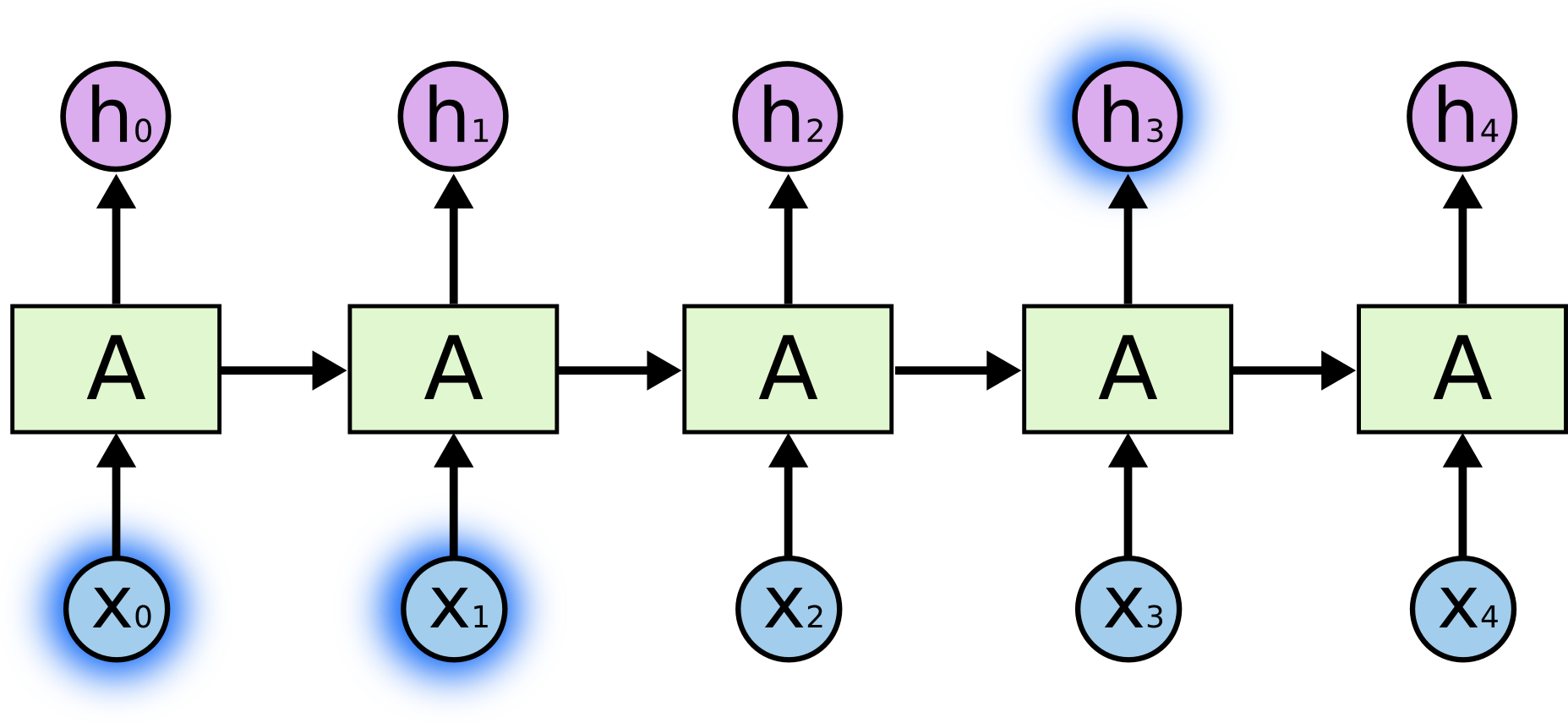
Under vissa omständigheter behöver vi bara titta på aktuell information för att utföra den aktuella uppgiften. Tänk till exempel på en språkmodell som försöker förutsäga nästa ord baserat på de föregående orden. Om vi försöker förutsäga det sista ordet i ”molnen är på himlen” behöver vi ingen ytterligare kontext – det är ganska uppenbart att nästa ord kommer att vara himmel. I sådana fall, där gapet mellan den relevanta informationen och det ställe där den behövs är litet, kan RNNs lära sig att använda den tidigare informationen.
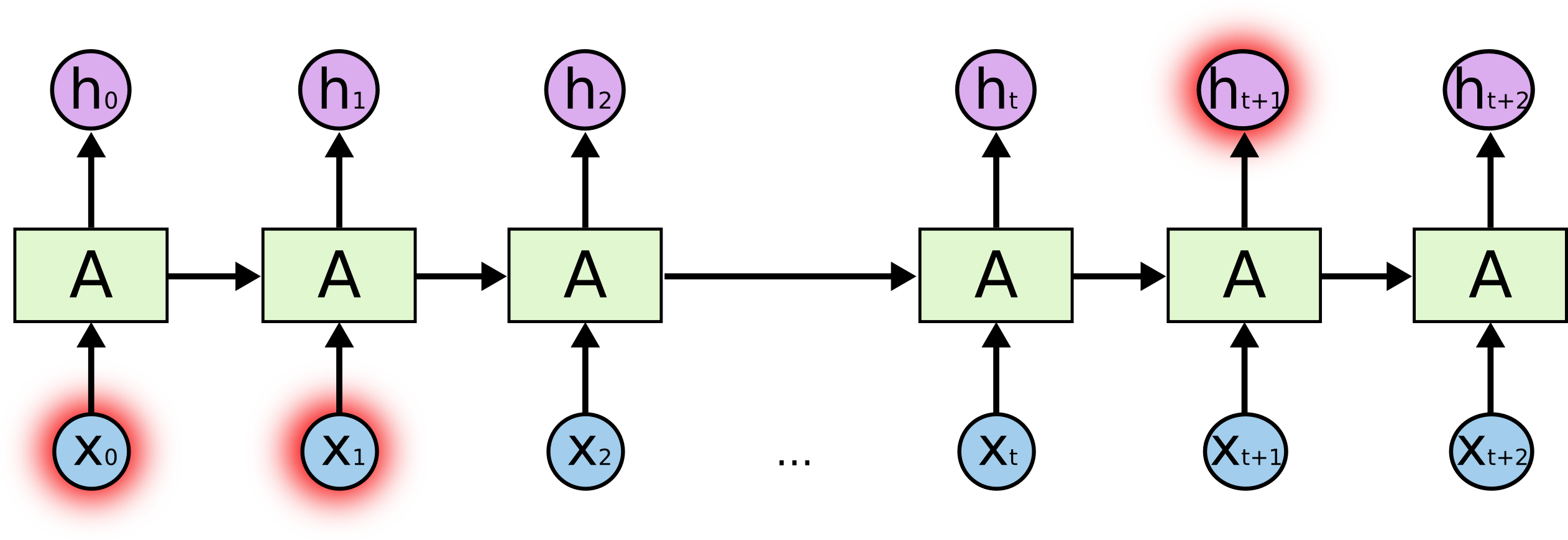
Men det finns också fall där vi behöver mer kontext. Tänk på att försöka förutsäga det sista ordet i texten ”Jag växte upp i Frankrike… Jag talar flytande franska”. Ny information tyder på att nästa ord troligen är namnet på ett språk, men om vi vill begränsa vilket språk det rör sig om behöver vi kontexten Frankrike, från längre tillbaka i tiden. Det är fullt möjligt att gapet mellan den relevanta informationen och den punkt där den behövs blir mycket stort.
Olyckligtvis blir RNNs oförmögna att lära sig att koppla ihop informationen när gapet växer.
I teorin är RNNs absolut kapabla att hantera sådana ”långtidsberoenden”. En människa skulle noggrant kunna välja parametrar för dem för att lösa leksaksproblem av denna form. Tyvärr verkar RNNs i praktiken inte kunna lära sig dem. Problemet undersöktes på djupet av Hochreiter (1991) och Bengio, et al. (1994), som fann några ganska grundläggande skäl till varför det kan vara svårt.
Tursamt nog har inte LSTM:s detta problem!
LSTM-nätverk
Nätverk för långvarigt korttidsminne – vanligen bara kallade ”LSTM:s” – är en speciell typ av RNN, som har förmågan att lära sig långsiktiga beroenden. De introducerades av Hochreiter & Schmidhuber (1997) och förfinades och populariserades av många personer i efterföljande arbeten.1 De fungerar oerhört bra på ett stort antal olika problem och används nu i stor utsträckning.
LSTMs är uttryckligen utformade för att undvika problemet med långsiktiga beroenden. Att komma ihåg information under långa perioder är praktiskt taget deras standardbeteende, inte något de kämpar för att lära sig!
Alla återkommande neurala nätverk har formen av en kedja av upprepande moduler av neurala nätverk. I standard-RNN kommer denna repeterande modul att ha en mycket enkel struktur, till exempel ett enda tanh-skikt.
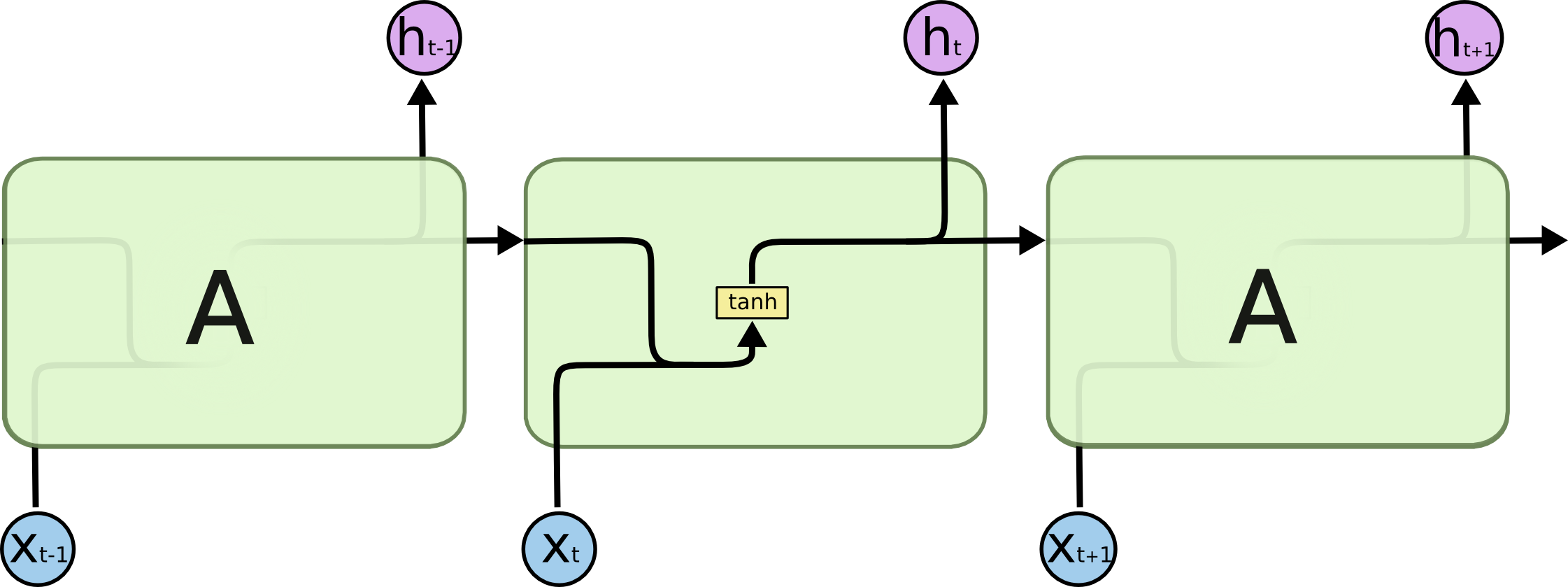
LSTMs har också denna kedjeliknande struktur, men den repeterande modulen har en annan struktur. Istället för att ha ett enda lager i det neurala nätverket finns det fyra, som interagerar på ett mycket speciellt sätt.

Oroa dig inte om detaljerna i vad som händer. Vi kommer att gå igenom LSTM-diagrammet steg för steg senare. För tillfället ska vi bara försöka bli bekväma med den notation vi kommer att använda.

I diagrammet ovan bär varje linje en hel vektor, från utgången från en nod till ingångarna från andra noder. De rosa cirklarna representerar punktvisa operationer, som vektoraddition, medan de gula rutorna är inlärda lager av neurala nätverk. Linjer som går samman innebär concatenation, medan en linje som delar sig innebär att dess innehåll kopieras och att kopiorna hamnar på olika ställen.
Kärnidén bakom LSTMs
Nyckeln till LSTMs är celltillståndet, den horisontella linjen som löper genom toppen av diagrammet.
Celltillståndet är ungefär som ett transportband. Det löper rakt ner i hela kedjan, med endast några mindre linjära interaktioner. Det är mycket lätt för information att bara flyta längs det oförändrat.
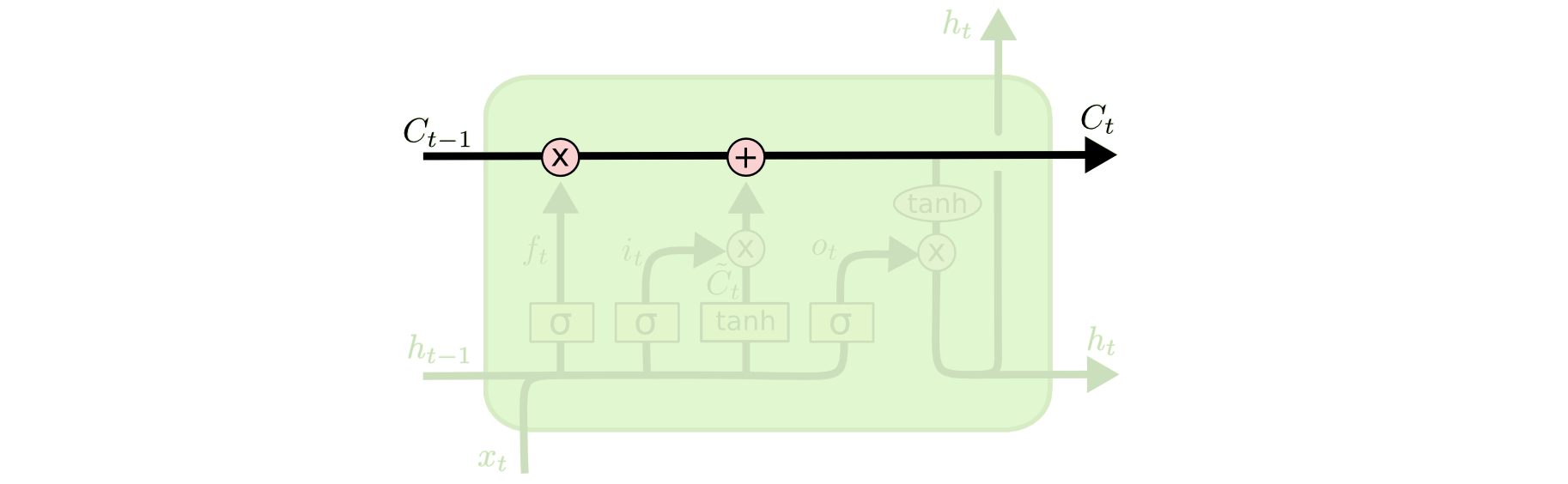
LSTM har förmågan att ta bort eller lägga till information till celltillståndet, noggrant reglerat av strukturer som kallas grindar.
G grindar är ett sätt att frivilligt släppa igenom information. De är sammansatta av ett sigmoidiskt neuralt nätskikt och en punktvis multiplikationsoperation.
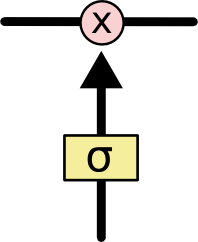
Det sigmoidiska skiktet ger ut tal mellan noll och ett, vilket beskriver hur mycket av varje komponent som ska släppas igenom. Ett värde på noll betyder ”släpp inget igenom”, medan ett värde på ett betyder ”släpp allt igenom!”
En LSTM har tre av dessa grindar, för att skydda och kontrollera celltillståndet.
Steg-för-steg LSTM Walk Through
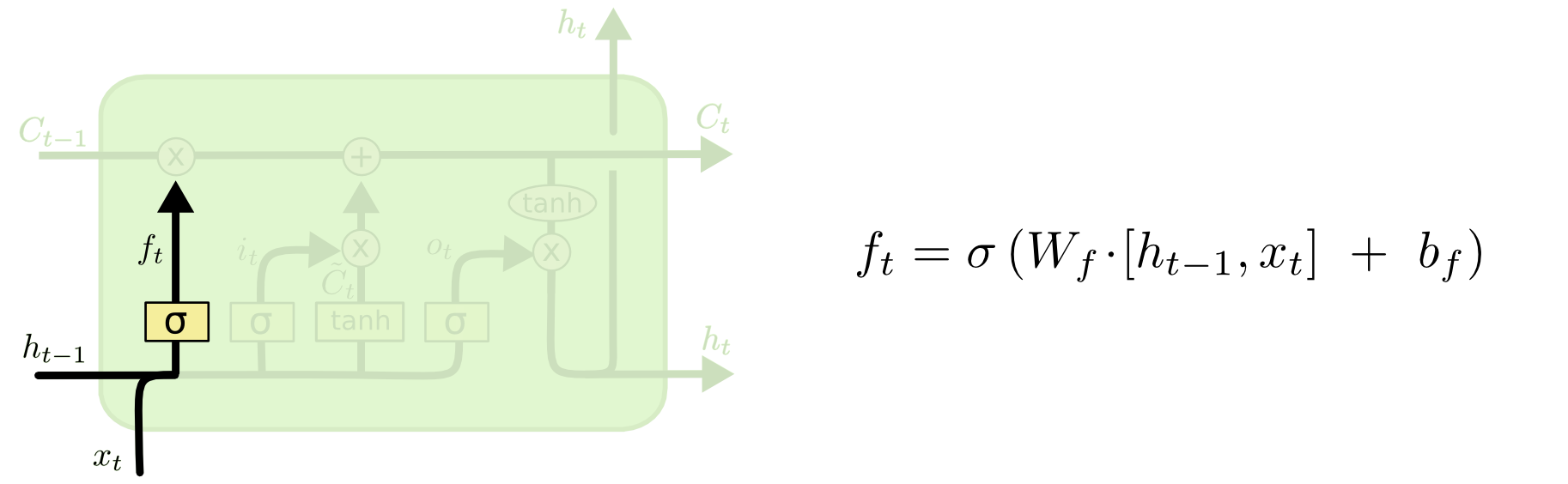
Det första steget i vår LSTM är att bestämma vilken information vi ska kasta bort från celltillståndet. Detta beslut fattas av ett sigmoidskikt som kallas ”forget gate layer”. Det tittar på \(h_{t-1}\) och \(x_t\) och matar ut ett tal mellan \(0\) och \(1\) för varje tal i celltillståndet \(C_{t-1}\). Ett \(1\) representerar ”behåll detta helt och hållet” medan ett \(0\) representerar ”gör dig av med detta helt och hållet.”
Vi återgår till vårt exempel med en språkmodell som försöker förutsäga nästa ord baserat på alla de föregående. I ett sådant problem kan celltillståndet innehålla det nuvarande subjektets kön, så att rätt pronomen kan användas. När vi ser ett nytt subjekt vill vi glömma det gamla subjektets kön.
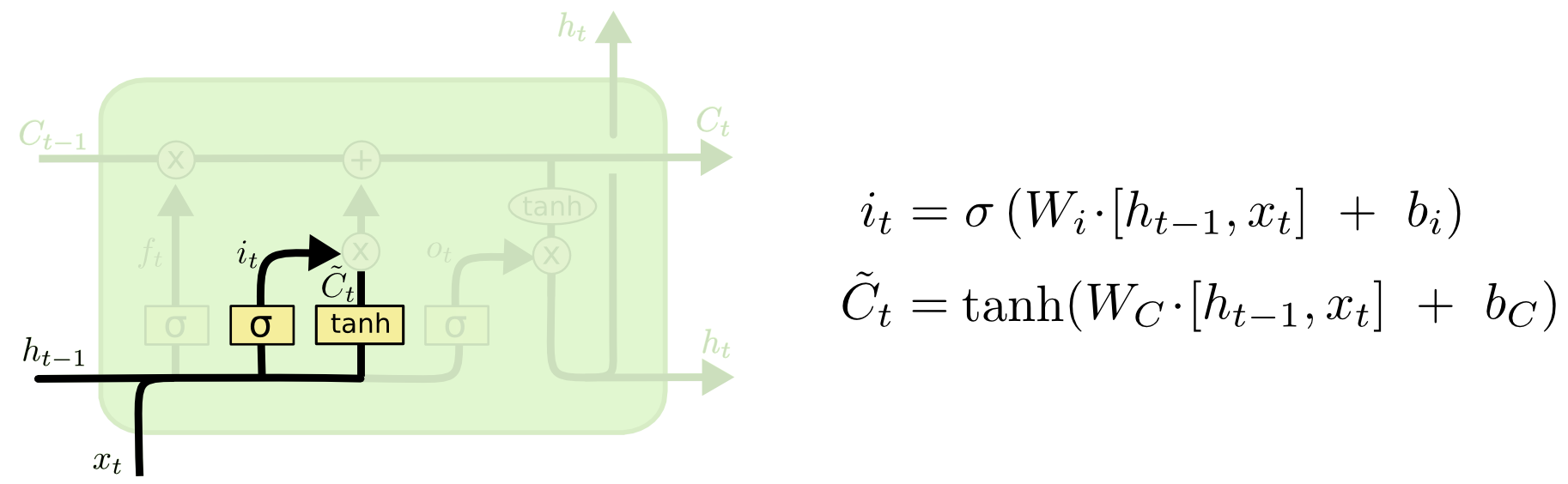
Nästa steg är att bestämma vilken ny information vi ska lagra i celltillståndet. Detta har två delar. Först bestämmer ett sigmoidskikt som kallas ”input gate layer” vilka värden vi ska uppdatera. Därefter skapar ett tanh-skikt en vektor av nya kandidatvärden, \(\tilde{C}_t\), som kan läggas till i tillståndet. I nästa steg kombinerar vi dessa två för att skapa en uppdatering av tillståndet.
I exemplet med vår språkmodell skulle vi vilja lägga till det nya subjektets kön till celltillståndet, för att ersätta det gamla som vi glömmer.
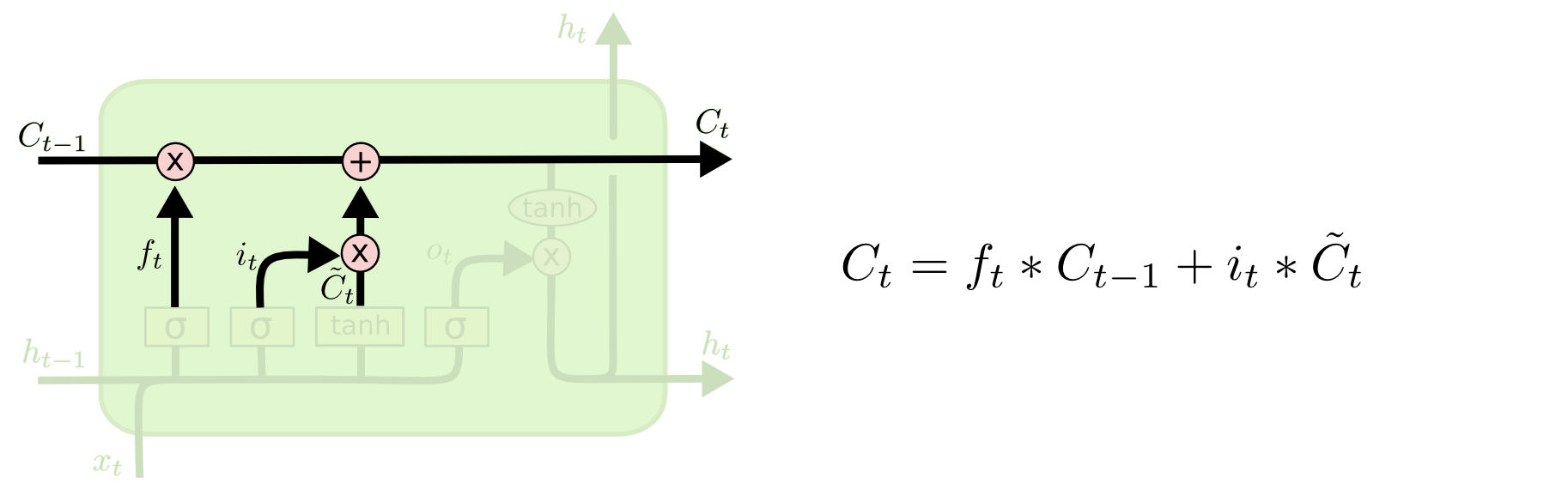
Det är nu dags att uppdatera det gamla celltillståndet, \(C_{t-1}\), till det nya celltillståndet \(C_t\). De tidigare stegen har redan bestämt vad vi ska göra, vi behöver bara faktiskt göra det.
Vi multiplicerar det gamla tillståndet med \(f_t\) och glömmer de saker som vi bestämde oss för att glömma tidigare. Sedan lägger vi till \(i_t*\tilde{C}_t\). Detta är de nya kandidatvärdena, skalade efter hur mycket vi beslutade att uppdatera varje tillståndsvärde.
I fallet med språkmodellen är det här vi faktiskt skulle släppa informationen om den gamla försökspersonens kön och lägga till den nya informationen, vilket vi beslutade i de tidigare stegen.
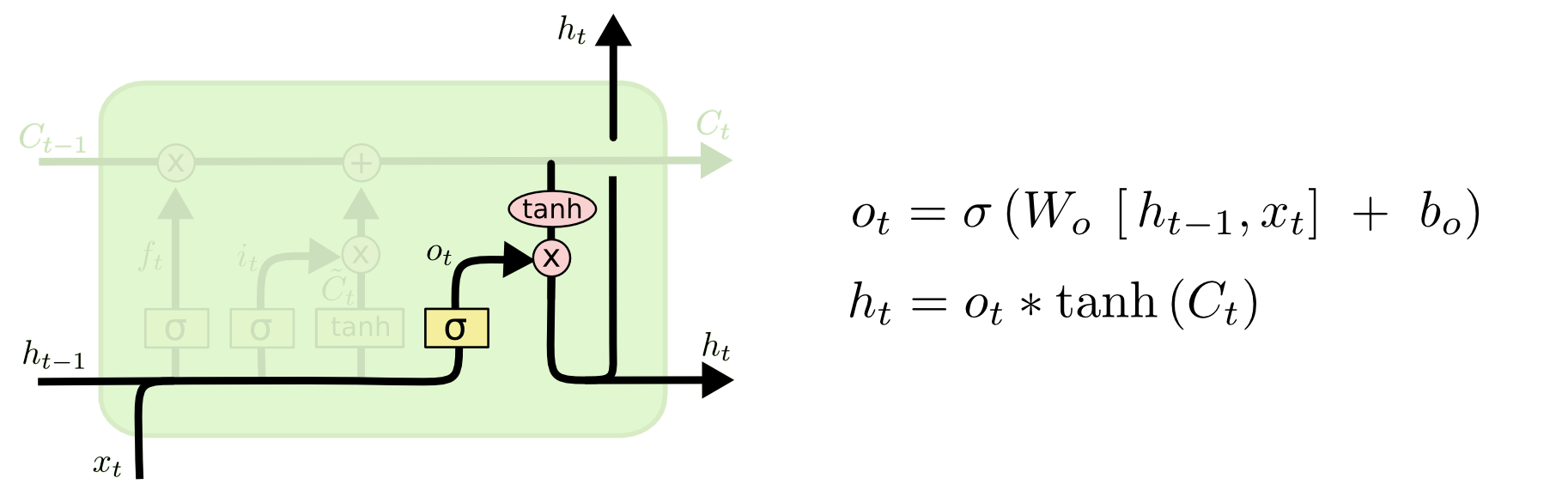
Slutligt måste vi bestämma vad vi ska ge ut. Denna utdata kommer att baseras på vårt celltillstånd, men kommer att vara en filtrerad version. Först kör vi ett sigmoidskikt som bestämmer vilka delar av celltillståndet vi ska ge ut. Sedan lägger vi celltillståndet genom \(\tanh\) (för att driva värdena så att de ligger mellan \(-1\) och \(1\)) och multiplicerar det med utdata från den sigmoida grinden, så att vi bara matar ut de delar som vi har bestämt att vi ska göra.
För språkmodellens exempel, eftersom den just såg ett subjekt, kanske den vill skicka ut information som är relevant för ett verb, i händelse av att det är vad som kommer härnäst. Den kan till exempel ge ut om subjektet är singular eller plural, så att vi vet vilken form ett verb ska böjas till om det är det som följer härnäst.
Varianter på Long Short Term Memory
Det jag har beskrivit hittills är en ganska normal LSTM. Men alla LSTM:er är inte likadana som ovanstående. Faktum är att det verkar som om nästan alla artiklar som handlar om LSTMs använder en något annorlunda version. Skillnaderna är små, men det är värt att nämna några av dem.
En populär LSTM-variant, som introducerades av Gers & Schmidhuber (2000), innebär att man lägger till ”peephole connections”. Detta innebär att vi låter grindlagren titta på celltillståndet.
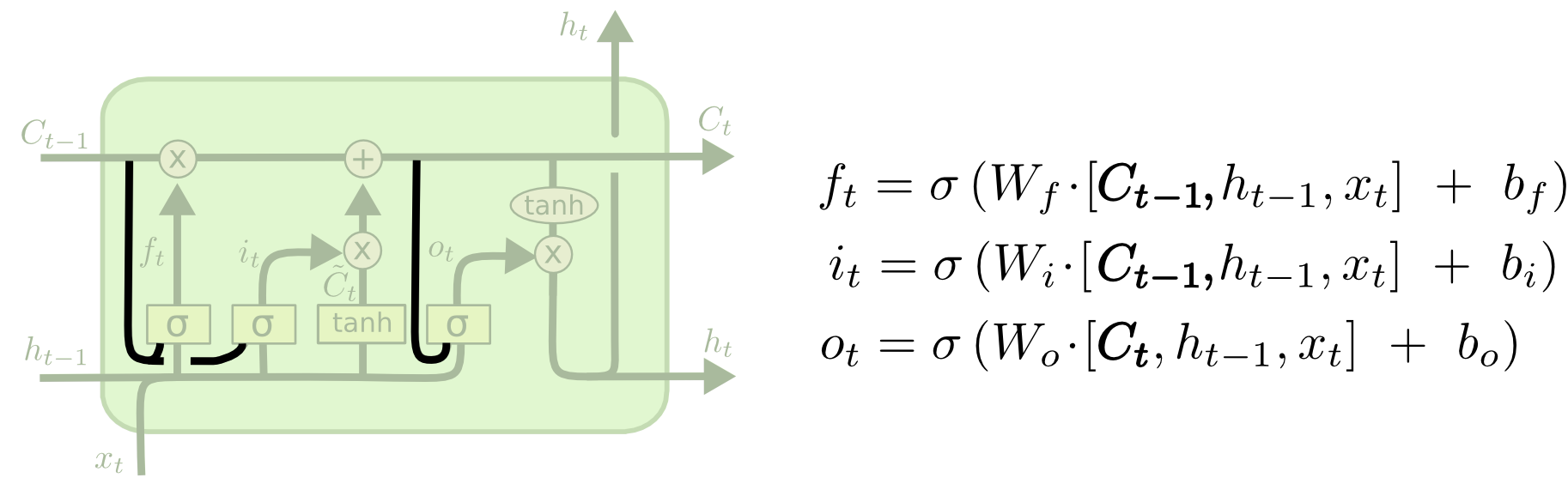
Det ovanstående diagrammet lägger till peepholes till alla grindar, men många artiklar kommer att ge vissa peepholes och inte andra.
En annan variant är att använda kopplade glöm- och ingångsgrindar. Istället för att separat bestämma vad som ska glömmas och vad vi ska lägga till ny information till, fattar vi dessa beslut tillsammans. Vi glömmer bara när vi ska mata in något i stället. Vi matar bara in nya värden till tillståndet när vi glömmer något äldre.
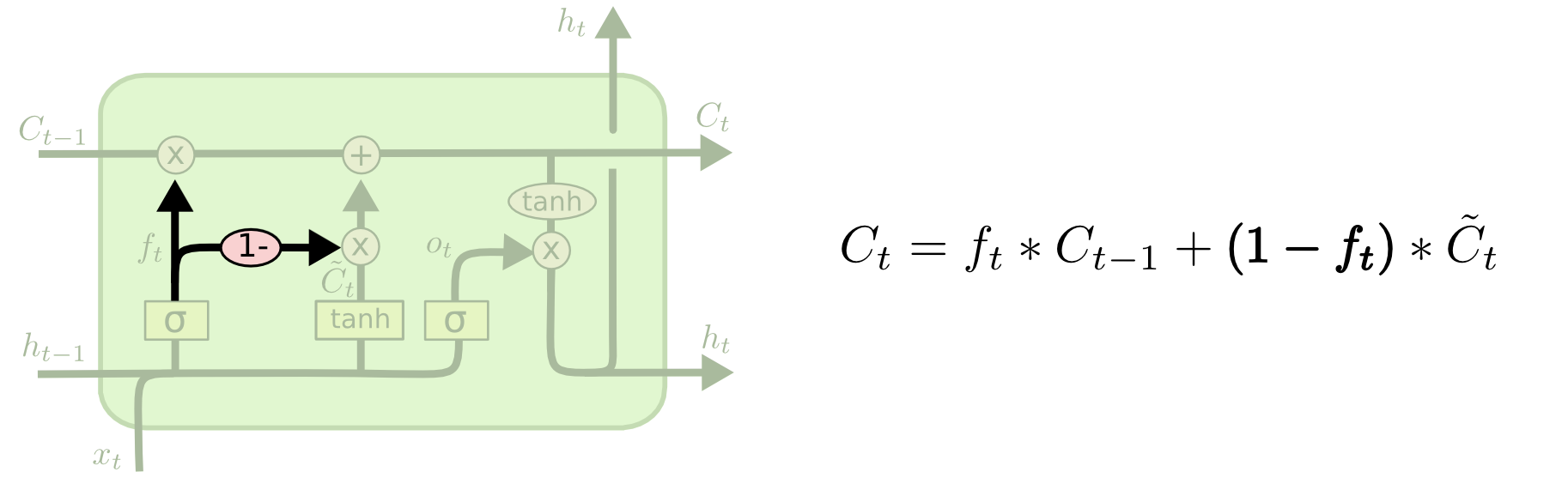
En något mer dramatisk variant av LSTM är Gated Recurrent Unit, eller GRU, som introducerades av Cho, et al. (2014). Den kombinerar forget- och ingångsgrindarna till en enda ”uppdateringsgrind”. Den slår också samman celltillståndet och det dolda tillståndet och gör några andra ändringar. Den resulterande modellen är enklare än vanliga LSTM-modeller och har blivit alltmer populär.

Detta är bara några av de mest anmärkningsvärda LSTM-varianterna. Det finns många andra, till exempel Depth Gated RNNs av Yao, et al. (2015). Det finns också några helt andra tillvägagångssätt för att hantera långsiktiga beroenden, som Clockwork RNNs av Koutnik, et al. (2014).
Vilken av dessa varianter är bäst? Spelar skillnaderna någon roll? Greff, et al. (2015) gör en fin jämförelse av populära varianter och konstaterar att de alla är ungefär lika bra. Jozefowicz, et al. (2015) testade mer än tiotusen RNN-arkitekturer och fann några som fungerade bättre än LSTMs på vissa uppgifter.
Slutsats
Tidigare nämnde jag de anmärkningsvärda resultat som människor uppnår med RNNs. I princip alla dessa resultat uppnås med hjälp av LSTMs. De fungerar verkligen mycket bättre för de flesta uppgifter!
Skrivet som en uppsättning ekvationer ser LSTMs ganska skrämmande ut. Förhoppningsvis har det att gå igenom dem steg för steg i den här uppsatsen gjort dem lite mer lättillgängliga.
LSTMs var ett stort steg i vad vi kan åstadkomma med RNNs. Det är naturligt att undra: finns det ytterligare ett stort steg? En vanlig åsikt bland forskare är: ”Det finns ett nästa steg och det är uppmärksamhet. Tanken är att låta varje steg i en RNN välja information att titta på från en större samling information. Om du till exempel använder en RNN för att skapa en bildtext som beskriver en bild, kan den välja en del av bilden att titta på för varje ord den matar ut. Xu, et al. (2015) gör faktiskt exakt detta – det kan vara en rolig utgångspunkt om du vill utforska uppmärksamhet! Det har kommit ett antal riktigt spännande resultat med hjälp av uppmärksamhet, och det verkar som om många fler ligger runt hörnet…
Attention är inte den enda spännande tråden inom RNN-forskningen. Grid LSTMs av Kalchbrenner, et al. (2015) verkar till exempel mycket lovande. Arbete där RNNs används i generativa modeller – som Gregor, et al. (2015), Chung, et al. (2015) eller Bayer & Osendorfer (2015) – verkar också mycket intressant. De senaste åren har varit en spännande tid för återkommande neurala nätverk, och de kommande lovar att bara bli ännu mer spännande!
Acknowledgments
Jag är tacksam mot ett antal personer som har hjälpt mig att bättre förstå LSTMs, kommenterat visualiseringarna och gett feedback på det här inlägget.
Jag är mycket tacksam mot mina kollegor på Google för deras användbara feedback, särskilt Oriol Vinyals, Greg Corrado, Jon Shlens, Luke Vilnis och Ilya Sutskever. Jag är också tacksam mot många andra vänner och kollegor som tagit sig tid att hjälpa mig, bland annat Dario Amodei och Jacob Steinhardt. Jag är särskilt tacksam mot Kyunghyun Cho för extremt tankeväckande korrespondens om mina diagram.
För det här inlägget övade jag mig i att förklara LSTMs under två seminarieserier som jag undervisade i neurala nätverk. Tack till alla som deltog i dessa för deras tålamod med mig och för deras feedback.
-
Förutom de ursprungliga författarna har många människor bidragit till den moderna LSTM. En icke uttömmande lista är: Felix Gers, Fred Cummins, Santiago Fernandez, Justin Bayer, Daan Wierstra, Julian Togelius, Faustino Gomez, Matteo Gagliolo och Alex Graves.
Mer inlägg
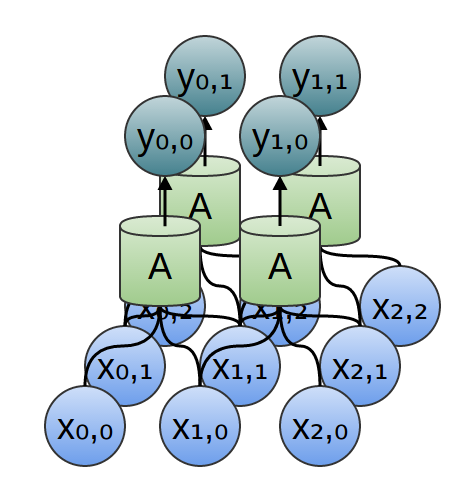
Attention and Augmented Recurrent Neural Networks
Om Distill
Conv Nets
Ett modulärt perspektiv
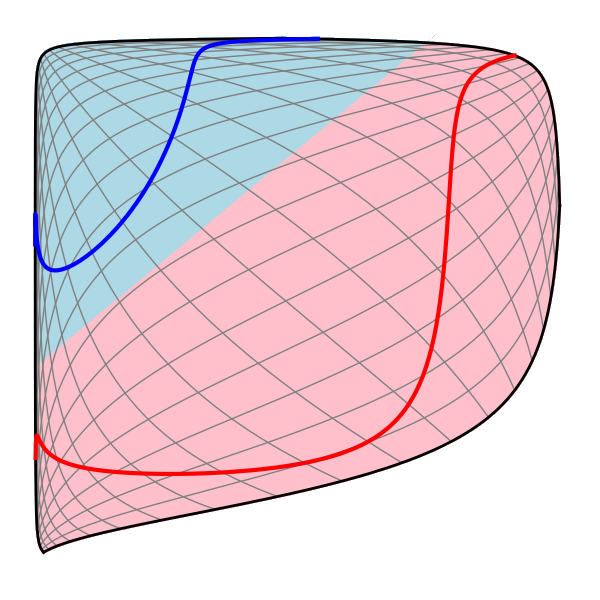
Neurala nätverk, Manifolds och topologi