Představujeme Kleinovu láhev

Pokud rádi pijete, pak Kleinova láhev není doporučená nádoba. Vypadá sice matně jako láhev, ale neuzavírá žádný objem, což znamená, že ve skutečnosti nemůže pojmout žádnou kapalinu. Cokoli nalijete „dovnitř“, se prostě zase vrátí ven.

Jak takovou podivnou věc zkonstruovat a proč byste ji chtěli zkonstruovat? Matematik Felix Klein, který láhev v roce 1882 objevil, ji popsal jako plochu, kterou „si lze představit tak, že obrátíme kus gumové trubičky a necháme ji projít skrz sebe tak, aby se vnější a vnitřní strana setkaly“.

Your browser does not support the video tag. přímý odkaz

Je zřejmé, že Kleinova láhev, stejně jako známější koule, je uzavřená plocha: je konečná v tom smyslu, že se vejde do konečné oblasti prostoru, ale mravenec by po ní mohl chodit donekonečna, aniž by narazil na hranici nebo přepadl přes okraj. Na rozdíl od koule, která má vnitřek i vnějšek, je Kleinova láhev jednostranná: při chůzi by náš mravenec mohl dosáhnout obou stran každého bodu povrchu. To je důvod, proč láhev neuzavírá žádný objem, a také odpověď na otázku „proč“: Kleinova láhev je zajímavá, protože v přírodě se nesetkáváme s mnoha jednostrannými útvary. (Další velmi pěkný obrázek Kleinovy láhve najdete zde.)

Möbiův pás je jednostranný – prohlédněte si jeho animovanou verzi. (Obrázek a animace Konrada Polthiera.)

Pokud je to trochu matoucí, vzpomeňte si na jednodušší příklad jednostranné plochy: slavný Möbiův pás. Můžete ho vyrobit tak, že vezmete dva konce proužku papíru, proužek zkroutíte a pak konce slepíte k sobě. Pokud použijete proužek papíru, jehož dvě strany mají různé barvy, například zelenou a oranžovou, snadno se přesvědčíte, že výsledný Möbiův proužek je jednostranný. Po stočení a slepení zjistíte, že z každého zeleného bodu se dostanete do každého oranžového bodu, aniž byste museli papír propichovat nebo lézt přes jeho okraj.

Na rozdíl od Kleinovy láhve má Möbiův proužek hranici – tvoří ji dva neslepené okraje původního proužku. Existuje však mezi nimi spojnice. Vezmeme-li dva Möbiovy proužky a vytvoříme uzavřený útvar spojením jejich hranic pomocí obyčejného oboustranného proužku, jak je ukázáno níže, dostaneme přesně Kleinovu láhev.

Your browser does not support the video tag.přímý odkaz

Tato skutečnost inspirovala matematika Lea Mosera ke složení limeriku:

Matematik jménem KleinMyslel si, že Möbiova páska je božská. řekl: „

Někteří matematici jsou opravdu všestranně nadaní!

Další zajímavou vlastností Kleinovy láhve je, že se protíná, což znamená, že ji lze těžko vyrobit z jediné gumové trubičky, jak navrhoval Klein. Přesně řečeno, výše zobrazený samokřižující se objekt není Kleinova láhev, ale (jak Klein naznačil) pouze její vizualizace. Abychom pochopili proč, představme si nejprve známější koblihu (matematicky známou jako torus). Torus můžete vytvořit ze čtvercového plátu gumy tak, že nejprve slepíte dvě protilehlé strany, čímž vznikne válec, a poté slepíte dvě hraniční složky tohoto válce, čímž získáte torus.

Vytvoření torusu:

Pokud se nechcete zabývat lepením, můžete si torus jednoduše představit jako čtverec, přičemž mějte na paměti, že protilehlé body na protilehlých stranách se považují za stejné. Když tedy posunete tvar nakreslený na „čtverci“ přes horní hranu, objeví se znovu na spodní hraně, a když ho posunete přes pravou hranu, objeví se znovu na levé hraně (a naopak).

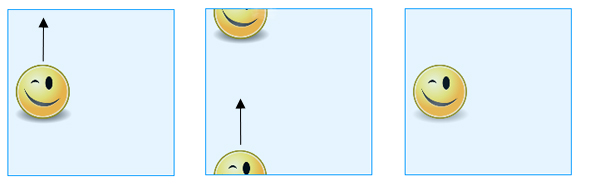
Když posunete tvar nakreslený na „čtverci“ přes horní hranu, objeví se znovu u spodní hrany.

Chcete-li získat pravou Kleinovu láhev, začněte stejným způsobem a určete protilehlé body na dvojici protilehlých stran čtverce. U druhé dvojice stran však neurčujte body, které jsou přímo protilehlé, ale body, které jsou šikmo protilehlé, jak je znázorněno na obrázku.

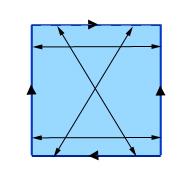
Sestavení Kleinovy láhve: Určete protilehlé body dvou protilehlých stran (na obrázku svislé) a poté určete šikmo protilehlé body na zbývajících dvou stranách. (Označíme-li body na horní a dolní straně zleva doprava čísly 0 až 1, pak bod s označením x na horní straně ztotožníme s bodem s označením 1-x na dolní straně)

Výsledný objekt je Kleinova láhev. Opět si ji můžete představit jako čtverec, přičemž mějte na paměti, které hraniční body jsou považovány za stejné. Pokud přesunete útvar přes jednu z hran, která měla identifikované protilehlé body (na našem obrázku svislé), objeví se znovu na opačné straně, jako předtím. Pokud jej však posunete přes jednu z hran, jejíž body byly identifikovány šikmo (na našem obrázku vodorovně), objeví se na opačné straně, ale posunutý a jako zrcadlový obraz svého původního já.

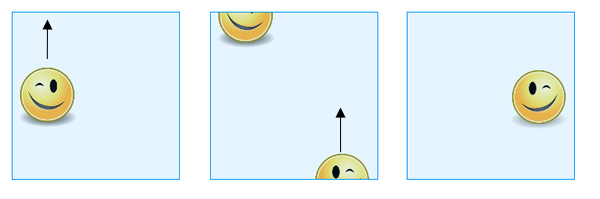
Přesuneme-li útvar přes horní hranu, objeví se přes spodní hranu, ale na druhé straně a jako zrcadlový obraz svého původního já.

Jediný způsob, jak tento útvar sestavit v trojrozměrném prostoru skutečným slepením bodů, je nechat ho protnout sám sebe. To se rovná určení dvojic bodů uvnitř původního čtverce, takže přísně vzato není výsledný tvar přesně stejný jako Kleinova láhev, která má určeny pouze hraniční body. Je to jen jeden ze způsobů, jak znázornit láhev v trojrozměrném prostoru (existují i jiné).

Zajímavé je, že pojmy „vnitřní“, „vnější“ a „jednostrannost“ závisí na okolním prostoru, v němž se objekt nachází. Například smyčka nakreslená na kusu papíru (ve dvourozměrném prostoru) má dobře definovaný vnitřek a vnějšek, ale smyčka nakreslená v trojrozměrném prostoru nikoli. Proto nemůžeme mluvit o jednostrannosti, pokud se nejprve nerozhodneme, jak plochu do trojrozměrného prostoru zasadit. Existuje však úzce související vlastnost, která je tvaru vlastní a nezávisí na okolním prostoru. Povrch se nazývá orientovatelný, pokud na něm nakreslený útvar nemůžete posunout dokola a zpět na místo, kde začal, takže vypadá jako jeho vlastní zrcadlový obraz. Jak můžete vidět v animaci připojené k obrázku vpravo, Möbiův pás není orientovatelný. A jak vidíte na obrázku se smajlíkem nahoře, není orientovatelná ani Kleinova láhev. abychom ji plně matematicky popsali, Kleinova láhev je uzavřená neorientovatelná plocha. Více se o ní dozvíte v článku Uvnitř Kleinovy láhve.

O autorovi

Marianne Freiberger je redaktorkou časopisu Plus.

.