Wat is de doorlaatbaarheid van het celmembraan?
Lezersmodus
Een van de kenmerkende eigenschappen van alle levende organismen is dat zij een kenmerkend mengsel van ionen en kleine moleculen bevatten. De samenstelling verschilt niet alleen van de omgeving, maar kan ook binnen de cel variëren. Zo kan de concentratie waterstofionen in sommige celcompartimenten 104 keer hoger zijn dan in andere (de mitochondriën bereiken een pH van wel 8; de lysosomen een pH van wel 4, BNID 107521, 106074). De verhouding tussen de concentraties van Ca2+-ionen in de extra- en intracellulaire vloeistofcompartimenten kan opnieuw 104-voudig zijn (BNID 104083). Dit concentratieverschil is zo groot dat voor het transport van een Ca2+ ion over het membraan, van het intra- naar het extracellulaire compartiment, de energie nodig is van meer dan één proton of natrium ion dat langs de proton-motorkracht gradiënt naar beneden stroomt. Om dit in te zien moet de lezer zich de vuistregel uit onze trucjeslijst herinneren dat voor het tot stand brengen van een orde van grootte potentiaalverschil 6 kJ/mol (≈2 kBT) nodig is. Deze energie kan bijvoorbeeld worden bereikt door het transport van één elektrische lading door een potentiaalverschil van 60 mV. Om een concentratieverhouding van vier orden van grootte te bereiken zou dan een lading moeten reizen door een elektronendrijfkracht van ongeveer 240 mV (eigenlijk nog meer door de dubbele lading van het calciumion). Dit ligt zeer dicht bij de doorslagspanning van het membraan zoals besproken in het vignet over “Wat is het elektrisch potentiaalverschil over membranen?”. Inderdaad wordt de hoge concentratieverhouding van Ca2+ gewoonlijk bereikt door koppeling aan het transport van drie natriumionen of de hydrolyse van ATP, die helpt het vereiste dichtheidsverschil te bereiken zonder het membraan gevaarlijk te bekrachtigen.
De tweede wet van de thermodynamica leert ons dat, in het algemeen, de aanwezigheid van concentratiegradiënten uiteindelijk zal worden afgeblazen door massatransportprocessen, die systemen gestaag naar een toestand van evenwicht drijven. Maar hoewel de tweede wet van de thermodynamica ons vertelt wat de aard is van de uiteindelijke toestand van een systeem (b.v. uniforme concentraties), vertelt zij ons niet hoe lang het zal duren om die toestand te bereiken. Membranen zijn geëvolueerd om een zeer effectieve barrière te vormen voor de spontane overdracht van vele ionische en moleculaire soorten. Om de tijdschaal voor het egaliseren van concentraties te schatten, moeten we de snelheid van massatransport kennen, die afhangt van belangrijke materiaaleigenschappen zoals diffusieconstanten en permeabiliteiten.
Een zeer succesvolle klasse van “wetten”, die het gedrag beschrijven van systemen die een kleine afwijking van het evenwicht hebben ondergaan, zijn de lineaire transportwetten. Deze wetten stellen een eenvoudig lineair verband tussen de transportsnelheid van een bepaalde grootheid en de bijbehorende drijvende kracht. Voor massatransport is er een lineair verband tussen de flux (d.w.z. het aantal moleculen dat per oppervlakte-eenheid per tijdseenheid passeert) en het concentratieverschil (dat dient als de relevante drijvende kracht). Voor het transport over membranen zijn deze ideeën gecodificeerd in de eenvoudige vergelijking (voor neutrale opgeloste stoffen) j= – p-(cin-cout), waarbij j de netto flux in de cel is, cin en cout de concentraties aan de binnen- en buitenzijde van het membraangebonden gebied, en p een materiaalparameter is die bekend staat als de permeabiliteit. De eenheden van p kunnen worden afgeleid door op te merken dat de flux eenheden heeft van aantal/(oppervlakte x tijd) en de concentratie eenheden heeft van aantal/volume, wat impliceert dat de eenheden van p zelf lengte/tijd zijn. Zoals vele transportgrootheden (b.v. elektrische geleidbaarheid van materialen die meer dan 30 orden van grootte omvatten), heeft de permeabiliteit een zeer groot dynamisch bereik zoals geïllustreerd in figuur 1. Zoals in de figuur te zien is, hebben lipide bilayers een bijna 1010-voudig bereik van permeabiliteit.
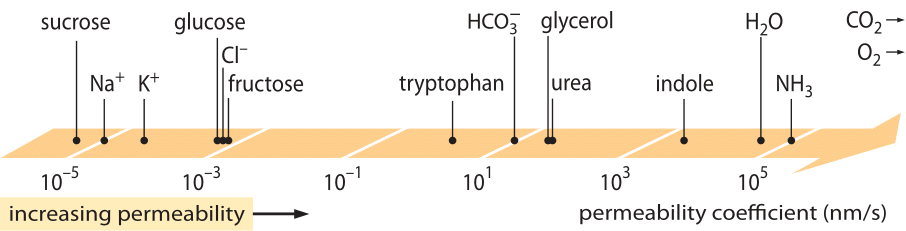
Figuur 1: Het grote bereik van membraanpermeabiliteit van verschillende verbindingen in de cel. De membranen zijn het meest doorlaatbaar voor niet-geladen verbindingen en het minst voor geladen ionen. Merk op dat door het bestaan van ionenkanalen de schijnbare permeabiliteit wanneer zij open zijn verscheidene orden van grootte hoger zal zijn. De eenheden zijn gekozen als nm/s en enkele nm is de karakteristieke membraanbreedte. Figuur aangepast uit R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. De waarde voor glucose is kleiner dan in Robertson, gebaseerd op verschillende bronnen zoals BNID 110830, 110807. Andere bronnen van gegevens: BNID 110729, 110731, 110816, 110824, 110806.
Welke fysisch-chemische parameters bepalen de plaats van een verbinding op deze schaal van permeabiliteiten? Een vuistregel is dat kleine moleculen een hogere permeabiliteit hebben dan grotere moleculen. Een andere vuistregel is dat neutrale verbindingen vele orden van grootte sneller het membraan kunnen passeren dan vergelijkbare geladen verbindingen. Onder de geladen verbindingen hebben negatieve (anionische) verbindingen een veel hogere permeabiliteit dan positieve (kationische) verbindingen. De zogenaamde Overton-regel stelt dat de membraanpermeabiliteit toeneemt met de hydrofobiciteit, waarbij hydrofobiciteit de neiging is van een verbinding om een apolair oplosmiddel te verkiezen boven een polair (waterig) oplosmiddel. De Overton-regel voorspelt dat geladen moleculen (niet-hydrofoob), zoals ionen, een lage permeabiliteit zullen hebben omdat zij een energetisch nadeel ondervinden bij het doordringen van het membraan, terwijl opgeloste gassen zoals O2 en CO2, die hydrofoob zijn (omdat zij ongeladen en symmetrisch zijn), een hoge permeabiliteit zullen hebben. De doorlaatbaarheid van lipide bilaagmembranen voor CO2 geeft inderdaad waarden die 0,01-1 cm/s zijn (ja, doorlaatbaarheidsmetingen hebben zeer grote onzekerheden tussen verschillende laboratoria, BNID 110004, 110617, 102624), hoger dan alle andere in figuur 1 getoonde waarden. Deze waarde toont aan dat de barrière die door het celmembraan wordt opgeworpen, in feite een minder grote belemmering vormt dan de barrière die wordt veroorzaakt door de niet-geroerde laag water die het celmembraan van buitenaf opslokt. Een dergelijke gevolgtrekking kan worden afgeleid uit de vergelijking voor de permeabiliteitscoëfficiënt van een obstakel, gegeven door p=K x D/l waarbij l de breedte is, D de diffusiecoëfficiënt en K de verdelingscoëfficiënt tussen het medium en het materiaal van het obstakel. Dit wordt ook wel het “oplosbaarheid-diffusie”-model voor permeabiliteit genoemd, waarbij de K- en de D-effecten twee stappen zijn die de permeabiliteit beïnvloeden. Voor een niet-bevloeide laag water is K=1 aangezien deze zeer vergelijkbaar is met de media, maar voor membranen is de waarde voor alle behalve het meest hydrofobe materiaal gewoonlijk verscheidene orden van grootte kleiner dan 1. Deze afhankelijkheid van K is de kern van de bovengenoemde Overton-regel. De hoge permeabiliteit voor CO2 suggereert ook dat kanalen zoals aquaporines, waarvan werd gesuggereerd dat ze zouden dienen voor gastransport in de cel, niet nodig zijn omdat het membraan doorlatend genoeg is. Om te zien hoe de membraaneigenschappen de chemische samenstelling van metabolieten beïnvloeden, berekenen we de tijd van lekkage voor verschillende verbindingen
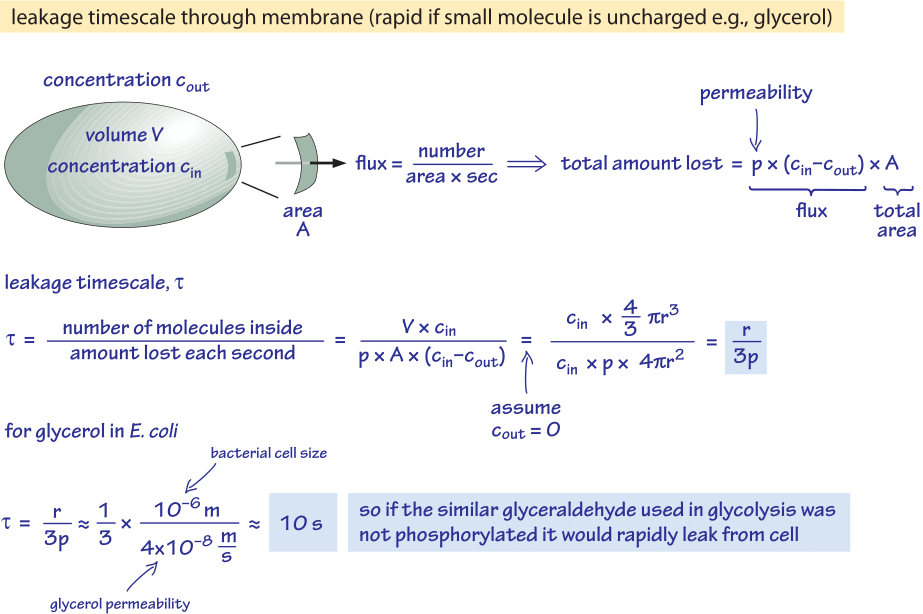
Figuur 2: Berekening van de tijdschaal waarop niet-gefosforyleerde glucosemoleculen passief uit een bacteriële cel diffunderen. De functionele implicaties worden vervolgens bekeken voor snelgroeiende cellen, waar het effect verwaarloosbaar is, en voor cellen in stationaire toestand, waar het een aanzienlijk weglekken van hulpbronnen kan veroorzaken.
Wij beschouwen bijvoorbeeld glycerol. De analyse in figuur 2 geeft een schatting van het tijdstip waarop het uit de cel lekt, indien het molecuul niet wordt gefosforyleerd of anderszins in een meer hydrofiele vorm wordt omgezet. De permeabiliteit van het celmembraan voor glycerol is p≈10-100 nm/s (BNID 110824), zoals kan worden afgelezen uit figuur 1. De tijdschaal voor een glycerolmolecuul in de cel om terug te ontsnappen naar het omringende medium, ervan uitgaande dat er geen terugstroom in de cel is (cout=0), kan ruwweg worden geschat door op te merken dat de uitstroom uit de cel p-A-cin is, waarbij A het celoppervlak is. De tijdschaal wordt gevonden door de totale hoeveelheid in de cel, V-cin (waarbij V het celvolume of nauwkeuriger het celwatervolume is), te nemen en te delen door deze flux, hetgeen voor een bacteriecel (r≈1 μm) resulteert in een tijdschaal:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Dit is een ruwe schatting omdat we geen rekening hebben gehouden met de afnemende concentratie van cin met de tijd, die een correctiefactor van 1/ln(2) zal opleveren, d.w.z. minder dan een 2-voudige toename. Wat wij uit deze ramingen leren is dat indien de glycolytische tussenproducten glyceraldehyde of dihydroxyaceton, die sterk op glycerol lijken, niet gefosforyleerd zouden worden, waardoor een lading zou worden toegevoegd, zij door diffusie door het celmembraan aan het medium zouden worden afgestaan. In laboratoriummedia, waar een koolstofbron in overvloed wordt aangevoerd, is dit geen groot probleem, maar in een natuurlijke omgeving waar de cellen in de stationaire fase vaak wachten op een gelukkige puls van voedingsstoffen (E. coli wordt verondersteld maandenlang niet te groeien nadat het uit het lichaam is verwijderd voordat het een nieuwe gastheer vindt), kan de cel zijn verliezen beperken door ervoor te zorgen dat metabolische tussenproducten een lading krijgen die voorkomt dat ze opnieuw de barrière van de lipide-bilaag passeren.




