Note: dit is pagina één van onze Vortex Math analyse. Klik hier als u op zoek bent naar de interactieve Vortex-N-k app.
Die Professor Puzzler,
Ik heb mensen horen praten over “Vortex Math,” en ik wil begrijpen wat het is. Kunt u me helpen?
Mystified in Maine
Dear Mystified,
Ik zou u graag willen helpen. Dit wordt soms een beetje technisch, maar om het interessant te maken, heeft mijn goede vriend Marko-11 van Wunfishia aangeboden om een gastbericht te doen. Marko-11 is een beetje vreemd (letterlijk) – hij heeft elf vingers in plaats van tien, en dat geeft hem een heel nieuw perspectief op wiskunde. Als je hem tot het einde van zijn uitleg volgt, garandeer ik je dat je van de rit zult genieten! Marko?
Dank u, professor Puzzler. Ik moet uw lezers waarschuwen dat ik hier wat lichte getaltheorie ga behandelen, maar als wiskunde niet hun sterkste kant is, kunnen ze hun ogen laten verslappen tijdens het wiskundegedoe, en gewoon naar mijn commentaar op de mooie plaatjes kijken.
Ik wil graag beginnen met ervoor te zorgen dat al uw vrienden begrijpen dat niet iedereen telt zoals zij doen. De meeste van je vrienden tellen waarschijnlijk in een getallenstelsel genaamd basis tien, dat de volgende cijfers heeft: 0, 1, 2, 3, 4, 5, 6, 7, 8, en 9. Niet ongebruikelijk, want ze hebben allemaal tien vingers. Ik, aan de andere kant (bij wijze van spreken), reken in de basis elf (je kunt waarschijnlijk wel raden waarom). Mijn telsysteem heeft een extra cijfer, net zoals ik een extra cijfer heb. Mijn cijfers zijn 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, en A. “A?” Je zou kunnen zeggen, “Dat is een letter, geen cijfer!” Waar, waar, maar telkens wanneer je in een basis groter dan tien werkt, heb je extra cijfers nodig, en in plaats van nieuwe symbolen uit te vinden, pakken we gewoon symbolen die nergens anders voor worden gebruikt (met excuses aan mijn vrienden de leraren Engels!)
Nu, omdat ik reken in basis elf, schrijf ik getallen heel anders. Bijvoorbeeld, als ik het getal 34 wil schrijven, schrijf ik “31.” Waarom? Omdat het betekent “3 elevens, plus 1 meer.” Het getal 87, schrijf ik “7A,” omdat 7 elevens plus A (dat is uw getal 10) is 87.
Dus ik ga wat fancy rekenwerk doen, en het gaat allemaal in basis elf, dus je zult goed moeten opletten om me te volgen.

Eerst, ga ik een cirkel tekenen, en markeer al mijn cijfers rond de omtrek. Wel, eigenlijk, niet allemaal; ik sla nul over. Vraag me niet waarom; ik weet niet zeker of ik daar een goede reden voor heb, maar het zorgt ervoor dat alles goed komt. Dus vertrouw me maar. Ik heb elf vingers, dus hoe kan ik het mis hebben?
Oké, nu ik mijn cirkel getekend heb, ga ik de getallen verbinden, in het volgende patroon. Ik begin met 2 en verdubbel het. Het resultaat is 4. Dus verbind ik 2 en 4. Nu verdubbel ik 4. Dat is 8, dus verbind ik 4 en 8. Nu verdubbel ik 8, en dat is … uh oh … dat is 15. (Ik weet wat je denkt – het is 16. Maar dat is in basis tien. In basis elf wordt 16 geschreven als 15, want 1 elf plus 5 meer is 16).
Mooi, maar ik heb geen cijfer 15. Dat is niet erg…ik tel gewoon de 1 en de 5 op tot 6, en dan verbind ik de 8 en de 6. Nu verdubbel ik 15 (basis elf) en krijg ik 2A (dat is 32 voor jou!). Nu tel ik de cijfers 2 + A = 11 (basis elf) bij elkaar op. Omdat ik geen cijfer 11 heb, tel ik de cijfers bij elkaar op: 1 + 1 = 2, en dus trek ik een lijn tussen 6 en 2.

Wauw! Dat ziet er echt cool uit! Het is net een mooi oneindigheidssymbool, dat is de manier van het universum om me te vertellen dat ik met iets speciaals bezig ben dat zal resulteren in oneindige alles voor iedereen!
Om het nog interessanter te maken, als ik 2A verdubbel, en mijn kaartproces doe, komt het uit op 4, en de volgende verdubbeling komt uit op 8, dan 6, en het herhaalt zich steeds weer, wat natuurlijk een symbool is van de oneindige rijkdom die me te wachten staat als ik dit idee eenmaal aan andere Wunfishians heb verkocht!
Maar hoe zit het met arme kleine 3, 5, 7, 9, en A? Wat zijn hun kaarten? Hier wordt het ECHT cool: 1 hoort bij 2, 3 bij 6, 5 bij A, 7 bij 4, en 9 bij 8. Met andere woorden, behalve 5, gaan ze allemaal rechtstreeks naar de oneindigheidscyclus, waardoor ik nog meer oneindige energie, rijkdom en kankerbestrijdingspotentieel krijg dat ik al ontdekt heb. Wat? Heb ik je niet verteld over het bestrijden van kanker? Oh jawel. Dat is een gegeven.
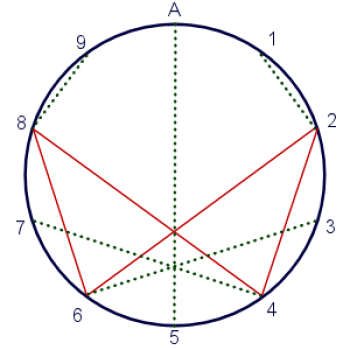
En waar komt A overeen mee? Dat is het verbazingwekkende ding; A maps to ITSELF. Het maakt niet uit hoe vaak je het verdubbelt, A blijft gewoon naar zichzelf wijzen. Dat zegt me dat A (jouw getal 10) de magische constante is die het universum regeert en de goddelijke taal van de wiskunde samenbindt.
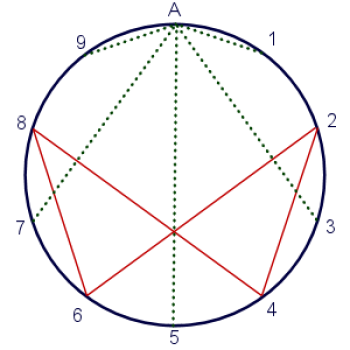
Dit hele ding zou er eigenlijk veel cooler uitzien als ik, in plaats van 1, 3, 7 en 9 in de oneindige lus te stoppen, ze in mijn magische getal zou stoppen. Vraag me niet waarom, ik heb geen reden nodig. Het ziet er gewoon cool uit, dus ik ga het doen.
Nu ziet mijn vortex-diagram eruit als oneindigheid onder een kerstboom, wat de manier van het universum is om me te vertellen dat dit zijn geschenk aan mij is.
Niet helemaal. Zie je, ik heb Vortex Wiskunde niet uitgevonden. Het is uitgevonden door een arme kerel (ik noem hem graag Marko-10) die, helaas, maar 10 vingers had. En omdat hij maar 10 vingers had, maakte hij de trieste fout om dit alles in basis tien te doen.
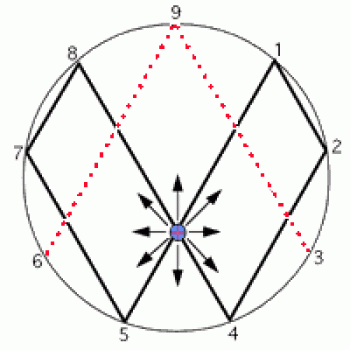
Natuurlijk was zijn vortex diagram niet zo mooi als het mijne. Merk op dat zijn oneindigheidssymbool veel minder elegant is dan het mijne, en wat extra verdubbeling vereist om terug te keren naar de oneindige goedheid. Merk ook op dat hij niet echt wist wat te doen met die arme kleine 3 en 6, die snobistisch alleen maar heen en weer naar elkaar verwijzen, en niet terugvloeien in zijn oneindige energievoorziening.
En heeft zijn kerstboom wel een stam? Nee, die heeft hij niet. En er is maar één set takken, dus er passen niet veel cadeautjes onder die boom.
Wat is dat voor een rare pijl in het midden? Blijkbaar maakt dat het hele ding het symbool van verlichting. Nou, zo verlicht als je kunt zijn als je een tienvingerig wezen bent! Als je verlicht genoeg bent, zal dit symbool je helpen de geheime naam van God te ontdekken – althans, dat is wat Marko-10 zegt. Maar ik vermoed dat dat afhangt van het feit of God ook slechts tien vingers heeft. (Voor het geval je het nog niet door had, Marko-10 doet niet aan wiskunde; hij doet aan Bahá’í mystiek.)
Oh, ja, en omdat Marko tien vingers heeft, denkt hij dat NEGEN het magische getal is dat de samenbindende bla-bla-bla van het universum samenbindt, en kanker zal genezen, ons van gratis energie zal voorzien, en misschien ook kaalheid zal genezen. Waarom? Omdat het universum er blijkbaar om geeft dat hij maar tien vingers heeft in plaats van elf.
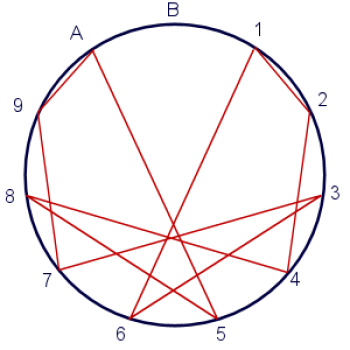
Dank je voor deze uitleg, Marko-11. Ik hoop dat je een goede reis terug naar Wunfishia hebt (ik weet het, het is een lange reis van hier naar daar, en er zijn overal grappige dingen!). Oh, en bedankt dat je me hebt voorgesteld aan je neef uit Blufishia, Marko-12 (ik weet zeker dat iedereen kan bedenken waarom hij Marko-12 heet). Marko-12 deed zijn eigen magische analyse van getallen in basis twaalf. Hij kwam met een heel cool vortex diagram dat een combinatie is van een adelaar en een pentagram.
Toeval? Ik ben er zeker van van niet. Ik weet zeker dat het de manier van het universum is om hem te vertellen dat hij tot grote hoogten zal stijgen als hij maar naar de sterren reikt.
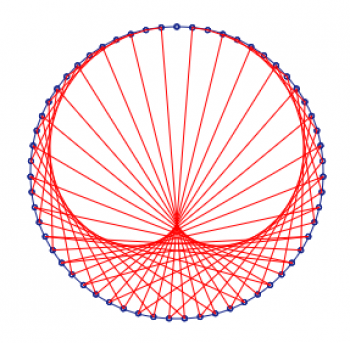
Natuurlijk, zelfs Marko-12 kan geen kaarsje branden voor de genialiteit van de oude Babyloniërs; als de vortex-gebaseerde “wiskundigen” van vandaag maar zo geavanceerd waren als die jongens, dan zou hun vortex-diagram eruit hebben gezien als dit verbazingwekkende kunstwerkje! En ja, dat is echt één enkele lus die elk cijfer in de cirkel raakt behalve hun basis zestig cijfer voor 59. Met alle respect voor Marko-10, FIFTY-NINE is WAY cooler dan NINE!
Een laatste opmerking: De VBM mensen (Vortex Based Math) geloven dat hun magische diagram een “goddelijke code” is, maar of je Galileo’s uitspraak “Wiskunde is de taal waarmee God het universum heeft geschreven” nu wel of niet gelooft, het valt niet te ontkennen dat het grondtal een volledig menselijke constructie is. Dus als hun diagram “goddelijk” is, dan zijn dat ook alle ontelbare (letterlijk oneindig!) prachtige diagrammen (en bijbehorende prachtige patronen!) die ze negeren omdat ze gebonden zijn aan, en vastlopen in, het getal tien.
Het kostte me in totaal 5 minuten om een rigoureus wiskundig bewijs te ontwikkelen dat als je in de basis N werkt, N-1 hun “magische getal” gedrag heeft. Als het echte wiskundigen waren, zou dat het soort werk zijn dat ze zouden doen, maar het zijn Baha’i mystici in plaats van wiskundigen, en ze zien door de bomen het bos niet meer vanwege hun eigen trieste kerstboompje…
In plaats van je tijd met hen te verdoen, kun je beter wat echt plezier hebben – leer werken in andere grondslagen dan de basis tien, en maak dan je eigen vortex-diagrammen. Zullen ze je helpen vrije energie te creëren? Of acne genezen? Natuurlijk niet, maar ze zijn zeker mooi, en ze functioneren ook als echt leuke Rorchach Tests die je meer over jezelf vertellen dan over de aard van het universum.
Professor Puzzler
P.S. Hier is een visueel hulpmiddel om je te helpen een voorproefje te krijgen van “vortex diagrammen” in andere grondslagen: Beyond Vortex Based Math