Puntsymmetrie bestaat wanneer de figuur om één punt is getekend.

Dit punt wordt het middelpunt van de figuur of het middelpunt van de symmetrie genoemd. In de figuur hiernaast zien we dat er voor het punt X op de figuur een punt X’ aan de andere kant van het middelpunt bestaat, dat recht tegenover X ligt en op de figuur. We zeggen dat de figuur symmetrisch is om het middelpunt.
Note:
Wanneer we een figuur 180° draaien en hij krijgt zijn oorspronkelijke vorm terug, dan zeggen we dat er puntsymmetrie in de figuur bestaat.
Voorbeelden van figuren die puntsymmetrie vertonen:
● Alle letters van het Engelse alfabet.
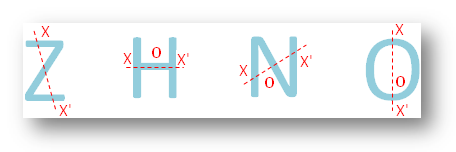
● Verschillende geometrische figuren.
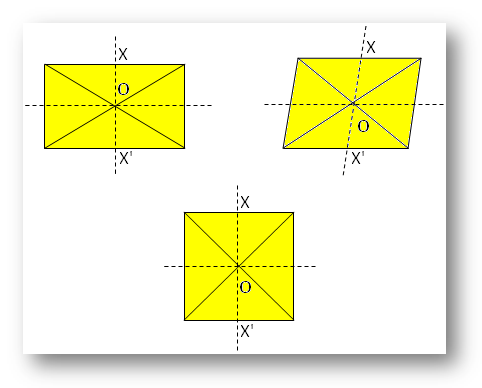
Noot:
Hier is O het centrum van symmetrie.
Ten opzichte van X bestaat er X’, zodanig dat X’ recht tegenover X staat aan de andere zijde van O.
Wat zijn de voorwaarden waaraan een vorm of figuur voldoet voor puntsymmetrie?
De voorwaarden waaraan een vorm of figuur voldoet voor puntsymmetrie, d.w.z. elk deel moet een overeenkomstig deel hebben
– de afstand moet gelijk zijn van het centrale punt
– maar moet in tegengestelde richting zijn.
● Verwante begrippen
● Lineaire symmetrie
● Symmetrielijnen
● Rotatiesymmetrie
● Volgorde van rotatiesymmetrie
● Soorten symmetrie
● Spiegeling
● Spiegeling van een punt in de x-as
● Spiegeling van een punt in de x-as
● Spiegeling van een punt in de x-as
● Spiegeling van een punt in de x-as
.as
● Spiegeling van een punt in y-as
● Spiegeling van een punt in oorsprong
● Rotatie
● 90 graden rotatie met de klok mee
● 90 graden rotatie tegen de klok in
● 180 graden rotatie
7e graad wiskundeproblemen
8e graad wiskundepraktijk
Van puntsymmetrie naar HOME PAGE