Pearson Mode Skewness

Statistiek Definities > Pearson Mode Skewness

Pearson mode skewness, ook wel Pearson’s eerste coëfficiënt van scheefheid genoemd, is een manier om de scheefheid van een verdeling te achterhalen.

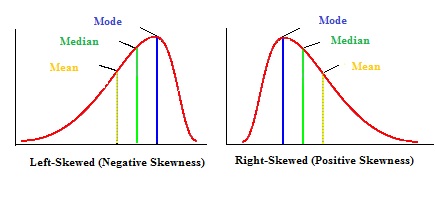
Het gemiddelde, de modus en de mediaan kunnen worden gebruikt om te achterhalen of je een positief of negatief scheve verdeling hebt.

• Als het gemiddelde groter is dan de modus, is de verdeling positief scheef.
• Als het gemiddelde kleiner is dan de modus, is de verdeling negatief scheef.
• Als het gemiddelde groter is dan de mediaan, is de verdeling positief scheef.
• Als het gemiddelde kleiner is dan de mediaan, is de verdeling negatief scheef.

Pearson-modus scheefheid

Pearson-modus scheefheid gebruikt de bovenstaande feiten om u te helpen erachter te komen of u positieve of negatieve scheefheid hebt. Als u een verdeling hebt en u kent het gemiddelde, de modus en de standaardafwijking (σ), dan is de formule voor de Pearson-modus scheefheid:

(mean-mode)/σ

Voorbeeldprobleem: U hebt gegevens met een gemiddelde van 19, een modus van 20 en een standaardafwijking van 25. Wat vertelt de Pearson Mode Skewness u over de verdeling?
(mean-mode)/σ = (19-20)/25 = -0,04.
Er is een zeer lichte negatieve scheefheid (-0,04). Opmerking: Voor de meeste doeleinden zou dit tellen als een symmetrische verdeling omdat de scheefheid zo klein is.

Pearson Mode Skewness: Alternatieve Formule.

Als je de modus niet kent, zul je de Pearson-modus scheefheid niet kunnen gebruiken. De richting van de scheefheid kan echter ook worden achterhaald door na te gaan waar het gemiddelde en de mediaan liggen. Volgens Bedrijfsstatistiek leidt dit tot een tweede, equivalente formule:

3(Gemiddelde – Mediaan) / σ

Deze formule wordt ook wel Pearson’s tweede scheefheidscoëfficiënt genoemd.

Pearson Mode Skewness: What the Results mean.

Het verschil tussen het gemiddelde en de modus, of het gemiddelde en de mediaan, vertelt je hoe ver de verdeling afwijkt van symmetrie. Een symmetrische verdeling (bijvoorbeeld de normale verdeling) heeft een scheefheid van nul.
Beide vergelijkingen geven je resultaten in standaarddeviaties, dat zijn dimensieloze meeteenheden vanaf het gemiddelde.

Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Vogt, W.P. (2005). Woordenboek van de Statistiek & Methodologie: A Nontechnical Guide for the Social Sciences. SAGE.

——————————————————————————

Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!