We zullen drie voorbeelden uit de biowetenschappen beschrijven: een uit de natuurkunde, een uit de genetica, en een uit een muizenexperiment. Ze zijn zeer verschillend, maar toch gebruiken we uiteindelijk dezelfde statistische techniek: het passen van lineaire modellen. Lineaire modellen worden gewoonlijk onderwezen en beschreven in de taal van de matrixalgebra.
Motiverende voorbeelden
Vallende voorwerpen
Stelt u zich eens voor dat u Galileo bent in de 16e eeuw, die de snelheid van een vallend voorwerp probeert te beschrijven. Een assistent beklimt de toren van Pisa en laat een bal vallen, terwijl verschillende andere assistenten de positie op verschillende tijdstippen registreren. Laten we wat gegevens simuleren met behulp van de vergelijkingen die we nu kennen en met toevoeging van wat meetfouten:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersDe assistenten overhandigen de gegevens aan Galileo en dit is wat hij ziet:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")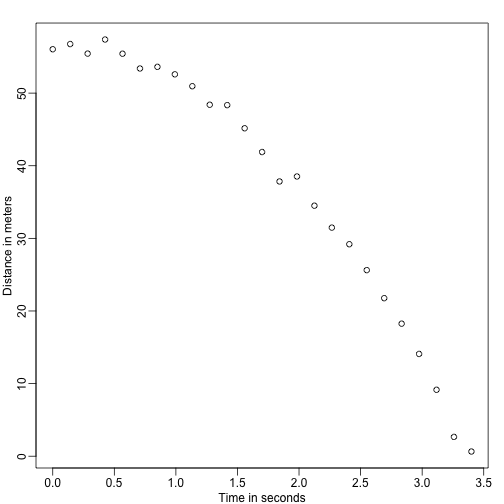
Hij kent de exacte vergelijking niet, maar uit de grafiek hierboven leidt hij af dat de positie een parabool zou moeten volgen. Dus modelleert hij de gegevens met:
With staat voor de plaats, staat voor de tijd, en houdt rekening met meetfouten. Dit is een lineair model omdat het een lineaire combinatie is van bekende grootheden (de s), die voorspellers of covariaten worden genoemd, en onbekende parameters (de s).
Vader & zoonhoogten
Stel u nu eens voor dat u Francis Galton bent in de 19e eeuw en dat u gepaarde lengtegegevens verzamelt van vaders en zonen. U vermoedt dat lengte erfelijk is. Uw gegevens:
library(UsingR)x=father.son$fheighty=father.son$sheightzien er als volgt uit:
plot(x,y,xlab="Father's height",ylab="Son's height")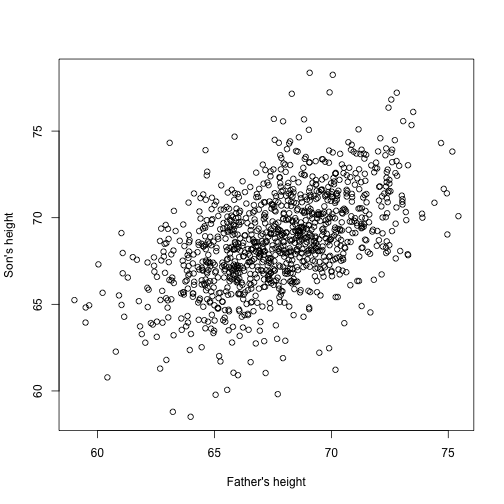
De lengte van de zonen lijkt inderdaad lineair toe te nemen met de lengte van de vaders. In dit geval is een model dat de gegevens beschrijft als volgt:
Dit is ook een lineair model met en , respectievelijk de vaders- en zoonslengte, voor het -ste paar en een term om rekening te houden met de extra variabiliteit. Hier beschouwen we de lengte van de vader als de voorspellende factor en als vast (niet willekeurig), dus gebruiken we kleine letters. Meetfouten alleen kunnen niet alle variabiliteit verklaren die in . Dit is logisch omdat er andere variabelen zijn die niet in het model zitten, bijvoorbeeld de lengte van de moeder, genetische willekeurigheid en omgevingsfactoren.
Random steekproeven uit meerdere populaties
Hier lezen we gegevens in over het lichaamsgewicht van muizen die twee verschillende diëten kregen: een vetrijk dieet en een controledieet (chow). We hebben een willekeurige steekproef van 12 muizen voor elk. Wij zijn geïnteresseerd in de vraag of het dieet een effect heeft op het gewicht. Dit zijn de gegevens:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")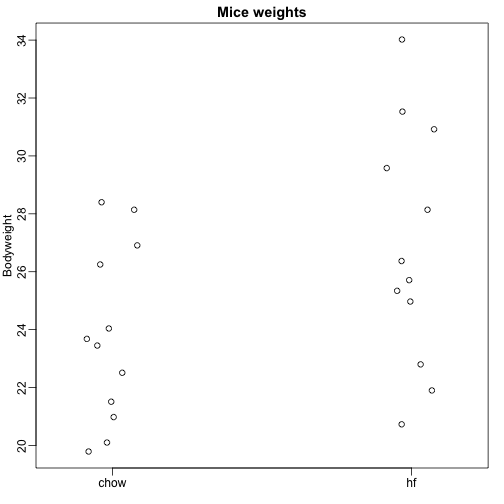
We willen het verschil in gemiddeld gewicht tussen de populaties schatten. We hebben laten zien hoe we dit kunnen doen met behulp van t-tests en betrouwbaarheidsintervallen, gebaseerd op het verschil in steekproefgemiddelden. We kunnen precies dezelfde resultaten verkrijgen met behulp van een lineair model:
met het chow-dieet gemiddelde gewicht, het verschil tussen de gemiddelden, wanneer de muis het hoog-vet (hf) dieet krijgt, wanneer hij het chow-dieet krijgt, en verklaart de verschillen tussen muizen van dezelfde populatie.
Lineaire modellen in het algemeen
We hebben drie zeer verschillende voorbeelden gezien waarin lineaire modellen kunnen worden gebruikt. Een algemeen model dat alle bovenstaande voorbeelden omvat, is het volgende:
Merk op dat we een algemeen aantal voorspellers hebben . Matrixalgebra biedt een compacte taal en een wiskundig kader om afleidingen te berekenen en te maken met elk lineair model dat in bovenstaand kader past.
Parameters schatten
Om de bovenstaande modellen bruikbaar te laten zijn, moeten we de onbekende s schatten. In het eerste voorbeeld willen we een fysisch proces beschrijven waarvoor we geen onbekende parameters kunnen hebben. In het tweede voorbeeld willen wij de erfelijkheid beter begrijpen door te schatten hoeveel de lengte van de vader gemiddeld van invloed is op de lengte van de zoon. In het laatste voorbeeld willen we bepalen of er inderdaad een verschil is: als .
De standaardbenadering in de wetenschap is de waarden te vinden die de afstand van het gepaste model tot de gegevens zo klein mogelijk maken. De volgende vergelijking wordt de vergelijking van de kleinste kwadraten (LS) genoemd en we zullen haar in dit hoofdstuk vaak tegenkomen:
Als we het minimum hebben gevonden, noemen we de waarden de kleinste kwadraten-schattingen (LSE) en duiden we ze aan met . De grootheid die men verkrijgt door de kleinste kwadratenvergelijking te evalueren aan de hand van de schattingen, noemt men de residuele som van de kwadraten (RSS). Aangezien al deze grootheden afhankelijk zijn van , zijn het willekeurige variabelen. De s zijn willekeurige variabelen en we zullen er uiteindelijk inferenties op uitvoeren.
Vallend voorwerp voorbeeld revisited
Dankzij mijn natuurkundeleraar op de middelbare school weet ik dat de vergelijking voor de baan van een vallend voorwerp is:
met respectievelijk en de starthoogte en -snelheid. De gegevens die we hierboven hebben gesimuleerd volgden deze vergelijking en voegden meetfouten toe om n waarnemingen te simuleren voor het laten vallen van de bal van de toren van Pisa . Daarom hebben we deze code gebruikt om gegevens te simuleren:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Hier ziet de data eruit met de ononderbroken lijn die de ware baan weergeeft:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)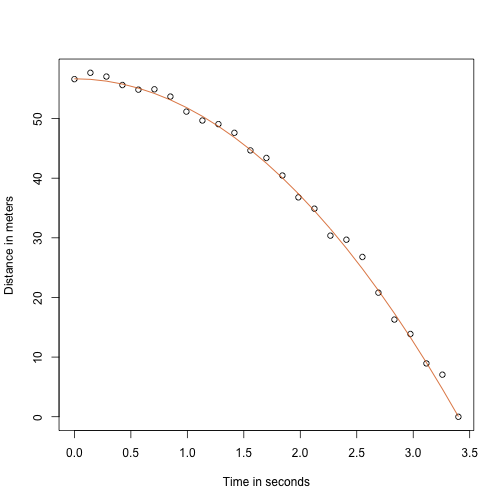
Maar we deden alsof we Galileo waren en dus kennen we de parameters in het model niet. De gegevens wijzen er wel op dat het een parabool is, dus modelleren we hem als zodanig:
Hoe vinden we de LSE?
De lm functie
In R kunnen we dit model fitten door eenvoudigweg de lm functie te gebruiken. We zullen deze functie later in detail beschrijven, maar hier is alvast een voorproefje:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Het geeft ons de LSE, evenals standaardfouten en p-waarden.
Deel van wat we in deze sectie doen, is de wiskunde achter deze functie uitleggen.
De kleinste kwadraten schatting (LSE)
Laten we een functie schrijven die de RSS berekent voor een willekeurige vector :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Zo krijgen we voor een willekeurige driedimensionale vector een RSS. Hier is een plot van de RSS als functie van wanneer we de andere twee vast houden:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)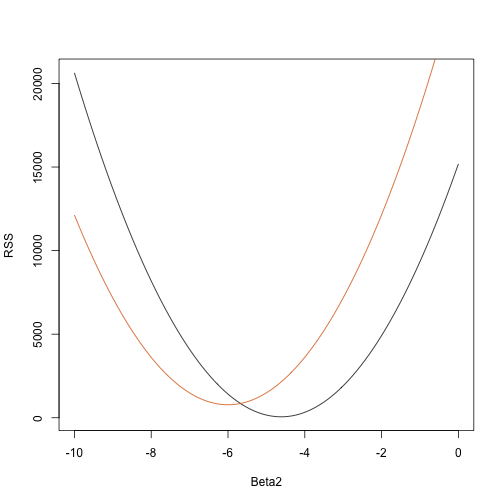
Proberen en proberen gaat hier niet werken. In plaats daarvan kunnen we gebruik maken van calculus: neem de partiële afgeleiden, stel ze op 0 en los op. Natuurlijk, als we veel parameters hebben, kunnen deze vergelijkingen nogal complex worden. Lineaire algebra biedt een compacte en algemene manier om dit probleem op te lossen.
Meer over Galton (gevorderd)
Bij het bestuderen van de vader-zoongegevens deed Galton een fascinerende ontdekking met behulp van verkennende analyse.
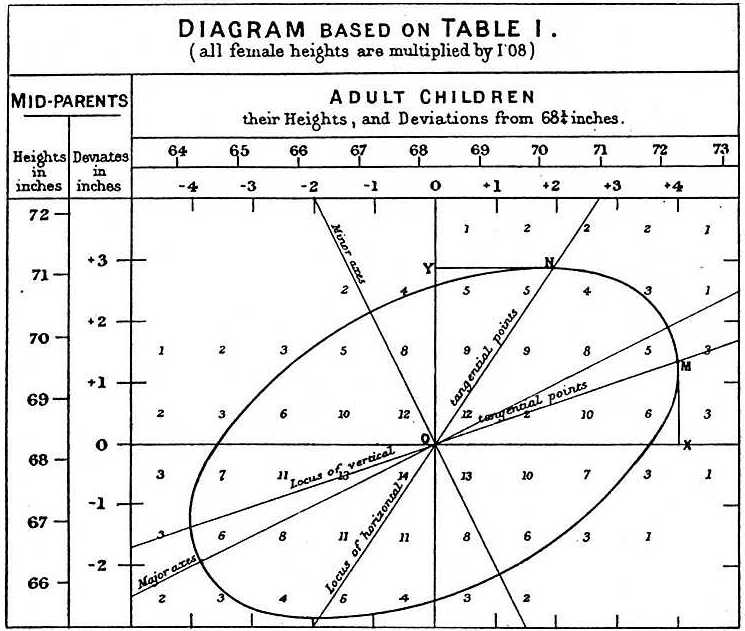
Hij merkte op dat als hij het aantal vader-zoonhoogteparen in tabelvorm opnam en alle x,y-waarden met dezelfde totalen in de tabel volgde, ze een ellips vormden. In de bovenstaande plot, gemaakt door Galton, zie je de ellips gevormd door de paren met 3 gevallen. Dit leidde vervolgens tot het modelleren van deze gegevens als gecorreleerde bivariate normaal die we eerder beschreven:
We beschreven hoe we wiskunde kunnen gebruiken om aan te tonen dat als je vasthoudt (voorwaarde om te zijn ) de verdeling van normaal verdeeld is met gemiddelde: en standaardafwijking . Merk op dat is de correlatie tussen en , wat impliceert dat als we vast , volgt in feite een lineair model. De parameters en in ons eenvoudig lineair model kunnen worden uitgedrukt in termen van , en .