Als je van een borreltje houdt, dan is een Klein flesje niet aan te bevelen. Het mag er dan vaag uitzien als een fles, maar het omsluit geen volume, wat betekent dat het geen vloeistof kan bevatten. Wat je er “in” giet, komt er gewoon weer uit.
Hoe construeer je zo’n vreemd ding en waarom zou je het willen construeren? De wiskundige Felix Klein, die de fles in 1882 ontdekte, beschreef hem als een oppervlak dat “kan worden gevisualiseerd door een stuk van een rubberen buis om te keren en door zichzelf te laten gaan, zodat buiten en binnen elkaar ontmoeten”.
Uw browser ondersteunt de videotag niet.Directe link
Het is duidelijk dat de Klein-fles, net als de meer bekende bol, een gesloten oppervlak is: het is eindig in de zin dat je het in een eindig gebied van de ruimte kunt passen, maar een mier zou er eeuwig op kunnen rondlopen zonder ooit een grens tegen te komen of over een rand te vallen. In tegenstelling tot de bol, die een binnen- en buitenkant heeft, is de Klein-fles eenzijdig: rondlopend kan onze mier beide kanten van elk punt van het oppervlak bereiken. Dit is de reden waarom de fles geen volume insluit, en het geeft ook antwoord op de “waarom” vraag: de Klein fles is interessant omdat we in de natuur niet veel eenzijdige vormen tegenkomen. (Zie hier voor een ander heel mooi plaatje van een Klein flesje.)

De Möbius strip is eenzijdig – bekijk de geanimeerde versie. (Afbeelding en animatie door Konrad Polthier.)
Als dit een beetje verwarrend is, denk dan aan een eenvoudiger voorbeeld van een eenzijdig oppervlak: de beroemde Möbiusstrip. Je kunt er een maken door twee uiteinden van een strook papier te nemen, de strook een draai te geven, en dan de uiteinden aan elkaar te lijmen. Door een strook papier te gebruiken waarvan de twee zijden verschillende kleuren hebben, bijvoorbeeld groen en oranje, kun je jezelf er gemakkelijk van overtuigen dat de resulterende Möbiusstrook eenzijdig is. Als je eenmaal gedraaid en gelijmd hebt, zul je merken dat je vanuit elk groen punt elk oranje punt kunt bereiken zonder door het papier heen te hoeven prikken of over de rand ervan te hoeven klimmen.
In tegenstelling tot de Klein-fles heeft de Möbius-strook wel een grens – die wordt gevormd door de twee niet-gelijmde randen van de oorspronkelijke strook. Maar er is een verband tussen de twee. Als je twee Möbius-stroken neemt en een gesloten vorm maakt door hun grenzen te verbinden met een gewone tweezijdige strook, zoals hieronder te zien is, dan krijg je precies de Klein-fles.
Uw browser ondersteunt de videotag niet.Directe link
-strook waarvan de achter- en voorzijden respectievelijk wit en blauw gekleurd zijn. Animatie door Konrad Polthier.
Dit feit inspireerde de wiskundige Leo Moser tot het componeren van een limerick:
Een wiskundige genaamd Klein dacht dat de Möbius band goddelijk was.Zei hij: “Als je de randen van twee aan elkaar plakt, krijg je een rare fles als de mijne.”
Sommige wiskundigen zijn echt multi-getalenteerd!
Een andere merkwaardige eigenschap van de Klein fles is dat hij zichzelf snijdt, wat betekent dat het moeilijk is om hem te maken van een enkele buis rubber, zoals Klein voorstelde. Strikt genomen is het zelfdoorsnijdende object dat hierboven is afgebeeld geen Klein fles, maar (zoals Klein aangaf) slechts een visualisatie ervan. Om te begrijpen waarom, denk eerst aan de meer bekende donut (mathematisch bekend als een torus). Je kunt een torus maken van een vierkant vel rubber door eerst twee tegenover elkaar liggende zijden tot een cilinder te lijmen, en vervolgens de twee grensdelen van die cilinder te lijmen om de torus te krijgen.

Het maken van een torus: Lijm eerst tegengestelde punten op twee tegenovergestelde zijden van het vierkant om een cilinder te maken en lijm vervolgens de twee grenscirkels van die cilinder (die overeenkomen met het lijmen van tegengestelde punten op de resterende twee zijden van het vierkant) om een torus te vormen.
Als je je niet wilt storen aan het lijmen, kun je de torus gewoon als een vierkant beschouwen, waarbij je in gedachten moet houden dat tegengestelde punten op tegenovergestelde zijden als hetzelfde worden beschouwd. Dus als je een vorm getekend op het “vierkant” over de bovenrand schuift, zal het weer verschijnen aan de onderrand en als je het over de rechterrand schuift zal het weer verschijnen aan de linkerrand (en vice versa).
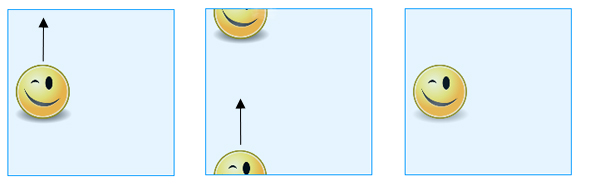
Wanneer u een op het “vierkant” getekende vorm over de bovenrand schuift, verschijnt deze weer aan de onderrand.
Om een echte Klein-fles te krijgen, begint u op dezelfde manier, met het aanwijzen van tegenover elkaar liggende punten op een paar tegenover elkaar liggende zijden van een vierkant. Identificeer voor het andere paar zijden echter geen punten die recht tegenover elkaar liggen, maar punten die diagonaal tegenover elkaar liggen, zoals in de afbeelding is te zien.
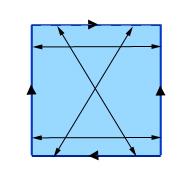
Het maken van een Klein flesje: bepaal de tegenover elkaar liggende punten van twee tegenover elkaar liggende zijden (de verticale in dit plaatje) en bepaal vervolgens de diagonaal tegenover elkaar liggende punten van de overgebleven twee zijden. (Als je de punten op de boven- en onderkant van links naar rechts labelt met de getallen 0 tot en met 1, dan wordt een punt met label x op de bovenkant geïdentificeerd met het punt met label 1-x op de onderkant.)
Het resulterende object is de Klein-fles. Je kunt het weer zien als een vierkant, waarbij je in gedachten moet houden welke grenspunten als hetzelfde worden beschouwd. Als je een vorm over een van de randen schuift waarvan de tegenoverliggende punten zijn geïdentificeerd (verticaal in ons plaatje), verschijnt hij weer aan de tegenoverliggende kant, zoals voorheen. Schuif je hem echter over een van de randen waarvan de punten diagonaal zijn geïdentificeerd (horizontaal in ons plaatje), dan verschijnt hij aan de tegenoverliggende kant, maar dan verplaatst en als spiegelbeeld van zijn oorspronkelijke zelf.
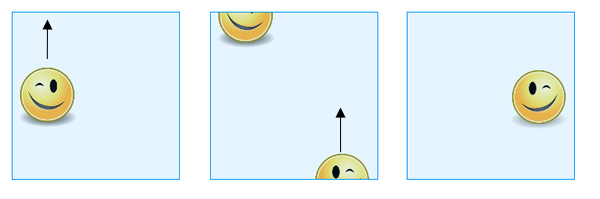
Als je een vorm over de bovenrand schuift, verschijnt hij over de onderrand, maar dan naar de andere kant en als spiegelbeeld van zijn oorspronkelijke zelf.
De enige manier om deze vorm in de driedimensionale ruimte op te bouwen door daadwerkelijk punten aan elkaar te lijmen, is door hem zichzelf te laten snijden. Dit komt neer op het identificeren van puntenparen in het binnenste van het oorspronkelijke vierkant, dus strikt genomen is de resulterende vorm niet precies hetzelfde als de Klein-fles, waarin alleen grenspunten zijn geïdentificeerd. Het is slechts één manier om de fles in de driedimensionale ruimte voor te stellen (er zijn ook andere).
Uw browser ondersteunt de videotag niet.Directe link
Spiegelbeeld en oriënteerbaarheid. Animatie door Konrad Polthier.
Vreemd genoeg zijn de begrippen “binnen”, “buiten” en “eenzijdigheid” afhankelijk van de omgevingsruimte waarin een voorwerp zich bevindt. Zo heeft een lus die op een stuk papier is getekend (in de tweedimensionale ruimte) een welbepaalde binnen- en buitenkant, maar een lus die in de driedimensionale ruimte is getekend heeft dat niet. Daarom kunnen we niet spreken van eenzijdigheid tenzij we eerst beslissen hoe we een oppervlak inbedden in de driedimensionale ruimte. Er is echter een nauw verwante eigenschap die intrinsiek is aan een vorm en niet afhangt van de omringende ruimte. Een oppervlak heet oriënteerbaar als je een erop getekende vorm niet kunt schuiven rond en terug naar waar hij begon, zodat hij eruit ziet als zijn eigen spiegelbeeld. Zoals je kunt zien in de animatie bij het plaatje rechts, is de Möbiusstrook niet oriënteerbaar. En zoals je kunt zien in het plaatje met het smiley-gezichtje hierboven, is de Klein-fles dat ook niet. Om het zijn volledige wiskundige beschrijving te geven, de Klein-fles is een gesloten, niet-oriënteerbaar oppervlak. Om er meer over te weten te komen zie het artikel Inside the Klein bottle.
Over de auteur
Marianne Freiberger is redacteur van Plus.