Voordat we beginnen, moeten we enkele aannames doen.
In de eerste plaats werken we met Newtonse vloeistoffen. Dit is de eenvoudigste wiskundige manier om rekening te houden met de viscositeit in een vloeistof. Er zijn geen echte vloeistoffen die perfect onder deze categorie vallen, maar in de meeste gevallen kunnen lucht en water worden behandeld als een Newtonse vloeistof. De andere zeer belangrijke hypothese die we maken is dat de vloeistof onsamendrukbaar is. Dit betekent dat de dichtheid, rho, een constante is.
Massabehoud

De eerste vergelijking vertelt ons dat de massa van de vloeistof waar we mee bezig zijn, behouden blijft. De vloeistof kan van vorm veranderen, maar deze vergelijking vertelt ons dat de massa van begin tot eind hetzelfde blijft.
Nog even over wiskunde. De letter u stelt de snelheid van de vloeistof voor en het is een vector. Hij heeft drie componenten, we kunnen ze u, v, w noemen en ze stellen de snelheid van de vloeistof voor in de x-, y- en z-richting. De griekse letter nabla ∇ gevolgd door een punt is de divergentie-operator. Dit betekent dat we de componenten ervan in elke richting (in dit geval x, y, z) moeten differentiëren.

De eerste afgeleide vertelt ons hoe de x-component van de snelheid verandert als we in de x-richting bewegen. Hetzelfde geldt voor de andere twee afgeleiden. Omdat deze vergelijking gelijk is aan nul, toont ze ons dat de massa behouden blijft.
Behoud van momentum

De tweede vergelijking is eigenlijk een verzameling van drie differentiaalvergelijkingen. Deze kan worden beschreven als de tweede wet van Newton voor de vloeistoffen. Als we de uitdrukking uitbreiden krijgen we een complex stelsel.
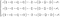
Omdat het een stuk eenvoudiger te begrijpen is, gaan we ons concentreren op het niet-geëxpandeerde behoud van momentum.
Wanneer we met vloeistoffen werken, kunnen we zeggen dat massa en dichtheid dezelfde dingen zijn (zolang het volume hetzelfde is). Als we twee vloeistoffen beschouwen, kunnen we zeggen dat de dichtste vloeistof de “zwaardere” is (b.v. kwik en water). In dit geval is de griekse letter ρ (rho) de dichtheid van de vloeistof.
We hebben de massa, nu hebben we om terug te keren naar de tweede wet van Newton de versnelling nodig. Dat is precies het resultaat van de tijdsafgeleide van de snelheidsvector.

Nu hebben we alleen nog de termen aan de rechterkant van het gelijkheidsteken, en die vertegenwoordigen alle krachten die op de vloeistof worden uitgeoefend.
De eerste term ∇p is de gradiënt van de druk. Zij vertegenwoordigt het drukverschil in de ruimte waar de vloeistof zich bevindt. Als er bijvoorbeeld een zone is met een lage druk en een andere met een hogere druk, zal de vloeistof zich verplaatsen van de sectie met de hoge druk naar de lagere sectie. De gradiënt van p zegt dat allemaal.
De tweede term beschrijft de viscositeit van de vloeistof. Denk aan twee verschillende vloeistoffen, zoals water en honing. Als je een glas water inschenkt, valt het snel en gemakkelijk. Als je hetzelfde doet met honing, is het kleverig en giet het heel langzaam. Dat is wat die uitdrukking zegt.
De laatste term, F, is de gemakkelijkste, omdat hij alle externe krachten weergeeft die op die vloeistof kunnen worden uitgeoefend. Meestal is de kracht die we hier beschouwen de zwaartekracht.
Dit is het, al die mooie symbolen en letters betekenen gewoon kracht = massa x versnelling.
Gebruik van de Navier-Stokes vergelijkingen
Omdat het oplossen van deze vergelijkingen zo ingewikkeld is, moeten we om ze te gebruiken een heleboel benaderingen maken. Enkele voorbeelden zijn de Poiseuille- en de Couette-stroming. Met veel aannames konden deze twee wetenschappers een oplossing vinden voor de Navier-Stokes vergelijkingen voor een zeer specifieke toepassing. Als we ze echter willen gebruiken voor een meer gecompliceerde taak, zoals de weersvoorspellingen, moeten we iets anders doen.
De meest gebruikelijke manier om deze vergelijkingen te gebruiken is door ze te transformeren, met het Reynolds-gemiddelde. Dit is een geavanceerd wiskundig proces en de resultaten zijn de Reynolds-vergelijkingen. Ze worden gewoonlijk RANS-vergelijkingen (Reynolds average Navier-Stokes) genoemd.
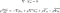
Deze vergelijkingen worden gebruikt wanneer de vloeistof zich in een turbulente stroming bevindt. Ze lijken bijna precies op de Navier-Stokes vergelijkingen, behalve de laatste term. Deze wordt de Reynolds-spanningstensor genoemd. Het is de grootheid die ons in staat stelt rekening te houden met de turbulentie in de vloeistof.
In de RANS-vergelijkingen worden de grootheden die we gebruiken gemiddeld over een tijdsinterval. Dit interval moet klein genoeg zijn om de waarneming van het fenomeen dat wij bestuderen mogelijk te maken. Tegelijkertijd moet het groot genoeg zijn om het turbulentie-effect aan belang te laten inboeten.
Met de juiste aannames werken deze vergelijkingen. We weten hoe we ze kunnen gebruiken om F1-auto’s sneller te maken, om een ruimteschip naar het ISS te brengen en om het weerbericht te maken. Dus u vraagt zich misschien af waarom het bewijs van deze vergelijkingen een miljoen dollar waard is?
Een prijs van een miljoen dollar
Vanuit natuurkundig oogpunt zijn deze vergelijkingen gewoon de tweede wet van Newton die werkt met vloeistoffen. Met wat aannames en vereenvoudigingen kunnen we verbazingwekkende dingen doen.
Het echte probleem is dit. Het oplossen van deze vergelijkingen zonder benaderingen is gewoon vreselijk ingewikkeld. Het is zo moeilijk dat het nog niet bewezen is dat de oplossingen echt bestaan. En dit is waar de Millenniumprijs om de hoek komt kijken.
De officiële probleemstelling (hier te vinden) luidt:
Bewijs of geef een tegenvoorbeeld van de volgende stelling: in drie ruimtedimensies en tijd, gegeven een initieel snelheidsveld, bestaan er een vectorsnelheids- en een scalair drukveld, die beide glad en globaal gedefinieerd zijn, die de Navier-Stokes-vergelijkingen oplossen.
Wat dit betekent is dat je, om de prijs te winnen, drie dingen moet doen:
- Bewijzen dat er een oplossing bestaat
- De oplossing moet in elk punt van de ruimte bestaan
- De oplossing moet glad zijn. Dit betekent dat een kleine verandering in de beginvoorwaarden slechts een kleine variatie van het resultaat oplevert.
Voor een ingenieur is het meestal voldoende om te weten dat deze vergelijkingen werken, al is het maar tot op een bepaald niveau van benadering. Voor een wiskundige is het echter van groot belang te weten of de oplossingen bestaan en hoe zij zich gedragen.
U denkt nu misschien dat als zij werken zoals zij werken, het verspillen van tijd en energie aan het zoeken naar een bewijs een totale tijdverspilling is. Welnu, zoals bij veel technologische vorderingen in de geschiedenis van de mensheid lijkt het resultaat misschien niet erg belangrijk. Wat belangrijk is, is de weg ernaartoe, die nieuwe kennis en verbeteringen in ons leven kan brengen.
Denk aan ruimtemissies. Als de mens nooit had besloten om op de maan te gaan lopen, zouden we niet veel voorwerpen hebben die worden gebruikt om ons leven te verbeteren. MRI-machines en pacemakers zijn afkomstig van technologieën die voor ruimte-exploratie zijn ontwikkeld. Vandaag gebruiken dokters over de hele wereld ze elke dag om levens te redden. Hetzelfde geldt hier. De weg naar de oplossing van de Navier-Stokes-vergelijkingen zal ons helpen om ons begrip van vloeistoffen en meer te verbeteren. Het kan ons tot nieuwe ontdekkingen brengen en zal waarschijnlijk de uitvinding van nieuwe wiskunde vereisen. Deze kan dan worden gebruikt om vele andere problemen op te lossen, om nieuwe technologieën uit te vinden om ons leven te verbeteren en ons beter te maken.