Construct Equilateral Triangle – MathBitsNotebook (Geo

Equilateral Triangle MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits’ Teacher Resources Terms of Use Contact Person: Donna Roberts

Gebruik alleen je passer en je rechte rand bij het tekenen van een constructie. Geen tekeningen uit de vrije hand!

We gaan DRIE constructies maken van een gelijkzijdige driehoek. De eerste is het construeren van een gelijkzijdige driehoek gegeven de lengte van een zijde, en de andere twee zijn het construeren van een gelijkzijdige driehoek ingeschreven in een cirkel.

Gegeven: de lengte van één zijde van de driehoek Construeer: een gelijkzijdige driehoek

STappen:
1. Plaats uw kompaspunt op A en meet de afstand tot punt B. Zwaai een boog van deze grootte boven (of onder) het lijnstuk.
2. Zonder de spanwijdte op het kompas te veranderen, plaatst u de kompaspunt op B en zwaait u dezelfde boog, die de eerste boog snijdt.
3. Label het snijpunt als het derde hoekpunt van de gelijkzijdige driehoek.

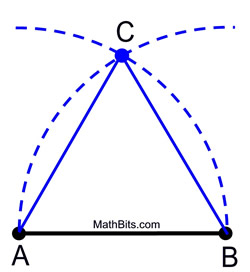Zie de volledige cirkels aan het werk.

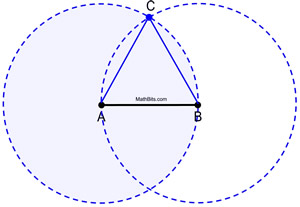
Bewijs van constructie: Cirkel A is congruent met cirkel B, omdat ze elk gevormd zijn met dezelfde straallengte, AB. Omdat AB en AC de lengtes van de stralen van cirkel A zijn, zijn ze aan elkaar gelijk. Evenzo zijn AB en BC stralen van cirkel B, en zijn zij gelijk aan elkaar. Daarom is AB = AC = BC door substitutie (of transitieve eigenschap). Aangezien congruente segmenten even lang zijn, en ΔABC gelijkzijdig is (met drie congruente zijden).

STappen:
1. Plaats je passerpunt op het papier en teken een cirkel. (Houd deze passer overspannen!)
2. Plaats een punt, met het label A, ergens op de omtrek van de cirkel om als beginpunt te dienen.
3. Zonder de spanwijdte van het kompas te veranderen, plaats de kompaspunt op A en maak een kleine boog over de omtrek van de cirkel.
4. Zonder de spanwijdte van het kompas te veranderen, verplaats de kompaspunt naar het snijpunt van de vorige boog en de omtrek en maak nog een kleine boog over de omtrek van de cirkel.
5. Blijf dit proces van “stappen” rond de cirkel herhalen totdat u terugkeert naar punt A.
6. Begin bij A en verbind elke andere boog op de cirkel om de gelijkzijdige driehoek te vormen.

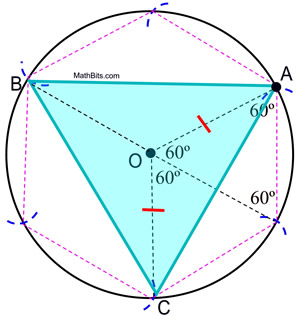Raadpleeg het bewijs van een ingeschreven regelmatige zeshoek voor meer informatie over het bewijs van deze constructie.

Bewijs van de constructie: Het bewijs van de ingeschreven regelmatige zeshoek toont aan dat de centrale hoeken van een regelmatige zeshoek 60º bevatten. De centrale hoeken van de driehoek ingeschreven in deze cirkel bevatten 120º. Aangezien ΔAOC gelijkbenig is (OA en OC zijn stralen), geldt m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA door SAS. Door CPCTC is ∠OCB ∠OCA en m∠OCB = 30º door substitutie en m∠BCA = 60º. Op dezelfde manier hebben we m∠ACB = m∠CBA = m∠BAC = 60º en de gelijkzijdige ΔABC.

STAPPEN:
1. Plaats je passerpunt op het papier en teken een cirkel, O. (Houd deze passeroverspanning aan!)
2. Teken met behulp van een liniaal een middellijn van de cirkel, waarbij je de eindpunten P en B labelt.
3. Plaats, zonder de overspanning van het kompas te veranderen, de passerpunt op P en teken een volledige cirkel.
4. Label de snijpunten van de twee cirkelomtrekken met A en C.
5. Teken lijnstukken van A naar B, B naar C en C naar A, om de gelijkzijdige driehoek te vormen.

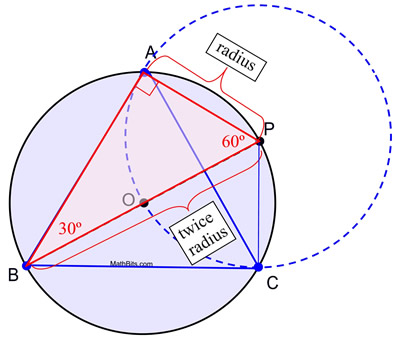
Bewijs van constructie: Deze constructie maakt gebruik van het feit dat een hoek ingeschreven in een halve cirkel een rechte hoek is, en dat in een 30º-60º-90º driehoek de lengte van het korte been de helft is van de lengte van de schuine zijde. In deze constructie zijn cirkel O en cirkel P congruent, omdat ze dezelfde straallengte hebben. AP is een straallengte van cirkel P en straal AP = OP. OP is ook een straallengte van cirkel O (samen met OB) en diameter BP = BO + OP = 2 OP. Door substitutie wordt BP = 2 AP, waarmee de voorwaarden zijn geschapen voor m∠ABP = 30º. Bijgevolg is m∠APB = 60º. Met een gelijksoortige redenering kan voor ΔPBC worden vastgesteld dat m∠PBC = 30º en m∠BPC = 60º waardoor ΔPBC ΔPBA door ASA (met gemeenschappelijke zijde van B naar P).
Nu, aangezien het de overeenkomstige zijden zijn van de twee congruente driehoeken, maakt ΔABC gelijkbenig. ∠BAC ∠BCA omdat de basishoeken van een gelijkbenige driehoek congruent zijn.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º door Angle Addition Postulate en substitutie. m∠BAC + m∠BCA + m∠ABC = 180º omdat de som van de hoekmaten in een driehoek 180º is. Omdat m∠BAC + m∠BAC + 60º = 180º door substitutie, weten we dat 2m∠BAC = 120º en m∠BAC = 60º. Bijgevolg is m∠BCA ook gelijk aan 60º door substitutie, zodat ΔABC gelijkzijdig is.