We kunnen Gibbs-Helmholtz gebruiken om de temperatuurafhankelijkheid van (K)
}{∂T}
Bij evenwicht kunnen we (Δ_rG^o) gelijkstellen aan (-RT\ln K) zodat we krijgen:
}{∂T} \_P = \dfrac{Δ_rH^o}{RT^2}
We zien dat het toe- of afnemen van de reactie-enthalpie met de temperatuur samenhangt met het positief of negatief zijn van de reactie-enthalpie. Als de temperatuur zo weinig verandert dat Δ_rH^o als constant kan worden beschouwd, kunnen we een waarde van Δ(K) bij de ene temperatuur omzetten in een andere door bovenstaande uitdrukking te integreren, we krijgen dan een soortgelijke afleiding als bij smeltpuntdepressie:
Als er meer nauwkeurigheid nodig is, kunnen we corrigeren voor de temperatuurveranderingen van ΔrHo door gegevens over de warmtecapaciteit te gebruiken.
Hoeveel ΔrHo met de temperatuur toe- of afneemt, hangt samen met het feit of de reactie-enthalpie positief of negatief is.
De uitdrukking voor (K) is een tamelijk gevoelige functie van de temperatuur gezien de exponentiële afhankelijkheid van het verschil tussen de stoichiometrische coëfficiënten Een manier om de gevoelige temperatuurafhankelijkheid van evenwichtsconstanten te zien is door eraan te herinneren dat
Hoewel, omdat onder constante druk en temperatuur
Vergelijking \(\ref{18}\) wordt
Door de natuurlijke log van beide zijden te nemen, krijgen we een lineair verband tussen \(\ln K \) en de standaard enthalpie¨en entropie¨en:
, die bekend staat als de van’t Hoff-vergelijking. Hieruit blijkt dat een plot van \(\ln K\) tegen \(1/T) een lijn moet zijn met een helling \(-Delta_r{H^o}/R\) en een intercept \(\Delta_r{S^o}/R\).
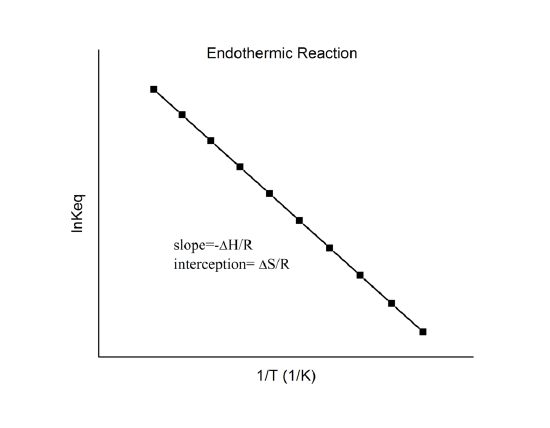
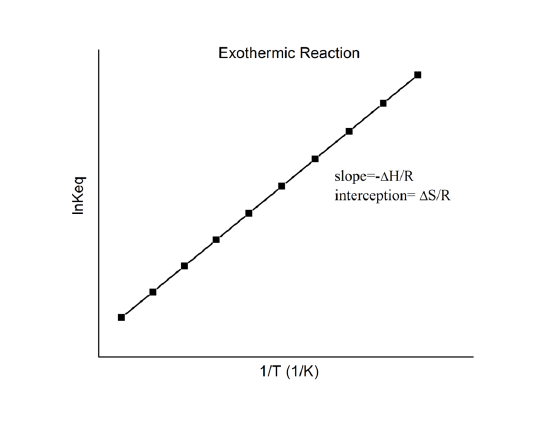
Hiermee kunnen deze grootheden worden bepaald uit de gegevens van \(\ln K\) vs. \(1/T\) zonder calorimetrie uit te voeren. Natuurlijk is de belangrijkste aanname hier dat \Delta_r{H^o}\) en \Delta_r{S^o}\) slechts zeer zwak afhankelijk zijn van \(T^o}), wat meestal het geval is.