Než začneme, musíme učinit několik předpokladů.
Předně pracujeme s newtonovskými tekutinami. To je nejjednodušší matematický způsob, jak zohlednit viskozitu tekutiny. Neexistují skutečné kapaliny, které by dokonale spadaly do této kategorie, ale ve většině případů lze vzduch a vodu považovat za newtonovskou kapalinu. Další velmi důležitou hypotézou, kterou vyslovujeme, je, že tekutina je nestlačitelná. To znamená, že její hustota, rho, je konstantní.
Zachování hmotnosti

První rovnice nám říká, že hmotnost tekutiny, se kterou pracujeme, se zachovává. Kapalina může měnit svůj tvar, ale tato rovnice nám říká, že hmotnost je od začátku do konce stejná.
Teď si povíme něco o matematice. Písmeno u představuje rychlost kapaliny a je to vektor. Má tři složky, můžeme je nazvat u, v, w a představují rychlost kapaliny ve směru x, y a z. V tomto případě se jedná o vektor. Řecké písmeno nabla ∇ následované tečkou je operátor divergence. To znamená, že musíme diferencovat její složky v každém směru (v tomto případě x, y, z).

První derivace nám říká, jak se mění složka rychlosti x při pohybu po směru x. V tomto případě se jedná o derivaci vektoru rychlosti. Totéž platí pro další dvě derivace. Protože je tato rovnice rovna nule, ukazuje nám, že hmotnost se zachovává.
Zachování hybnosti

Druhá rovnice je vlastně souborem tří diferenciálních rovnic. Tu lze popsat jako druhý Newtonův zákon pro tekutiny. Pokud výraz rozšíříme, dostaneme složitou soustavu.
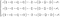
Protože je to mnohem jednodušší na pochopení, budeme se věnovat zachování hybnosti nerozšířené.
Při práci s tekutinami můžeme říci, že hmotnost a hustota jsou totéž (pokud je jejich objem stejný). Pokud uvažujeme dvě kapaliny, můžeme říci, že hustší je ta „těžší“ (např. rtuť a voda). V tomto případě je řecké písmeno ρ (rho) hustotou kapaliny.
Máme hmotnost, nyní, abychom se vrátili k druhému Newtonovu zákonu, potřebujeme zrychlení. To je právě výsledkem časové derivace vektoru rychlosti.

Teď už nám zbývají jen členy na pravé straně znaménka rovnosti, a ty představují všechny síly, které na tekutinu působí.
První člen ∇p je gradient tlaku. Představuje rozdíl tlaků v prostoru, kde se kapalina nachází. Pokud se například nachází oblast s nízkým tlakem a další s vyšším tlakem, bude se kapalina pohybovat z části s vysokým tlakem do části s nižším tlakem. To vše říká gradient p.
Druhý člen popisuje viskozitu kapaliny. Představte si dvě různé kapaliny, například vodu a med. Když nalijete sklenici vody, rychle a snadno opadá. Když totéž uděláte s medem, je lepkavý a nalévá se velmi pomalu. To říká tento výraz.
Poslední člen, F, je nejjednodušší, protože představuje všechny vnější síly, které mohou na tuto kapalinu působit. Obvykle zde uvažujeme sílu gravitační.
To je ono, všechny ty fantastické symboly a písmenka znamenají prostě síla = hmotnost x zrychlení.
Použití Navierových-Stokesových rovnic
Protože řešení těchto rovnic je tak složité, abychom je mohli použít, musíme provést mnoho aproximací. Jako příklad lze uvést Poiseuillovo a Couettovo proudění. Tito dva vědci dokázali s mnoha předpoklady najít řešení Navierových-Stokesových rovnic pro velmi specifickou aplikaci. Pokud je však chceme použít pro složitější úlohu, jako je předpověď počasí, musíme udělat něco jiného.
Nejběžnějším způsobem, jak tyto rovnice použít, je jejich transformace, a to pomocí Reynoldsova průměru. Jedná se o pokročilý matematický postup a výsledkem jsou Reynoldsovy rovnice. Obvykle se nazývají RANS (což znamená Reynoldsovy zprůměrované Navier-Stokesovy rovnice).
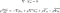
Tyto rovnice se používají, pokud se tekutina nachází v turbulentním proudění. Vypadají téměř stejně jako Navierovy-Stokesovy rovnice, s výjimkou posledního členu. Ten se nazývá Reynoldsův tenzor napětí. Je to veličina, která nám umožňuje zohlednit turbulenci v tekutině.
V rovnicích RANS jsou veličiny, které používáme, zprůměrovány na časovém intervalu. Tento interval musí být dostatečně malý, aby umožnil pozorování jevu, který studujeme. Zároveň musí být dostatečně velký, aby vliv turbulence ztratil na významu.
Při správných předpokladech tyto rovnice fungují. Víme, jak je použít k tomu, aby byly vozy F1 rychlejší, aby se kosmická loď dostala na ISS a aby se dala předpovědět předpověď počasí. Možná se tedy ptáte, proč má důkaz těchto rovnic cenu milionu dolarů?
Cena milion dolarů
Z fyzikálního hlediska jsou tyto rovnice jen druhým Newtonovým zákonem, který pracuje s kapalinami. Když přijmeme určité předpoklady a zjednodušení, můžeme s nimi dělat úžasné věci.
Skutečný problém je tento. Řešení těchto rovnic bez aproximací je prostě strašně složité. Je to tak složité, že se nepodařilo dokázat, že řešení skutečně existují. A tady přichází na řadu Cena tisíciletí.
Oficiální zadání problému (najdete ho zde) zní:
Dokažte nebo uveďte protipříklad následujícího tvrzení: Ve třech prostorových rozměrech a čase existuje při daném počátečním rychlostním poli vektorová rychlost a skalární tlakové pole, které jsou hladké a globálně definované a které řeší Navierovy-Stokesovy rovnice.
To znamená, že k získání ceny musíte udělat tři věci:
- Dokázat, že řešení existuje
- Řešení musí existovat v každém bodě prostoru
- Řešení musí být hladké. To znamená, že malá změna počátečních podmínek způsobí jen malou změnu výsledku
Pro inženýra obvykle stačí vědět, že tyto rovnice fungují, i když jen na určité úrovni přiblížení. Přesto je pro matematika velmi důležité vědět, zda řešení existují a jak se chovají.
Možná si teď říkáte, že pokud fungují tak, jak jsou, je vynakládání času a energie na hledání důkazu naprostou ztrátou času. No, stejně jako u mnoha technologických pokroků v historii lidstva se výsledek nemusí zdát příliš důležitý. Důležitá je cesta k němu, která může přinést nové poznatky a zlepšení našeho života.
Přemýšlejte o vesmírných misích. Kdyby se lidé nikdy nerozhodli jít a projít se po Měsíci, neměli bychom mnoho předmětů, které slouží ke zlepšení našeho života. Přístroje magnetické rezonance a kardiostimulátory pocházejí z technologií vyvinutých pro výzkum vesmíru. Dnes je lékaři po celém světě denně používají k záchraně životů. Totéž platí i zde. Cesta k objevení řešení Navierových-Stokesových rovnic nám pomůže zlepšit naše chápání nejen tekutin. Může nás přivést k novým objevům a pravděpodobně bude vyžadovat vynález nové matematiky. Ta pak může být použita k zodpovězení mnoha dalších problémů, k vynalezení nových technologií, které zlepší náš život a učiní nás lepšími.