Popíšeme tři příklady z přírodních věd: jeden z fyziky, jeden z genetiky a jeden z pokusu na myši. Jsou velmi odlišné, přesto nakonec použijeme stejnou statistickou techniku: fitování lineárních modelů. Lineární modely se obvykle vyučují a popisují v jazyce maticové algebry.
Motivační příklady
Padající objekty
Představte si, že jste Galileo v 16. století a snažíte se popsat rychlost padajícího objektu. Asistent vyleze na věž v Pise a upustí kuličku, zatímco několik dalších asistentů zaznamenává polohu v různých časech. Nasimulujme si nějaká data pomocí rovnic, které známe dnes, a přidejme nějakou chybu měření:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersAsistenti předají data Galileovi a ten vidí toto:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")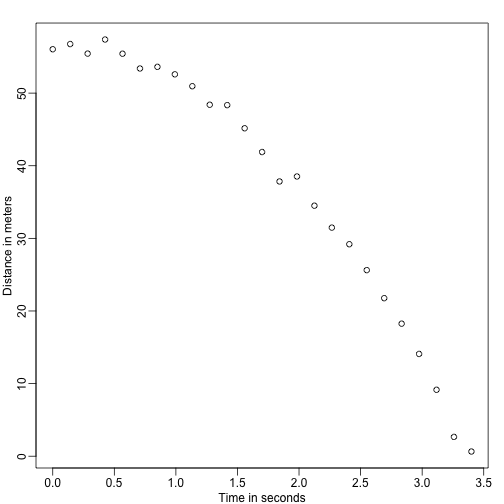
Přesnou rovnici nezná, ale pohledem na výše uvedený graf odvodí, že poloha by měla sledovat parabolu. Modeluje tedy data pomocí:
S reprezentující polohu, reprezentující čas a zohledňující chybu měření. Jedná se o lineární model, protože jde o lineární kombinaci známých veličin (th s) označovaných jako prediktory nebo kovariáty a neznámých parametrů (the s).
Výška otce & syna
Teď si představte, že jste Francis Galton v 19. století a shromažďujete párová data o výšce otců a synů. Máte podezření, že výška je dědičná. Vaše data:
library(UsingR)x=father.son$fheighty=father.son$sheightvypadají takto:
plot(x,y,xlab="Father's height",ylab="Son's height")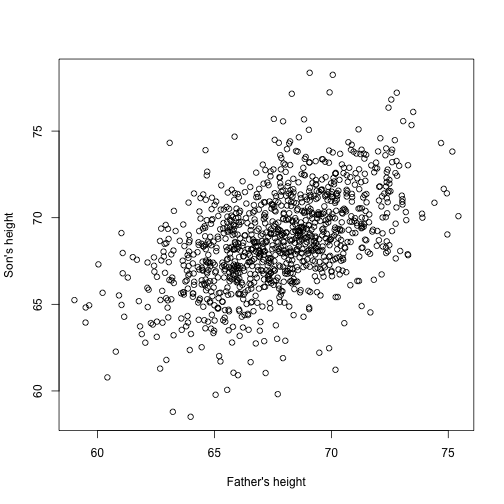
Výšky synů skutečně zřejmě lineárně rostou s výškami otců. V tomto případě je model, který popisuje data, následující:
Toto je také lineární model s a , výškami otce a syna, resp. pro -tý pár a členem, který zohledňuje dodatečnou variabilitu. Zde uvažujeme o výškách otců jako o prediktoru a o tom, že jsou fixní (nikoliv náhodné), takže používáme malá písmena. Samotná chyba měření nemůže vysvětlit veškerou variabilitu pozorovanou v . To dává smysl, protože existují další proměnné, které v modelu nejsou, například výška matek, genetická náhodnost a faktory prostředí.
Náhodné vzorky z více populací
Zde čteme údaje o tělesné hmotnosti myší, které byly krmeny dvěma různými dietami: s vysokým obsahem tuku a kontrolní (chow). Pro každou z nich máme náhodný vzorek 12 myší. Zajímá nás, zda má strava vliv na hmotnost. Zde jsou data:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")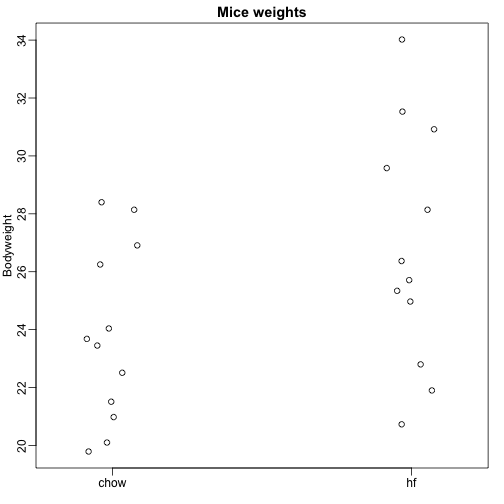
Chceme odhadnout rozdíl v průměrné hmotnosti mezi populacemi. Ukázali jsme si, jak to provést pomocí t-testů a intervalů spolehlivosti na základě rozdílu průměrů vzorků. Přesně stejné výsledky můžeme získat pomocí lineárního modelu:
s průměrnou hmotností chow stravy, rozdílem mezi průměry, kdy myš dostane stravu s vysokým obsahem tuku (hf), kdy dostane stravu chow, a vysvětlí rozdíly mezi myšmi stejné populace.
Lineární modely obecně
Viděli jsme tři velmi odlišné příklady, kdy lze lineární modely použít. Obecný model, který zahrnuje všechny výše uvedené příklady, je následující:
Všimněte si, že máme obecný počet prediktorů . Maticová algebra poskytuje kompaktní jazyk a matematický rámec pro výpočet a odvození s jakýmkoli lineárním modelem, který zapadá do výše uvedeného rámce.
Odhad parametrů
Pro užitečnost výše uvedených modelů musíme odhadnout neznámé s. V prvním příkladu chceme popsat fyzikální proces, pro který nemůžeme mít neznámé parametry. Ve druhém příkladu lépe pochopíme dědičnost tím, že odhadneme, jak moc v průměru ovlivňuje výška otce výšku syna. V posledním příkladu chceme určit, zda skutečně existuje rozdíl: pokud .
Standardním přístupem ve vědě je najít hodnoty, které minimalizují vzdálenost fitovaného modelu od dat. Následující rovnice se nazývá rovnice nejmenších čtverců (LS) a v této kapitole se s ní budeme často setkávat:
Jakmile najdeme minimum, budeme hodnoty nazývat odhady nejmenších čtverců (LSE) a označovat je . Veličina získaná při vyhodnocení rovnice nejmenších čtverců na odhadech se nazývá reziduální součet čtverců (RSS). Protože všechny tyto veličiny závisí na , jsou to náhodné veličiny. Veličiny s jsou náhodné veličiny a nakonec na nich budeme provádět inferenci.
Příklad s padajícím objektem znovu
Díky svému učiteli fyziky na střední škole vím, že rovnice pro trajektorii padajícího objektu je:
s a počáteční výškou, resp. rychlostí. Data, která jsme simulovali výše, se řídila touto rovnicí a přidali jsme chybu měření, abychom simulovali n pozorování pro pád míče z věže v Pise . Proto jsme k simulaci dat použili tento kód:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Tady vypadají data s plnou čarou představující skutečnou trajektorii:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)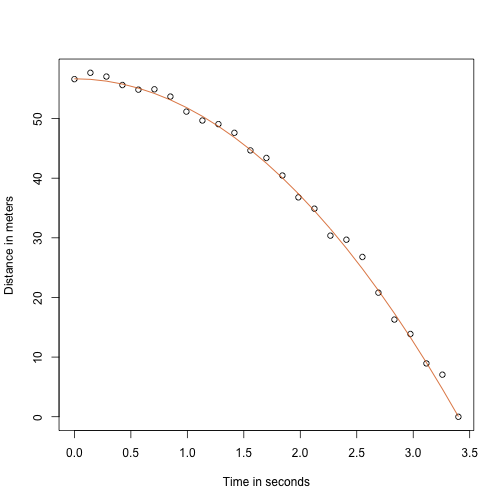
Ale my jsme předstírali, že jsme Galileo, a proto neznáme parametry modelu. Data ale naznačují, že jde o parabolu, takže ji jako takovou namodelujeme:
Jak zjistíme LSE?
Funkce lm
V R můžeme tento model fitovat jednoduše pomocí funkce lm. Tuto funkci si podrobně popíšeme později, ale zde je její náhled:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Dává nám LSE, stejně jako standardní chyby a p-hodnoty.
Částečně si v této části vysvětlíme matematické pozadí této funkce.
Odhad nejmenších čtverců (LSE)
Napíšeme funkci, která vypočítá RSS pro libovolný vektor :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Tak pro libovolný třírozměrný vektor dostaneme RSS. Zde je graf RSS jako funkce, kdy ostatní dva vektory ponecháme pevné:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)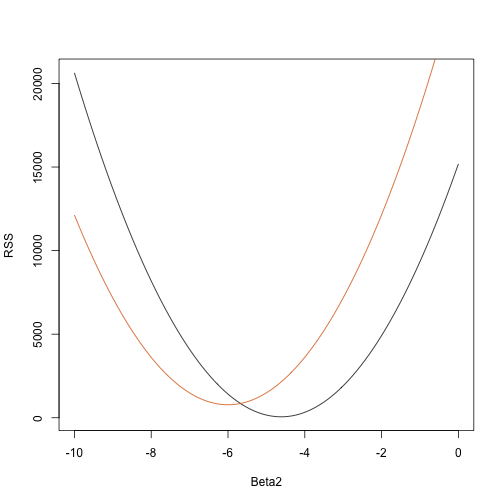
Tady pokus a omyl nebude fungovat. Místo toho můžeme použít výpočet: vezmeme parciální derivace, nastavíme je na 0 a vyřešíme. Samozřejmě pokud máme mnoho parametrů, mohou být tyto rovnice poměrně složité. Lineární algebra poskytuje kompaktní a obecný způsob řešení tohoto problému.
Další o Galtonovi (pro pokročilé)
Při studiu údajů o výšce otce a syna učinil Galton fascinující objev pomocí explorační analýzy.
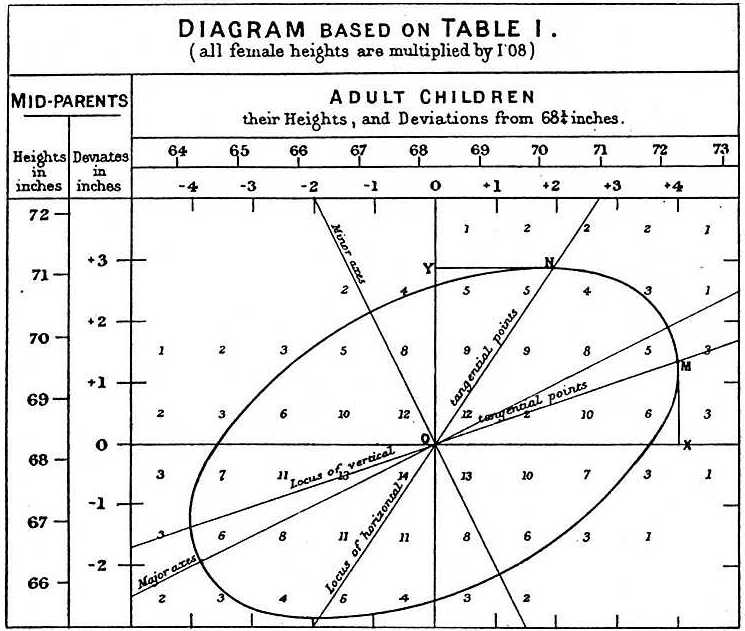
Všiml si, že pokud sestavil tabulku počtu výškových dvojic otce a syna a sledoval v ní všechny hodnoty x,y, které měly stejné součty, tvořily elipsu. Na výše uvedeném grafu, který vytvořil Galton, vidíte elipsu vytvořenou dvojicemi, které mají 3 případy. To pak vedlo k modelování těchto dat jako korelovaných dvourozměrných normálních, které jsme popsali dříve:
Popsali jsme, jak můžeme pomocí matematiky ukázat, že pokud zachováme fixní (podmínku, aby bylo ) rozdělení je normálně rozdělené se střední hodnotou: a směrodatnou odchylkou . Všimněte si, že je korelace mezi a , což znamená, že pokud zafixujeme , skutečně se řídí lineárním modelem. Parametry a v našem jednoduchém lineárním modelu lze vyjádřit pomocí , a .
.