Konstrukce rovnostranného trojúhelníku – MathBitsNotebook (Geo

Rovnostranný trojúhelník MathBitsNotebook.com Topická osnova | Osnova geometrie | MathBits‘ Teacher Resources Podmínky použití Kontaktní osoba: Donna Roberts

Při rýsování konstrukce používejte pouze kružítko a pravítko. Žádné kreslení volnou rukou!!!

Budeme dělat TŘI konstrukce rovnostranného trojúhelníku. První bude sestrojení rovnostranného trojúhelníku daného délkou jedné strany a další dvě budou sestrojení rovnostranného trojúhelníku vepsaného do kružnice.

Dáno: délka jedné strany trojúhelníku Konstruuj: rovnostranný trojúhelník

KROKY:
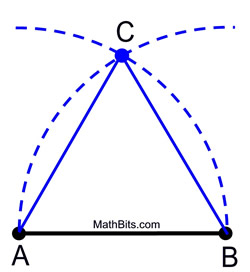
1. Délka jedné strany trojúhelníku vepsaného do kruhu. Umístěte bod kompasu na bod A a změřte vzdálenost k bodu B. Nad úsečkou (nebo pod ní) vykružte oblouk této velikosti.
2. Aniž byste měnili rozpětí na kompasu, umístěte bod kompasu na bod B a vykružte stejný oblouk, který se protne s prvním obloukem.
3. Označ průsečík jako třetí vrchol rovnostranného trojúhelníku.

Podívej se na plné kružnice při práci.

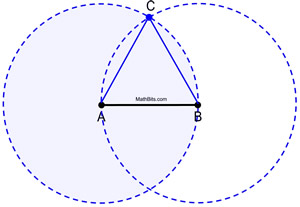Důkaz konstrukce: Kružnice A je kongruentní s kružnicí B, protože každá z nich byla vytvořena pomocí stejné délky poloměru AB. Protože AB a AC jsou délky poloměrů kružnice A, jsou si navzájem rovny. Podobně AB a BC jsou délky poloměrů kružnice B a jsou si navzájem rovny. Proto platí AB = AC = BC podle substituce (neboli tranzitivní vlastnosti). Protože shodné úsečky mají stejné délky, a ΔABC je rovnostranný (má tři shodné strany).

Úkony:
1. Umístěte bod kružítka na papír a nakreslete kružnici. (Toto rozpětí kružítka si nechte!)
2. Umístěte bod označený A kamkoli na obvod kružnice, aby sloužil jako výchozí bod.
3. Aniž byste měnili rozpětí na kružítku, umístěte bod kružítka na bod A a nakreslete malý oblouk protínající obvod kružnice.
4. Aniž byste měnili rozpětí na kružítku, přesuňte bod kružítka na průsečík předchozího oblouku a obvodu a nakreslete další malý oblouk na obvodu kružnice.
5. Aniž byste měnili rozpětí na kružítku, přesuňte bod kružítka na průsečík předchozího oblouku a obvodu a nakreslete další malý oblouk na obvodu kružnice. Tento postup „kroužení“ po kružnici opakujte, dokud se nevrátíte do bodu A.
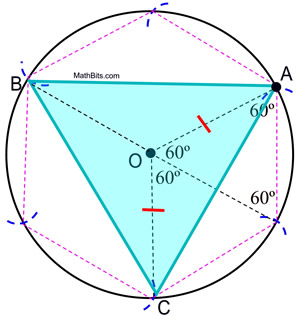
6. Počínaje bodem A spojte každý další oblouk na kružnici tak, aby vznikl rovnostranný trojúhelník.

Další informace týkající se důkazu této konstrukce najdete v důkazu vepsaného pravidelného šestiúhelníku.

Důkaz konstrukce: Důkaz konstrukce vepsaného pravidelného šestiúhelníku ukazuje, že středové úhly pravidelného šestiúhelníku obsahují 60º. Středové úhly trojúhelníku vepsaného do této kružnice obsahují 120º. Protože ΔAOC je rovnoramenný (OA a OC jsou délky poloměrů), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA podle SAS. Podle CPCTC ∠OCB ∠OCA a m∠OCB = 30º substitucí a m∠BCA = 60º. Podobným způsobem máme m∠ACB = m∠CBA = m∠BAC = 60º a rovnostranný ΔABC.

KROKY:
1. Umístěte bod kružítka na papír a narýsujte kružnici O. (Toto rozpětí kružítka zachovejte!)
2. Pomocí pravítka narýsujte průměr kružnice a označte koncové body P a B.
3. Aniž byste měnili rozpětí na kružítku, umístěte bod kružítka na P a narýsujte plnou kružnici.
4. Průsečíky obou obvodů kružnice označte A a C.
5. Kružítko umístěte na papír a narýsujte plnou kružnici. Narýsuj úsečky z A do B, z B do C a z C do A tak, aby vznikl rovnostranný trojúhelník.

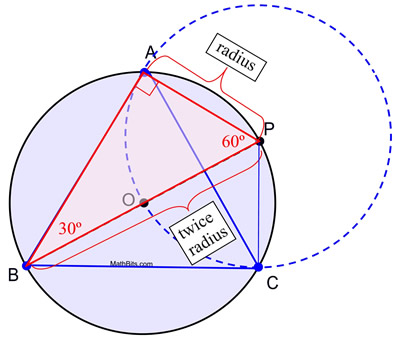
Důkaz konstrukce: Tato konstrukce využívá skutečnosti, že úhel vepsaný do půlkruhu je pravý úhel a že v trojúhelníku 30º-60º-90º je délka kratší odvěsny rovna polovině délky přepony. V této konstrukci jsou kružnice O a kružnice P shodné, protože mají stejnou délku poloměru. AP je délka poloměru kružnice P a poloměry AP = OP. OP je také délka poloměru kružnice O (spolu s OB) a průměr BP = BO + OP = 2 OP. Substitucí získáme BP = 2 AP, čímž vytvoříme podmínky nutné pro m∠ABP = 30º. Z toho vyplývá, že m∠APB = 60º. Podobným argumentem lze zjistit, že pro ΔPBC platí m∠PBC = 30º a m∠BPC = 60º, takže ΔPBC ΔPBA podle ASA (se společnou stranou z B do P).
Nyní , protože jsou to odpovídající strany dvou shodných trojúhelníků, takže ΔABC je rovnoramenný. ∠BAC ∠BCA, protože základní úhly rovnoramenného trojúhelníku jsou shodné.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º podle postulátu sčítání úhlů a substituce. m∠BAC + m∠BCA + m∠ABC = 180º, protože součet úhlových měr v trojúhelníku je 180º. Protože m∠BAC + m∠BAC + 60º = 180º substitucí víme, že 2m∠BAC = 120º a m∠BAC = 60º. Z toho vyplývá, že m∠BCA je substitucí také rovno 60º, takže ΔABC je rovnostranný.

.