Jaká je propustnost buněčné membrány?
Režim čtení
Jednou z charakteristických vlastností všech živých organismů je, že obsahují charakteristickou směs iontů a malých molekul. Toto složení se liší nejen od okolního prostředí, ale může se lišit i uvnitř buňky. Například koncentrace vodíkových iontů v některých buněčných kompartmentech může být 104krát vyšší než v jiných (mitochondrie dosahují pH až 8; lysozomy s pH až 4, BNID 107521, 106074). Poměr koncentrací iontů Ca2+ v kompartmentech extra- a intracelulární tekutiny může být opět 104násobný (BNID 104083). Tento koncentrační rozdíl je tak velký, že transport iontu Ca2+ přes membránu, z intra- do extracelulárního kompartmentu, vyžaduje energii více než jednoho protonu nebo sodného iontu proudícího po gradientu proton-motivační síly. Aby si to čtenář uvědomil, měl by si vzpomenout na pravidlo z našeho seznamu triků, že k vytvoření řádově většího rozdílu potenciálů je třeba 6 kJ/mol (≈2 kBT). Této energie lze dosáhnout například transportem jednoho elektrického náboje přes rozdíl potenciálů 60 mV. K dosažení čtyřřádového poměru koncentrací by pak bylo zapotřebí, aby náboj urazil asi 240 mV elektronové hybné síly (ve skutečnosti ještě více díky dvojnásobnému náboji vápenatého iontu). To je velmi blízko průraznému napětí membrány, jak je popsáno ve vinětě na téma „Jaký je rozdíl elektrických potenciálů přes membrány?“. Vysokého koncentračního poměru Ca2+ se totiž obvykle dosahuje spojením s transportem tří sodíkových iontů nebo hydrolýzou ATP, což pomáhá dosáhnout požadovaného hustotního rozdílu, aniž by se membrána nebezpečně napájela.
Druhý termodynamický zákon nás učí, že obecně platí, že přítomnost koncentračních gradientů bude nakonec vyčerpána procesy transportu hmoty, které systémy neustále vedou do stavu rovnováhy. Nicméně ačkoli nám druhý termodynamický zákon říká povahu konečného stavu systému (např. rovnoměrné koncentrace), neříká nám, jak dlouho bude trvat, než tohoto stavu dosáhneme. Membrány se vyvinuly tak, že tvoří velmi účinnou bariéru pro samovolný přenos mnoha iontových a molekulárních druhů. Abychom mohli odhadnout časové měřítko pro vyrovnání koncentrací, potřebujeme znát rychlosti přenosu hmoty, které závisí na klíčových materiálových vlastnostech, jako jsou difuzní konstanty a propustnosti.
Mimořádně úspěšnou třídou „zákonů“, které popisují chování systémů, u nichž došlo k určité malé odchylce od rovnováhy, jsou lineární transportní zákony. Tyto zákony předpokládají jednoduchý lineární vztah mezi rychlostí transportu nějaké zájmové veličiny a související hnací silou. Pro transport hmoty existuje lineární vztah mezi tokem (tj. počtem molekul, které projdou jednotkovou plochou za jednotku času) a rozdílem koncentrací (který slouží jako příslušná hnací síla). Pro transport přes membrány byly tyto myšlenky kodifikovány v jednoduché rovnici (pro neutrální rozpuštěnou látku) j= – p-(cin-cout), kde j je čistý tok do buňky, cin a cout se vztahují ke koncentracím na vnitřní a vnější straně oblasti ohraničené membránou a p je materiálový parametr známý jako permeabilita. Jednotky p lze odvodit z toho, že tok má jednotky počet/(plocha x čas) a koncentrace má jednotky počet/objem, což znamená, že samotné jednotky p jsou délka/čas. Stejně jako mnoho jiných transportních veličin (např. elektrická vodivost materiálů, která přesahuje 30 řádů) má propustnost velmi velký dynamický rozsah, jak je znázorněno na obrázku 1. Jak je vidět na obrázku, lipidové dvojvrstvy mají téměř 1010násobný rozsah propustnosti.
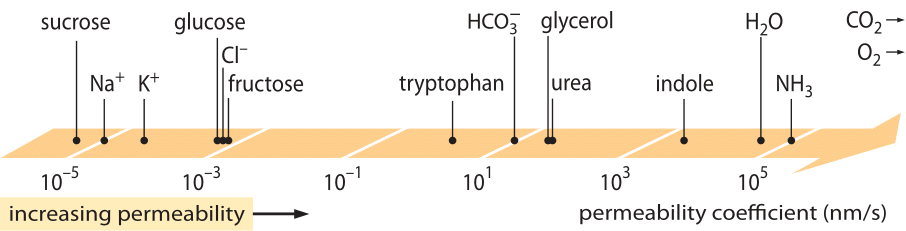
Obrázek 1: Široký rozsah propustnosti membrán různých sloučenin v buňce. Membrány jsou propustnější pro nenabité sloučeniny a nejméně propustné pro nabité ionty. Všimněte si, že existence iontových kanálů způsobí, že zdánlivá propustnost při jejich otevření bude o několik řádů vyšší. Jednotky jsou zvoleny jako nm/s a několik nm je charakteristická šířka membrány. Obrázek převzat z R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. Hodnota pro glukózu je menší než u Robertsona na základě několika zdrojů, například BNID 110830, 110807. Další zdroje údajů:
Jaké fyzikálně-chemické parametry určují umístění sloučeniny na této stupnici propustnosti? Jedním z pravidel je, že malé molekuly mají vyšší propustnost než větší molekuly. Dalším pravidlem je, že neutrální sloučeniny mohou procházet membránou o mnoho řádů rychleji než podobně nabité sloučeniny. Mezi nabitými sloučeninami mají záporné (aniontové) sloučeniny obvykle mnohem vyšší propustnost než kladné (kationtové) sloučeniny. Takzvané Overtonovo pravidlo říká, že propustnost membrány roste s hydrofobností, přičemž hydrofobnost je tendence sloučeniny dávat přednost nepolárnímu rozpouštědlu před polárním (vodným) rozpouštědlem. Overtonovo pravidlo předpovídá, že nabité molekuly (nehydrofobní), jako jsou ionty, budou mít tendenci mít nízkou propustnost, protože jim vzniká energetická škoda spojená s průnikem membránou, zatímco rozpuštěné plyny, jako jsou O2 a CO2, které jsou hydrofobní (protože jsou nenabité a symetrické), budou mít vysokou propustnost. Propustnost lipidových dvouvrstvých membrán pro CO2 skutečně poskytuje hodnoty, které jsou 0,01-1 cm/s (ano, měření propustnosti mají mezi různými laboratořemi velmi vysokou nejistotu, BNID 110004, 110617, 102624), vyšší než všechny ostatní hodnoty uvedené na obrázku 1. Tato hodnota ukazuje, že bariéra vytvořená buněčnou membránou je ve skutečnosti menší překážkou než bariéra způsobená nevětranou vrstvou vody pohlcující buněčnou membránu zvenčí. Takový závěr lze odvodit z rovnice pro koeficient propustnosti překážky, která je dána vztahem p=K x D/l, kde l je šířka, D difuzní koeficient a K rozdělovací koeficient mezi médiem a materiálem překážky. Tento model je také známý jako „rozpustnostně-difuzní“ model propustnosti, kde se označují efekty K a D, což jsou dva stupně ovlivňující propustnost. Pro nezavzdušněnou vrstvu vody je K=1, protože je velmi podobná médiu, ale pro membránu je hodnota pro všechny materiály kromě těch nejhydrofobnějších obvykle o několik řádů menší než 1. Tato závislost na K je podstatou výše zmíněného Overtonova pravidla. Vysoká propustnost pro CO2 také naznačuje, že kanály, jako jsou akvaporiny, které měly sloužit k transportu plynu do buňky, nejsou nutné, protože membrána je dostatečně propustná. Abychom zjistili, jak vlastnosti membrány ovlivňují chemické složení metabolitů, přejdeme k výpočtu doby úniku pro různé sloučeniny
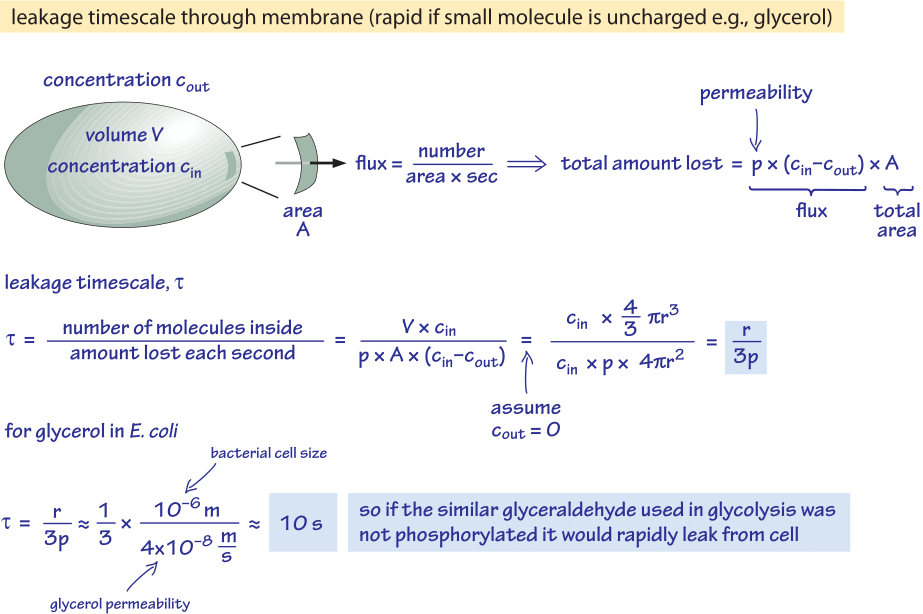
Obr. 2: Výpočet časového průběhu pasivní difúze nefosforylované molekuly glukózy z bakteriální buňky pomocí Back of the envelope. Funkční důsledky jsou pak uvažovány pro rychle rostoucí buňku, kde je tento efekt zanedbatelný, a pro buňky ve stacionárním stavu, kde může způsobit znatelný únik zdrojů.
Uvažujeme například glycerol. Analýza uvedená na obrázku 2 poskytuje odhad doby jeho úniku z buňky, pokud molekula není fosforylována nebo jinak přeměněna na hydrofilnější formu. Propustnost buněčné membrány pro glycerol je p≈10-100 nm/s (BNID 110824), jak lze vyčíst z obrázku 1. Časovou škálu, za kterou molekula glycerolu uvnitř buňky unikne zpět do okolního prostředí, za předpokladu, že do buňky neproudí žádný zpětný tok (cout=0), lze přibližně odhadnout tak, že se zjistí, že odtok z buňky je p-A-cin, kde A je plocha povrchu buňky. Časová stupnice se zjistí tak, že se vezme celkové množství v buňce, V-cin (kde V je objem buňky nebo přesněji objem vody v buňce), a vydělí se tímto tokem, což pro bakteriální buňku (r≈1 μm) znamená časovou stupnici:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Jedná se o hrubý odhad, protože jsme nezohlednili klesající koncentraci cin s časem, která dá korekční faktor 1/ln(2), tj. méně než 2násobný nárůst. Z těchto odhadů vyplývá, že pokud by glykolytické meziprodukty glyceraldehyd nebo dihydroxyaceton, které jsou velmi podobné glycerolu, nebyly fosforylovány, což by vedlo k přidání náboje, ztrácely by se do prostředí difuzí přes buněčnou membránu. V laboratorních médiích, kde je zdroj uhlíku dodáván v hojném množství, to není zásadní problém, ale v přirozeném prostředí, kde buňky často čekají ve stacionární fázi na šťastný puls živin (E. coli po vyloučení z těla projde měsíci bez růstu, než najde nového hostitele), může buňka omezit své ztráty tím, že se ujistí, že metabolické meziprodukty jsou označeny nábojem, který jim zabrání znovu překonat bariéru, kterou představuje lipidová dvojvrstva.





.