SPSS統計学でポアソン回帰分析を行う方法｜Laerd Statistics

はじめに

ポアソン回帰は、一つ以上の独立変数から「カウントデータ」からなる従属変数を予測するために使用されるものです。我々が予測したい変数は、従属変数（または応答、結果、目標、基準変数）と呼ばれます。従属変数の値を予測するために我々が使用している変数は，独立変数（または予測変数，説明変数，リグレッサ変数）と呼ばれる．ポアソン回帰が使用できるいくつかの例を以下に説明します：

例1：性別（女子と男子）、人種（白人、黒人、ヒスパニック、アジア/太平洋諸島人、アメリカン・インディアン/アラスカ・ネイティブ）、言語（英語が第一言語、英語が第一言語ではない）、障害状況（障害者と非障害者）などの予測変数に基づいてアメリカのワシントン州の学校から出場停止の生徒数を調査するのにポアソン回帰が使用できます。ここで、「停学回数」が従属変数で、「性別」、「人種」、「言語」、「障害の有無」はすべて名目上の独立変数です。
例2：オーストラリアの人々が、仕事の状況（雇用、無職）、年収（オーストラリアドル）、年齢（年）、性別（男性、女性）、国の失業レベル（%失業中）などの予測変数に基づいて5年間にクレジットカード返済を怠る回数を検討するのにポワソン回帰が使用できると思います。ここで、「クレジットカードの返済不履行回数」を従属変数とし、「雇用形態」と「性別」を名目独立変数、「年収」「年齢」「国内の失業水準」を連続独立変数としている。
例3：Accident & Emergency (A&E) departmentで、A&Eへの到着方法（救急車かセルフチェックイン）、トリアージ時の傷害の評価された重さ（軽度、中度、高度）、時間帯、曜日といった予測因子に基づいて、列であなたの前の人の数を調査するのにポワソン回帰を使用することができます。ここで、「行列の前の人の数」は従属変数であり、「到着の形態」は名目独立変数、「評価された傷害の重症度」は順序独立変数、「時間帯」及び「曜日」は連続独立変数である。
例4: MBAプログラムで1等賞を授与された学生の数を、彼らが選んだ選択コースの種類（主に数値、主に質的、数値と質的の混合）およびプログラム入学時のGPAなどの予測変数に基づいて調査するためにポアソン回帰を使用することができるでしょう。ここで、「1級学生の数」は従属変数であり、「選択科目」は名義独立変数、「GPA」は連続独立変数です。

ポアソン回帰を実施すると、どの独立変数（もしあれば）が従属変数に統計的に有意な影響を持つかを決定することができるようになります。カテゴリ独立変数では、あるグループ (例: ジェットコースターに乗る「子供」の死亡) と別のグループ (例: ジェットコースターに乗る「大人」の死亡) のカウントの増加または減少の割合を決定することができるようになります。連続した独立変数については、その変数の1単位の増加または減少が、従属変数のカウントのパーセントの増加または減少とどのように関連しているかを解釈できるようになります（たとえば、給与の1,000ドルの減少 – 独立変数 – オーストラリアの人々がクレジットカードの返済を不履行にする回数のパーセントの変化 – 依存変数）

この「クイックスタート」ガイドは、SPSS統計を使ってポアソン回帰を実行する方法、およびこのテストから結果を解釈して報告することをお見せするものです。しかし、この手順を紹介する前に、ポアソン回帰が有効な結果を与えるために、あなたのデータが満たさなければならないさまざまな仮定を理解する必要があります。

Note: We currently have no premium version of this guide in the subscription part of our website.

SPSS Statistics

Assumptions

When you choose to analyze your data using Poisson regression, the process part of involves checking to ensure that you want to analyze the data actually can be analyzed using Poisson regression.このような仮説を立てるには、次のように説明することができます。これは、ポアソン回帰が有効な結果を得るために必要な5つの仮定をデータが「パス」している場合のみ、ポアソン回帰を使用することが適切であるため、行う必要があります。実際には、ポアソン回帰を実行するとき、これらの5つの仮定をチェックすることが、時間の大部分を占めます。しかし、これらの仮定の1つ以上に違反する（＝満たさない）データも珍しくないので、これを行うことは必須です。しかし、仮にこれらの仮定を満たさないデータであっても、それを克服するための解決策がある場合が多いのです。まず、これらの5つの仮定を見てみましょう。

仮定1：あなたの従属変数はカウントデータから構成されている。カウント・データは、他のよく知られたタイプの回帰で測定されるデータとは異なります（例えば、線形回帰や重回帰は、「連続」スケールで測定される従属変数を必要とし、二項ロジスティック回帰は「二項」スケールで測定される従属変数を必要とし、順序回帰は「順序」スケールで測定される従属変数を、多重項ロジスティック回帰は「名目」スケールで測定される従属変数を必要とします). 一方，カウント変数は，ゼロ以上でなければならない整数のデータを必要とする．簡単に言うと、「整数」とは「全部」の数（例えば、0、1、5、8、354、888、23400など）だと考えてください。また、カウントデータは「正」でなければならないので（つまり「非負」の整数値で構成される）、「負」の値で構成することはできない（例えば、-1、-5、-8、-354、-888、-23400といった値はカウントデータとはみなされない）。さらに、ポアソン回帰は平均カウントが小さな値（例えば、10未満）である場合にのみ実行するように提案されることがあります。カウントの数が多い場合は、別のタイプの回帰がより適切かもしれません（例：重回帰、ガンマ回帰など）。
カウント変数の例としては、ヨーロッパの空港で3時間以上遅れたフライトの数、アメリカのワシントン州の学校で停学になった生徒の数、オーストラリアの人々が5年間にクレジットカードの返済を滞らせた回数、などがあります。病院の事故＜411＞救急（A&E）部門の行列で自分の前にいる人の数、MBAプログラムで1級マークを授与される学生の数（通常5人未満）、米国でジェットコースターの事故で死亡した人の数。
前提2：1つ以上の独立変数があり、それらは連続、順序、または名義/二分尺度で測定されることができます。順序変数と名目/二項変数は、大まかに分類するとカテゴリー変数に分類されます。
連続変数の例としては、修正時間（時間で測定）、知能（IQスコアを使用して測定）、試験成績（0から100で測定）、体重（kgで測定）などがあります。順序変数の例には、カテゴリのランク付けの他の方法（例えば、顧客が製品をどの程度好きかを説明する、「あまり好きでない」から「とても好きである」までの3点スケール）のうち、リカート項目（例えば、「強くそう思う」から「強くそう思わない」までの7点スケール）などが含まれる。名義変数の例としては、性別（たとえば、2つのグループ – 男性と女性 – だから、二項変数としても知られています）、民族（たとえば、3つのグループ：白人、アフリカ系アメリカ人、ヒスパニック）、職業（たとえば、5つのグループ：外科医、医者、看護師、歯科医、セラピスト）などが挙げられます。順序変数と名義・二項変数は、カテゴリ変数に大別されることを忘れないでください。変数については、こちらの記事で詳しく解説しています。
前提3：オブザベーションの独立性があること。これは、各オブザベーションが他のオブザベーションから独立していることを意味します。つまり、あるオブザベーションは、他のオブザベーションに関するいかなる情報も提供することはできません。これは非常に重要な仮定です。独立したオブザベーションの欠如は、ほとんどの場合、研究デザインの問題です。オブザベーションの独立性の可能性を検定する1つの方法は、標準モデル・ベースの誤差をロバスト誤差と比較して、大きな差があるかどうかを決定することです。
仮定 #4: カウントの分布（モデルの条件付き）は、ポアソン分布に従います。この帰結として、観測されたカウントと期待されるカウントは等しくなるはずである（現実には、非常に似ているだけである）。本質的に、これはモデルが観測されたカウントをよく予測することを言っています。これはいろいろな方法でテストできますが、1つの方法は期待カウントを計算し、それを観測カウントとプロットし、それらが似ているかどうかを見ることです。
仮定5：モデルの平均と分散は同一である。これは仮定4の結果で、ポアソン分布が存在することになります。ポアソン分布の場合、分散は平均と同じ値を持ちます。この仮定を満たせば、等分散となります。しかし、多くの場合、この仮定は当てはまらず、データは過小または過大に分散しており、過大分散の方がより一般的な問題です。過分散を評価する方法はいろいろあります。

SPSS Statistics を使用して、仮定 #3、#4、#5 をチェックすることができます。仮定#1、#2を先に確認し、仮定#3、#4、#5に移るのがよい。これらの仮定に対する統計的検定を正しく行わないと、ポアソン回帰を行ったときに得られる結果が妥当でない可能性があることを覚えておいてください。

また、ポアソン回帰を行うときに非常によくある仮定#5にデータが違反している場合、まず「見かけのポアソン過剰分散」があるかどうかを確認する必要があります。見かけのポアソン過剰分散とは、データが過剰に分散しているように見えるような、正しいモデルの指定をしていない場合です。したがって、ポアソンモデルが最初に等分散の仮定に違反した場合、まずポアソンモデルに多くの調整を加え、実際に過分散であることを確認する必要があります。そのためには、モデルやデータに対して6つのチェックをする必要があります。 (a) ポアソン・モデルはすべての重要な予測変数を含んでいるか? (b) データは外れ値を含んでいるか? (c) ポアソン回帰はすべての関連する相互作用項を含んでいるか?(f) Missing at random (MAR) でない欠損値を持っていますか？

手順のセクションでは、仮定が違反されていないと仮定してポアソン回帰を実行する SPSS Statistics の手順を説明します。まず、このガイドで使用される例を紹介します。

SPSS Statistics

例 & SPSS Statisticsでの設定

小さな大学の研究部長は、学者の経験と彼らが研究を遂行するために利用できる時間が、彼らが作り出す出版物の数に影響を与えるかどうかを評価したいと思います。そこで、大学から無作為に抽出した21名の研究者に調査への参加を依頼した。 10人は経験豊富な研究者、11人は最近の研究者である。過去12ヶ月間に彼らが研究に費やした時間数と、彼らが生み出した査読付き出版物の数が記録される。

SPSS Statisticsでこの研究デザインを設定するために、3つの変数を作成した。 (1) no_of_publications、これは過去12ヶ月間に学術誌に発表した論文の数である。(2) experience_of_academic、これはその学術者が経験豊富であるか（すなわち、10年以上学術界で働いており、したがって「経験のある学術者」として分類される）または最近学術者となった（すなわち, (3) no_of_weekly_hours（研究者が毎週研究に従事することができる時間数）。

SPSS Statistics

SPSS Statisticsでのテスト手順

以下の13ステップは、前のセクション「前提条件」の5つの前提条件のいずれにも違反していない場合に、SPSS Statisticsでポアソン回帰を使用してデータを分析する方法を示しています。この13のステップの最後に、ポアソン回帰の結果を解釈する方法を紹介します。

解析 > 一般化線形モデル > 一般化線形モデル… をクリックします。 8248>
Published with written permission from SPSS Statistics, IBM Corporation.

You will be presented with the Generalized Linear Models dialogue box below:

Published with written permission from SPSS Statistics, IBM Corporation.メインメニューで、以下のように、”一般化線形モデル “の対話ボックスを表示される。
Select Poisson loglinear in the area, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.より。

注意：ポアソン回帰を実行するために領域でポアソンログリニアを選択することが標準ですが、領域でカスタムを選択し、分布：、リンク関数：および-パラメータ-オプションを使用して実行したいポアソンモデルの種類を指定して、カスタムポアソン回帰を実行することもできます:
タブを選択してください。次のダイアログボックスが表示されます：

Published with written permission from SPSS Statistics, IBM Corporation.
従属変数 no_of_publications を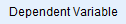エリアの Dependent variable: ボックスにボタンを使用して、以下のように転送します:

Published with written permission from SPSS Statistics, IBM Corporation.
Select the tab. 以下のダイアログボックスが表示されます：

Published with written permission from SPSS Statistics, IBM Corporation.
以下に示すように、ボタンを使用して、カテゴリ独立変数、experience_of_academic を Factors: ボックスに、連続独立変数 no_of_weekly_hours を Covariates: ボックスに転送してください。

Published with written permission from SPSS Statistics, IBM Corporation.

注1：順序独立変数がある場合、これらをカテゴリーとして扱い、Factors: ボックスに入力するか、連続として扱い、Covariates: ボックスに入力するかを決める必要があります。

注意2: 連続の独立変数をCovariates: ボックスに入力するのが一般的ですが、代わりに序数の独立変数を入力することも可能です。

注意3: ボタンをクリックすると、次のダイアログ・ボックスが表示されます：

「要因のカテゴリ順」領域では、昇順、降順、データ順の使用オプションから選ぶことができます。 SPSS Statistics は自動的にカテゴリ変数をダミー変数に変えるので、これらは便利です。ダミー変数に精通していない限り、これはカテゴリ変数の各グループのポアソン回帰からの出力を解釈することを少し難しくすることができます。
タブを選択します。次のダイアログボックスが表示されます：

Published with written permission from SPSS Statistics, IBM Corporation.
-Build Term(s)- エリアではデフォルトのを維持し、Factors and Covariates: ボックスからボタンを使用して、カテゴリおよび連続独立変数 experience_of_academic と no_of_weekly_hours を Model: ボックスに転送すると、下図のようになります：

Published with written permission from SPSS Statistics, IBM Corporation.の記事より。

注1：ポアソンモデルを構築するのはダイアログボックスである。特に、主効果（オプション）、独立変数間の交互作用（オプション）があるかどうかを決定するのです。独立変数間の交互作用があると思われる場合、モデルにこれらを含めることは、モデルの予測を改善するだけでなく、前述の仮定セクションで強調したように、過分散の問題を回避するためにも重要です。
ここでは、単一の主効果（独立変数experience_of_academicとno_of_weekly_hoursの間）を持つ非常に単純なモデルの例を提供しますが、、、を使用してより複雑なモデルを簡単に入力することができます。

Note 2: また、-Build Nested Term-領域のTerm: ボックスに追加することにより、モデルに入れ子の項を作成することができます。このモデルではネストされた効果はありませんが、モデル内にネストされた項がある可能性は多くあります。
タブを選択します。次のダイアログボックスが表示されます：

Published with written permission from SPSS Statistics, IBM Corporation.
デフォルトのオプションが選択されたままにします。
注: 「パラメータ推定」領域内で選択できるオプションには、異なるものを選択する機能が多数あります。 (a)スケールパラメーター法 (すなわち、スケールパラメーター法: ボックスのの代わりに ) は、過分散の問題に対処するために考慮されるかもしれません。(b) 共分散行列 (すなわち、-共分散行列-エリアのモデルベース推定量ではなくロバスト推定量) は、過分散の問題を扱うための別のオプション (とりわけ、他のもの) が提示されます。
タブを選択します。次のダイアログボックスが表示されます：

Published with written permission from SPSS Statistics, IBM Corporation.
Select Include exponential parameter estimates in the area, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.Published as aptitude.

注1：エリアでは、サンプルサイズとこれが統計的有意性検定の精度に与える影響などの要因に基づいて、Waldと尤度比のいずれかを選択することができます。
エリアでは、ラグランジュ乗数検定は、ポアソンモデルがデータに適切かどうかを判断するのにも役立ちます（ただし、これはポアソン回帰手順を使用して実行できません）。

注 2: およびタブから他のオプションを幅広く選択することも可能です。これらは、カテゴリー変数のグループ間の違いを調べるとき、また、前述の「仮定」のセクションで説明したように、ポアソン回帰の仮定をテストするときに重要なオプションが含まれています。これは、出力を生成します。

SPSS Statistics

Interpreting and Reporting the Output of Poisson Regression Analysis

SPSS Statistics will generate quite a table of output for a Poisson regression analysis.これは、ポアソン回帰分析の出力の多くのテーブルが生成されます。このセクションでは、仮定が違反されていないと仮定して、ポアソン回帰手順から結果を理解するために必要な8つの主要なテーブルを紹介します。

モデルおよび変数情報

出力内の最初のテーブルは、モデル情報テーブル（以下に示すように）です。これは、従属変数が「論文数」、確率分布が「ポアソン」、リンク関数が自然対数（つまり「Log」）であることを確認するものです。自分のデータでポアソン回帰を実行する場合、従属変数の名前は異なりますが、確率分布とリンク関数は同じになります。