生命科学から3つの例を説明する。物理学から1つ、遺伝学に関連するもの、そしてマウス実験から1つ。 これらは非常に異なっていますが、結局は同じ統計的手法、つまり線形モデルのあてはめを使います。
Motivating Examples
Falling objects
16 世紀のガリレオが、落下物体の速度を記述しようとしていると想像してください。 助手がピサの塔に登って球を落とし、他の数人の助手が異なる時刻にその位置を記録します。
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##meters助手がガリレオにデータを渡すと、彼はこれを見ます:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")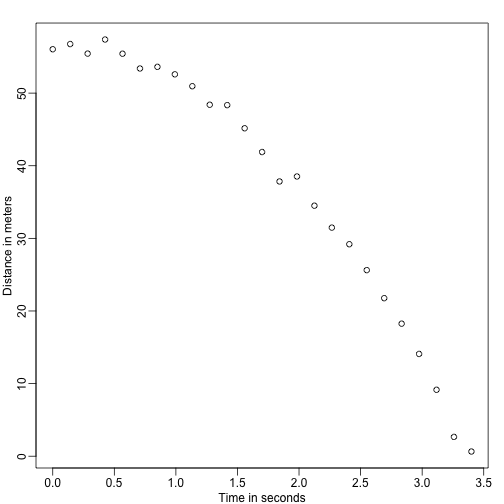
彼は正確な方程式を知っていませんが、上のグラフを見て、位置は放物線を描くはずだと推理します。 そこで、彼はデータを次のようにモデル化します:
位置を表し、時間を表し、測定誤差を考慮する。 これは、予測変数または共変量と呼ばれる既知の量 (th s) と未知のパラメータ (the s) の線形結合であるため、線形モデルです。
Father & Son heights
さて、あなたが 19 世紀のフランシス ホールトンで、父親と息子から一対の身長データを収集したとします。 あなたは身長が遺伝するのではないかと疑っています。
library(UsingR)x=father.son$fheighty=father.son$sheight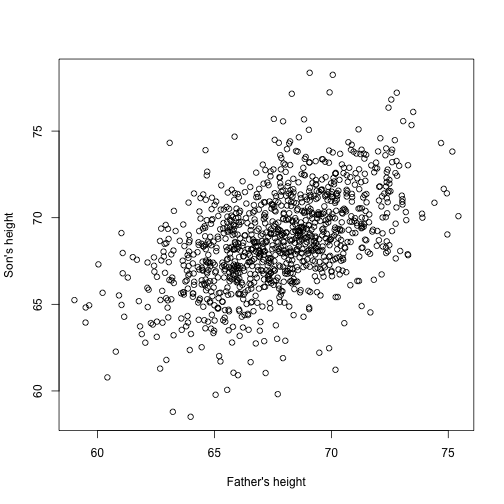
息子の身長は父親の身長と直線的に増加するように見える。 この場合、データを記述するモデルは次のようになります:
これも線形モデルで、-番目のペアの父親と息子の身長をそれぞれandとし、余分な変動性を考慮する項を設けます。 ここでは父親の身長を予測変数と考え、固定的(ランダムではない)なので小文字を使っています。 測定誤差だけでは、.NETで見られるすべての変動を説明することはできません。 3279>
Random samples from multiple populations
ここで、高脂肪とコントロール(chow)の2種類の餌を与えたマウスの体重データを読み込んでみます。 それぞれ12匹のマウスを無作為にサンプリングしています。 食餌が体重に影響を与えるかどうかを判断したいのです。 以下はそのデータです:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")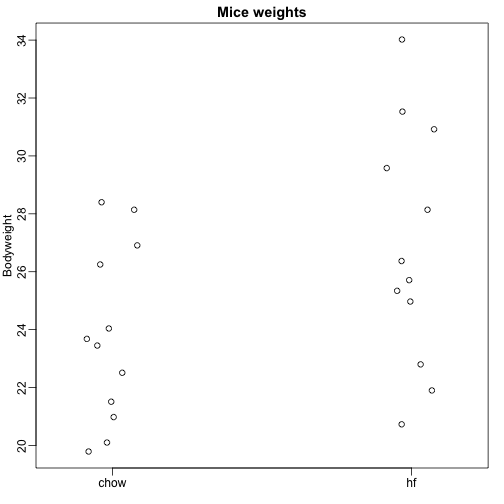
我々は集団間の平均体重の差を推定したいのです。 標本平均の差から、t検定と信頼区間を用いてこれを行う方法を示しました。
平均体重、平均値の差、マウスが高脂肪食になったとき、低脂肪食になったとき、同じ集団のマウス間の差を説明する線形モデルを使っても同じ結果を得ることができます。 上記の例をすべて包含する一般的なモデルは次のようになります。
Note that we have a general number of predictors .
Estimating parameters
For the models above to be useful we have to estimate the unknown s. 最初の例では、未知のパラメータを持つことができない物理プロセスを記述したい。 2つ目の例では、父親の身長が息子の身長に平均してどの程度影響するかを推定することで、遺伝をより理解することができます。 最後の例では、実際に差があるかどうかを判断したい。もし.
科学における標準的なアプローチは、データに対する適合モデルの距離を最小化する値を見つけることである。 以下は最小二乗(LS)式と呼ばれ、この章ではよく目にする。
最小値を見つけたら、その値を最小二乗推定値(LSE)と呼び、それを.と表記することにする。 その推定値で最小二乗方程式を評価したときに得られる量を残差平方和(RSS)と呼びます。 これらの量はすべて , に依存するので,これらは確率変数である.
落下物の例
高校の物理の先生のおかげで、落下物の軌道の方程式は
で、それぞれ開始時の高さと速度であることを知っています。 この式に従って、ピサの塔からボールを落としたときの観測結果をシミュレートするために、測定誤差を加えたのが、上でシミュレートしたデータです n 。
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)ここで、実線が真の軌道を表すと、データはどのように見えるでしょうか:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)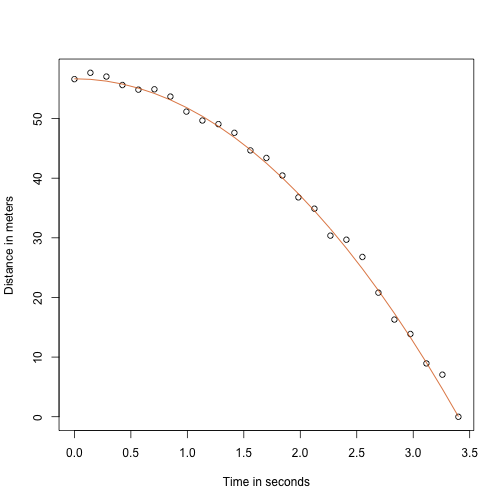
しかし、我々はGalileoを気取っていたので、モデル内のパラメータはわかりません。
どうやってLSEを見つけるか。
The lm function
R では、単に lm function を使ってこのモデルをフィットさせることができます。 この関数については後で詳しく説明しますが、ここではそのプレビューを示します。
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17これは LSE、および標準誤差と p 値を教えてくれます。
このセクションで行うことの一部は、この関数の背後にある数学について説明します。
最小二乗法による推定値 (LSE)
任意のベクトルについて RSS を計算する関数を書いてみましょう。 以下は、他の 2 つを固定した場合の関数としての RSS のプロットです:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)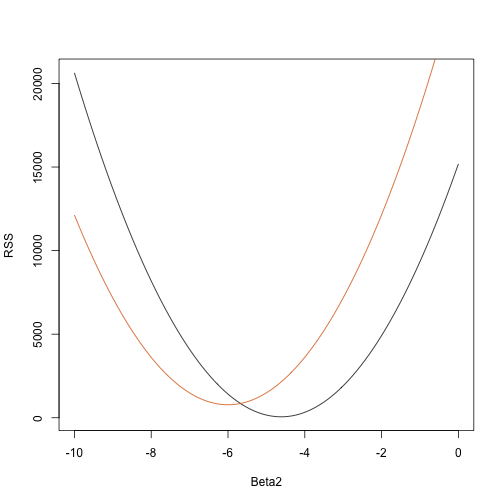
ここで試行錯誤してもうまくいかないでしょう。 代わりに微積分を使います。偏導関数をとり、それを0にして解きます。 もちろん、多くのパラメーターがある場合、これらの方程式はかなり複雑になる可能性があります。
More on Galton (Advanced)
親子データを研究していたとき、Galton は探索的分析を使って興味深い発見をした。 ガルトンが作成した上のプロットでは、3つのケースを持つペアが楕円を形成しているのがわかります。 3279>
私たちは、数学を使って、もし固定(となる条件)にしておけば、平均: と標準偏差: を持つ正規分布になることを示す方法を説明しました。 との間に相関があることに注意してください。これは、もし固定すれば、実際には線形モデルに従うことを意味します。 この単純な線形モデルのパラメータは、 , と .
で表すことができる。