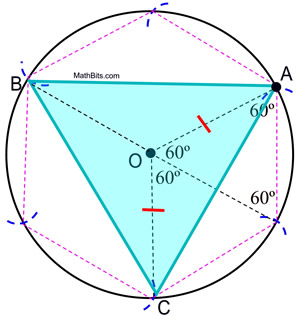
この作図の証明に関わる詳細な情報は、内接正六角形の証明を参照してください。 内接正六角形の証明は、正六角形の中心角が60°を含むことを示す。 この円に内接する三角形の中心角は120ºを含む。 ΔAOCは二等辺三角形(OAとOCは半径の長さ)なので、m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC

ΔCOB

ΔBOA by SASとなる。 CPCTCにより、∠OCB<5251>∠OCAとなり、代入によりm∠OCB=30º、m∠BCA=60ºとなる。 同様に、m∠ACB=∠CBA=m∠BAC=60゜となり、正三角形ΔABC.
方法3:
|
与えられたもの:紙1枚
構成:円に内接する正三角形.円形に内接する正三角形を構成する。
|
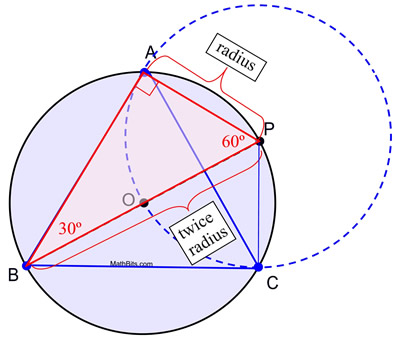
この方法は特殊な直角三角形30°-60°-90°の知識を利用するものである。
|
steps:
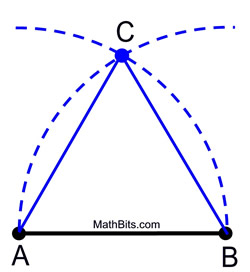
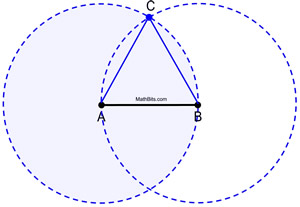
1. コンパスの点を紙の上に置き、円Oを描く。(このコンパスのスパンを保つ!)
2. 直定規を使って円の直径を描き、端点PとBをラベル付けする。
3. コンパスのスパンを変えずに、Pにコンパスの点を置いて一周描く。
4. 二つの円周の交点をA、Cとラベル付けする。
5. AからB、BからC、CからAへ線を引き、正三角形を作る。
作図を証明する。 半円に内接する角は直角であること、30°-60°-90°の三角形では短足の長さは斜辺の長さの半分であることを利用した作図である。 この作図では、円Oと円Pは半径の長さが同じであるため合同である。 AP は円 P の半径の長さであり、半径 AP = OP である。 OPも円Oの半径長(OBと一緒)であり、直径BP = BO + OP = 2 OPである。 代入するとBP=2APとなり、m∠ABP=30゜に必要な条件が整う。 その結果、m∠APB=60゜となる。 同様の論法でΔPBCについても、m∠PBC=30゜、m∠BPC=60゜となり、ASAによりΔPBC<5251>ΔPBA(BからPまで共有辺)<8617>が成り立つ。ここで、二つの合同な三角形の対応辺なので<511>、ΔABCは2等辺となる。 二等辺三角形の底角は合同なので、∠BAC  ∠BCA となります。
∠BCA となります。
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º 角度加算仮定と代入により、m∠BAC + m∠BCA + m∠ABC = 180º 三角形の角度の和は180°であるため、m∠BAC + m∠BCA = 180º 。 代入によりm∠BAC+m∠BAC+60º=180ºとなるので、2m∠BAC=120º、m∠BAC=60ºとなります。 したがってm∠BCAも代入で60゜になり、ΔABCは正三角形になります。