Introduction
Picture this – あなたは次期iPhoneの価格予測を任されており、過去のデータを提供されています。 これには、四半期ごとの売上、前月比の支出、および Apple の貸借対照表に付随する多数のものなどの特徴があります。 データサイエンティストとして、これはどのような問題に分類されるでしょうか。
製品の売上予測から家庭の電力使用量の推定まで、時系列予測は、データサイエンティストであれば、習得していないにしても、知っていることが期待される中核的なスキルの 1 つです。

まず、ARIMA の概念を理解し、メイン トピックである自動 ARIMA につなげていきます。
目次
- 時系列とは
- 時系列予測の方法
- ARIMAへの導入
- ARIMAの実装ステップ
- なぜAutoARIMAが必要なのか
- 時系列予測の方法
- 自動ARIMAの実装(航空旅客データセット)
- 自動ARIMAはどのようにパラメータを選択するのか
ARIMAへの導入ステップなぜAutoARIMAは必要かAutomaticとは ARIMAとは
時系列とそのテクニック(移動平均、指数平滑化、ARIMAなど)に慣れている方は、4節まで直接読み飛ばしていただいて結構です。
時系列とは
時系列データを扱う技法を学ぶ前に、まず時系列とは何か、他の種類のデータとどう違うのかを理解する必要があります。 以下は、時系列の正式な定義です。「一定の時間間隔で測定された一連のデータポイントである。 これは、特定の値が、1時間ごと、毎日、毎週、10日ごとなど、一定の間隔で記録されていることを意味します。 時系列と異なる点は、時系列の各データポイントが前のデータポイントに依存していることである。 5596>
例 1:
ある会社からローンを組んだ人のデータセットがあるとします (下の表に示すとおり)。 各行が前の行と関連していると思いますか? そうではありません。 ローンを組んだ人は、その人の経済状況やニーズに基づいています(家族の人数など他の要因も考えられますが、ここでは簡単のために収入とローンの種類だけを考えています)。 また、このデータは特定の時間間隔で収集されたものではありません。 5596>

例 2:
別の例を見てみましょう。 1日あたりの大気中のCO2濃度を含むデータセットがあるとします(下のスクリーンショット)。 過去数日間の値を見て、翌日のおおよその CO2 量を予測できるでしょうか。 まあ、もちろんです。 5596>

もう直感的にわかったと思いますが、最初のケースは単純な回帰問題、2番目は時系列問題です。 この時系列の問題は線形回帰でも解けますが、相対的な過去の値との関係が無視されるので、あまり良い方法とは言えません。 それでは、時系列問題を解くためによく使われるテクニックをいくつか見ていきましょう。
時系列予測の方法
時系列予測の方法にはいくつかあり、このセクションではそれらを簡単に説明します。 以下のすべての手法の詳細な説明とpythonコードは、この記事で見ることができます。 7 techniques for time series forecasting (with python codes).
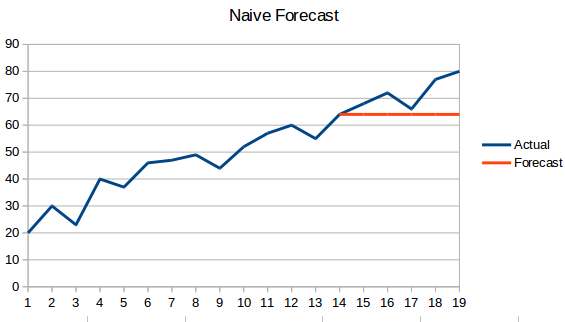
- Naive Approach: この予測手法では、新しいデータポイントの値は、以前のデータポイントと同じになるように予測されます。 すべての新しい値が以前の値を取るので、結果は平らな線になります。
- 単純平均。 次の値は以前のすべての値の平均としてとられる。 単純平均:次の値を過去のすべての値の平均とする。平坦な線にならないので、この予測は「ナイーブ・アプローチ」よりも優れているが、ここでは過去のすべての値が考慮されるので、必ずしも有用ではないかもしれない。 例えば、今日の気温を予測するように言われたら、1ヶ月前の気温ではなく、過去7日間の気温を考慮します。

- 移動平均:これは前の手法の改良版です。 過去のすべてのポイントの平均を取るのではなく、過去の「n」個のポイントの平均を予測値とします。

- 加重移動平均 : 加重移動平均は、過去の「n」個の値に異なる重みをつけた移動平均です。

- 単純指数平滑化:この手法では、遠い過去からの観測値よりも最近の観測値に大きな重みが割り当てられます。

- Holtの線形トレンドモデル:Holtの線形トレンドモデル。 この方法は、データセットの傾向を考慮する。 トレンドというのは,系列の増加または減少の性質を意味する. あるホテルの予約数が毎年増加するとすると、予約数は増加傾向を示していると言える。 この手法の予測関数は、水準とトレンドの関数です。

- Holt Winters Method: このアルゴリズムは、系列のトレンドと季節性の両方を考慮に入れています。 例えば、ホテルの予約数は週末に多く、平日は少なく、毎年増加する。週単位の季節性と増加傾向が存在する。

- ARIMA: ARIMAは時系列モデリングのための非常に人気のある手法である。 これはデータポイント間の相関を記述し、値の差を考慮するものである。 ARIMAを改良したものにSARIMA(または季節性ARIMA)があります。
ARIMA入門
このセクションでは、Auto Arimaを理解するのに役立つARIMAを簡単に紹介することにします。 有馬の詳細な説明、パラメータ(p、q、d)、プロット(ACF PACF)、および実装はこの記事に含まれています。
ARIMA は時系列予測のための非常に一般的な統計手法です。 ARIMAとは、Auto-Regressive Integrated Moving Averagesの略です。 ARIMAモデルは次のような前提で動作します。
- データ系列は定常であり、平均と分散は時間とともに変化しないはずです。 ARIMAは、AR(自己回帰項)、I(差分項)、MA(移動平均項)の3つの要素から構成されています。 AR項とは、次の値を予測するために使われる過去の値のことです。 AR項はarimaのパラメータ’p’で定義されます。 pの値はPACFプロットを使って決定されます。
- MA項は、将来の値を予測するために使われる過去の予測誤差の数を定義するために使われます。 arimaのパラメータqはMA項を表している。 ACFプロットは正しいqの値を識別するために使用されます。
- Order of differencingは、シリーズを定常状態にするために差分操作が実行される回数を指定します。 ADFやKPSSのようなテストは、シリーズが定常であるかどうかを判断し、d値を識別するのに役立ちます。
ARIMA実装のためのステップ
ARIMAモデルを実装する一般的な手順は、 –
- データの読み込みを行う。 モデル構築の最初のステップは、もちろんデータセットの読み込みです
- 前処理を行う。 データセットに応じて、前処理のステップを定義する。 これはタイムスタンプの作成、日付/時間列のd型の変換、系列の一変量化などが含まれる
- 系列を定常化する。 この仮定を満たすために、系列を定常化する必要がある。 これには系列の定常性を確認し、必要な変換を行うことが含まれる
- d値を決定する。 系列を定常化するために、差分演算を行った回数をd値とする
- ACFおよびPACFプロットを作成する。 これはARIMAの実装で最も重要なステップである。 ACF PACFプロットはARIMAモデルの入力パラメータを決定するために使用される
- pとqの値を決定する。 前のステップでプロットからpとqの値を読み取る
- ARIMAモデルをフィットさせる。 処理したデータと前のステップで計算したパラメータ値を使って、ARIMAモデルをあてはめる
- 検証セットで値を予測する。 将来の値を予測する
- RMSEを計算する:モデルのパフォーマンスを確認するために、検証セットの予測値と実際の値を使ってRMSE値を確認する
Why do we need Auto ARIMA? ARIMAを実装する前に、系列を静止させ、上で説明したプロットを使用してpとqの値を決定する必要があります。 Auto ARIMAを使えば、前のセクションで見たステップ3から6を省くことができるので、この作業は本当に簡単です。 以下は、自動ARIMAを実装するための手順です。
- データをロードします。 このステップは同じになります。 ノートブックにデータを読み込む
- Preprocessing data: 入力は一変量でなければならないので、他の列は削除する
- Fit Auto ARIMA: 一変量系列にモデルをフィットさせる
- Predict values on validation set: 検証セットで値を予測する。 検証セットで予測する
- Calculate RMSE: 実際の値に対する予測値を使用してモデルのパフォーマンスをチェックする
ご覧のように、pとq特徴の選択を完全に回避することが出来ました。 なんということでしょう。 5596>
Implementation in Python and R
今回はInternational-Air-Passengerというデータセットを使用します。 このデータセットには、毎月の乗客数(単位:千人)の合計が格納されています。 月と旅客数の2つの列があります。
#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)
output -76.51355764316357
以下は同じ問題に対するRコードです:
# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)
How does Auto Arima select the best parameters
上記のコードでは、我々は単に.fit() コマンドを使用して、p、q、d の組み合わせを選択することなく、モデルを適合させました。しかし、モデルはどのようにしてこれらのパラメーターの最適な組み合わせを見つけ出すのでしょうか。 Auto ARIMAでは、生成されたAIC値とBIC値を考慮して(コードにあるように)パラメータの最適な組み合わせを決定しています。 AIC (Akaike Information Criterion) と BIC (Bayesian Information Criterion) 値は、モデルを比較するための推定量です。 これらの値が低いほど、良いモデルです。
AIC および BIC の背後にある数学に興味がある場合は、以下のリンクをチェックしてください。 近道を知っていることは良いことですが、その背後にある数学に精通することも重要です。 この記事では、ARIMA がどのように機能するかの詳細についてざっと説明しましたが、記事内で提供されているリンクに必ず目を通しておいてください。
- A Comprehensive Guide to Time Series Forecast in Python
- Complete Tutorial to Time series in R
- 7 techniques for time series forecasting (with python codes)
練習問題でここで学習したことを練習してください: Time Series Practice Problem. また、同じ練習問題で作成したトレーニングコース「時系列予測」を受講することで、スタートダッシュができます
。