
Pythonでもっと学びたい方は、DataCampの無料コース「データサイエンスのためのPython入門」を受講ください。
皆さんはデータセットを見たことがあると思います。 小さい場合もありますが、時にはとてつもなく大きなサイズのものもよくあります。 少なくとも処理のボトルネックを引き起こすのに十分な大きさの、非常に大きなデータセットを処理するのは非常に困難になります。
では、これらのデータセットがこれほど大きくなる理由は何でしょうか。 それは、特徴量です。 特徴の数が多ければ多いほど、データセットは大きくなります。 しかし、必ずしもそうとは限りません。 特徴の数が非常に多くても、それほど多くのインスタンスを含んでいないデータセットもあります。 しかし、それはここでは重要ではありません。 高次元のデータセットには、まったく無関係な、重要でない、重要でない特徴が残っていることがよくあります。 これらのタイプの特徴の寄与は、重要な特徴と比較して、予測モデリングに対する貢献度が低い場合が多いことが分かっています。 また、寄与度がゼロである場合もある。
- これらの特徴に不必要なリソースを割り当てる。
- これらの特徴は、機械学習モデルがひどく悪いパフォーマンスをするノイズとして機能する。
特徴抽出とは、与えられたデータセットから最も重要な特徴を選択するプロセスである。 多くの場合、特徴量の選択は機械学習モデルのパフォーマンスを向上させます。
面白そうでしょう?
特徴量の選択とデータ サイエンスおよび機械学習の世界におけるその重要性について、非公式に紹介しました。 この投稿では、以下を取り上げます。
- 特徴選択への導入とその重要性の理解
- 特徴選択と次元削減の違い
- 特徴選択手法の異なるタイプ
- 異なる特徴選択手法の scikit-> による実装
- 特徴選択と次元削減の違い 特徴選択と次元削減の異なるタイプ
特徴選択入門
特徴選択は変数選択または属性選択としても知られています。
本質的には、最も重要な/関連性のあるものを選択するプロセスである。
特徴抽出の重要性を理解する
特徴抽出の重要性は、膨大な数の特徴を含むデータセットを扱うときに最もよく認識されるでしょう。 この種のデータセットは、しばしば高次元データセットと呼ばれる。 この高次元性により、機械学習モデルの学習時間が大幅に増加し、モデルが非常に複雑になり、その結果、過剰適合につながる可能性があります。 これらの冗長な特徴は、モデル学習にも効果的に寄与しない。 そのため、最も効果的な予測モデリング性能を得るために、データセットに対して最も重要で最も関連性の高い特徴を抽出する必要があることは明らかである。”
-変数選択と特徴選択の紹介
ここで、次元削減と特徴選択の違いを理解しましょう。
特徴選択は、次元削減と間違われることがあります。 しかし、これらは異なるものです。 特徴選択は、次元削減とは異なります。 どちらの方法もデータセットの属性の数を減らす傾向がありますが、次元削減の方法は属性の新しい組み合わせを作ることでそれを行う(特徴変換と呼ばれることもある)のに対し、特徴選択の方法はデータに存在する属性を変えずに含んだり除いたりしています。
次元削減法の例としては、主成分分析、特異値分解、線形判別分析などがあります。
ここで、特徴選択の重要性をまとめておきます。
- モデルの複雑さを軽減し、解釈を容易にする。
- 正しいサブセットを選択すれば、モデルの精度を向上させることができる。
次のセクションでは、一般的な特徴選択メソッドのさまざまな種類 – フィルター メソッド、ラッパー メソッド、および組み込みメソッド – について学習します。 Analytics Vidhya
フィルター法は、評価するデータの一般的な一意性に依存し、任意のマイニング アルゴリズムを含まず、特徴のサブセットを選択します。 フィルター法は、距離、情報、依存性、および一貫性を含む正確な評価基準を使用しています。 フィルター法は、ランキング手法の主要な基準を用い、変数の選択に順位付け法を用いる。 ランキング法を使用する理由は、シンプルで、優れた関連性のある特徴を生成することである。 ランキング法は、分類プロセスが始まる前に、無関係な特徴をフィルタリングする。
フィルター法は、一般にデータの前処理段階として使用される。 特徴の選択は、どの機械学習アルゴリズムにも依存しない。 特徴は統計的スコアに基づいてランク付けされ、結果変数と特徴の相関を決定する傾向がある。 相関は文脈に大きく依存する用語であり、作品によって異なる。 さまざまな種類のデータ (この場合は連続とカテゴリ) の相関係数を定義するために、次の表を参照できます。

画像ソース。 Analytics Vidhya
いくつかのフィルター手法の例としては、カイ二乗検定、情報利得、および相関係数スコアがあります。
次に、Wrapper メソッドについて説明します。
ラッパー メソッド
フィルター メソッドと同様に、ラッパー メソッドをより理解するために、同じ種類の情報グラフィックを提供しましょう:
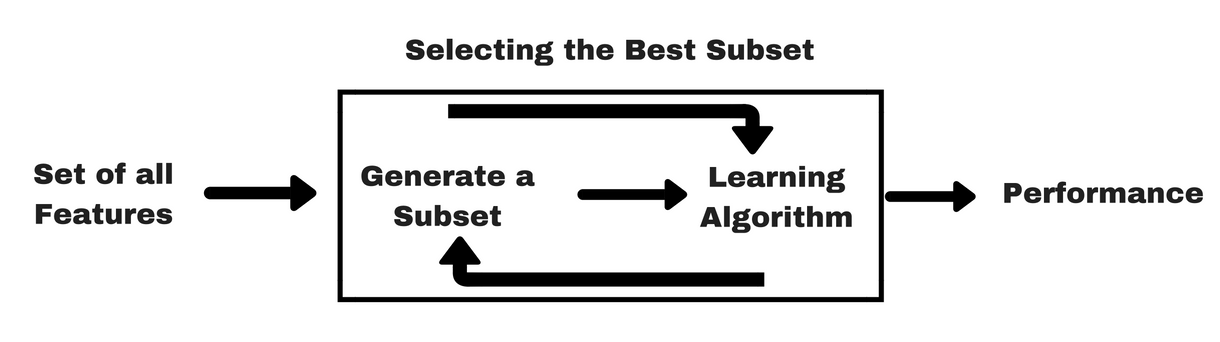
画像ソース。 Analytics Vidhya
上の画像でわかるように、ラッパー メソッドは 1 つの機械学習アルゴリズムを必要とし、そのパフォーマンスを評価基準として使用します。 この方法は、機械学習アルゴリズムに最適な特徴を探し出し、マイニング性能の向上を目指す。 特徴量の評価には、分類タスクに用いる予測精度や、クラスタリングを用いてクラスタの良さを評価する。
ラッパー法の代表例としては、前方特徴選択、後方特徴除去、再帰的特徴除去などがある
- 前方選択:前方選択とは、機械学習アルゴリズムに最適な特徴量を選択する方法である。 この手続きは、空の特徴量セットから始まる。 元の特徴の中から最適なものを決定し、縮小セットに追加する。 その後の各反復で、残りの元特徴のうち最良のものが集合に加えられる。
- Backward Elimination (後方削除)。 この手続きは、属性の完全なセットから始まる。 各ステップで、セット内に残っている最も悪い属性を削除する。
- 前方選択と後方排除の組合せ:前方選択と後方排除の組合せ。 段階的な前方選択と後方消去法は、各ステップで、手順が最良の属性を選択し、残りの属性の中から最悪のものを除去するように組み合わせることができる。
- Recursive Feature Elimination。 Recursive Feature Eliminationは、最も性能の良い特徴の部分集合を見つけるために貪欲な探索を行う。 繰り返しモデルを作成し、各反復で最も良いまたは最も悪い性能を持つ特徴を決定する。 すべての特徴が探索されるまで、左の特徴で後続のモデルを構築する。 そして、消去された特徴量の順番に順位をつける。
これで十分だ!
次に埋め込み手法を勉強しよう。
埋め込み手法
埋め込み手法は、モデル学習プロセスの各反復を引き受け、特定の反復のために学習に最も貢献する特徴を慎重に抽出する反復法である。 正則化手法は、係数のしきい値が与えられた特徴にペナルティを課す、最も一般的に使用される埋め込み手法です。
このため、正則化手法はペナルティ手法とも呼ばれ、予測アルゴリズム(回帰アルゴリズムなど)の最適化に追加の制約を導入して、モデルをより低い複雑性(より少ない係数)に偏らせるものです。
正則化アルゴリズムの例としては、LASSO、Elastic Net、Ridge Regression などがあります。
フィルター法とラッパー法の違い
さて、フィルター法とラッパー法の機能面での違いは、時に混乱することがあるかもしれません。
- フィルター法は、特徴の良し悪しを判断するために機械学習モデルを組み込んでいないのに対し、ラッパー法は機械学習モデルを使用して、それが不可欠かどうかを判断するために特徴を学習させます。 一方、ラッパー法は計算コストが高く、膨大なデータセットの場合、ラッパー法は考慮すべき最も効果的な特徴選択法ではない。
- フィルター法は、特徴の統計的相関をモデル化するためのデータが十分でない状況では、特徴の最適サブセットを見つけられないことがあるが、ラッパー法はその網羅性により常に特徴の最適サブセットを提供することが可能である。
- 最終的な機械学習モデルでラッパー メソッドからの特徴を使用すると、ラッパー メソッドがすでに特徴を使用して機械学習モデルを訓練しているため、オーバーフィットにつながり、学習の真の力に影響を与える可能性があります。 しかし、フィルターメソッドからの特徴は、ほとんどの場合オーバーフィッティングにつながりません。 また、さまざまな種類の特徴選択法も取り上げました。
重要な考慮事項
機械学習パイプラインにおける特徴選択の価値と、それが統合されるとどのようなサービスを提供するかをすでに理解されているかと思います。
簡単に言えば、特にクロスバリデーションなどの精度評価方法を使用している場合、学習用にデータをモデルに供給する前に特徴選択ステップを含める必要があります。 これにより、モデルが学習される直前に、データ フォルドに対して特徴選択が実行されるようになります。 しかし、最初に特徴選択を実行してデータを準備し、選択した特徴でモデル選択と学習を実行すると、それは失敗です。
すべてのデータで特徴選択を実行してからクロスバリデーションを行うと、クロスバリデーションの手順の各フォルダのテストデータも特徴の選択に使用されたことになり、機械学習モデルの性能に偏りが出る傾向があるのです。
Pythonでのケーススタディ
このケーススタディでは、Pima Indians Diabetesのデータセットを使用することになります。 データセットの説明はこちらにあります。
このデータセットは、8つの特徴に基づいて、人が糖尿病であるかどうかを予測する必要がある分類タスクに対応します。 最初のタスクは、データセットをロードして、処理を進めることです。 しかしその前に、必要な依存関係をインポートしましょう。
import pandas as pdimport numpy as np依存関係がインポートされたので、Pandasライブラリの助けを借りて、Pima IndiansデータセットをDataframeオブジェクトにロードしてみましょう。
data.head()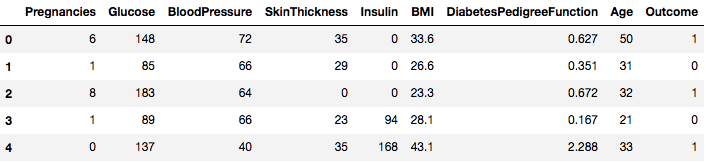
そこで、1 と 0 の結果にラベル付けされた 8 つの異なる特徴を見ることができ、1 は糖尿病を持つ観察を表し、0 は糖尿病を持っていないことを表します。 このデータセットには、欠損値があることが知られています。 具体的には、ゼロ値としてマークされたいくつかの列について、欠損オブザベーションがあります。 それらの列の定義によってこれを推測することができ、それらの測定値に対してゼロ値が無効であることは非現実的です、たとえば、以下のようになります。 body mass indexや血圧のゼロは無効です。
しかし、このチュートリアルでは、データセットの前処理されたバージョンを直接使用します。
# load dataurl = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"names = dataframe = pd.read_csv(url, names=names)あなたは今データフレームというDataFrameオブジェクトにデータをロードしました。
高速計算を行うためにDataFrameオブジェクトをNumPy配列に変換してみましょう。 また、データを別の変数に分離して、特徴とラベルが分離されるようにしましょう。
array = dataframe.valuesX = arrayY = arrayすばらしい!
まず、非負の特徴量に対するカイ二乗統計検定を実装して、データセットから最適な特徴量を4つ選択します。 カイ二乗検定はフィルタメソッドのクラスであることは既にご存知でしょう。
scikit-learn ライブラリは、特定の数の特徴量を選択するために、一連の異なる統計的検定で使用できる
SelectKBestクラスを提供しており、この場合、それはカイ二乗です。# Import the necessary libraries firstfrom sklearn.feature_selection import SelectKBestfrom sklearn.feature_selection import chi2実験を実行するために、ライブラリをインポートしました。 では、実際に見てみましょう。
# Feature extractiontest = SelectKBest(score_func=chi2, k=4)fit = test.fit(X, Y)# Summarize scoresnp.set_printoptions(precision=3)print(fit.scores_)features = fit.transform(X)# Summarize selected featuresprint(features)]解釈です。
各属性のスコアと、選ばれた4つの属性(スコアの高いもの):plas、test、mass、ageが表示されていますね。
追記:最初の行は特徴量の名前を示しています。
次に、ラッパー特徴選択法の一種であるRecursive Feature Elimination(RFE)を実装します。RFEは、再帰的に属性を削除し、残った属性でモデルを構築することで機能します。
モデルの精度を利用して、どの属性(および属性の組み合わせ)がターゲット属性の予測に最も貢献しているかを特定します。
RFEクラスについては、scikit-learnのドキュメントで詳しく説明しています。# Import your necessary dependenciesfrom sklearn.feature_selection import RFEfrom sklearn.linear_model import LogisticRegressionトップ3の特徴を選ぶために、
Logistic Regression分類器とRFEを使ってみましょう。# Feature extractionmodel = LogisticRegression()rfe = RFE(model, 3)fit = rfe.fit(X, Y)print("Num Features: %s" % (fit.n_features_))print("Selected Features: %s" % (fit.support_))print("Feature Ranking: %s" % (fit.ranking_))Num Features: 3Selected Features: Feature Ranking:RFEが上位3つの特徴を
preg,mass,pediと選んだことがわかります。これらはサポート配列でTrueと表示され、ランキング配列で選択肢「1」と表示されています。
次はリッジ回帰を使用します。これは基本的に正則化手法であり、同様に埋め込み特徴選択手法です。
この記事はリッジ回帰について優れた説明を提供します。
# First things firstfrom sklearn.linear_model import Ridge次に、リッジ回帰を使って係数R2を決定します。
また、scikit-learnのリッジ回帰に関する公式ドキュメントを確認します。
ridge = Ridge(alpha=1.0)ridge.fit(X,Y)Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None, normalize=False, random_state=None, solver='auto', tol=0.001)リッジ回帰の結果をより理解するため、小さなヘルパー関数を実装し、結果を解釈しやすいように出力するのを手伝います。
# A helper method for pretty-printing the coefficientsdef pretty_print_coefs(coefs, names = None, sort = False): if names == None: names = lst = zip(coefs, names) if sort: lst = sorted(lst, key = lambda x:-np.abs(x)) return " + ".join("%s * %s" % (round(coef, 3), name) for coef, name in lst)次に、リッジモデルの係数項をこの小さな関数に渡し、何が起こるかを見ます。
print ("Ridge model:", pretty_print_coefs(ridge.coef_))Ridge model: 0.021 * X0 + 0.006 * X1 + -0.002 * X2 + 0.0 * X3 + -0.0 * X4 + 0.013 * X5 + 0.145 * X6 + 0.003 * X7特徴変数が付加されたすべての係数項を見出すことができます。 これは、最も重要な特徴を選択するのに役立ちます。
- これは L2 正規化としても知られています。
- 相関のある特徴については、同様の係数を得る傾向があることを意味します。 しかし、多くの特徴を扱う複雑なシナリオでは、このスコアは最終的な特徴選択の意思決定プロセスで間違いなく役立ちます。 上記のセクションで実装した手法は、特定のデータセットの特徴を包括的に理解するのに役立つと思います。
- 特徴量の選択は、本質的に、あらゆる機械学習パイプラインで最も時間のかかる部分と考えられているデータ前処理の一部です。 より正確に特徴を解釈できるようになります。
まとめ!
この投稿では、最もよく研究され、よく調べられた統計トピックの1つ、つまり特徴選択を取り上げました。
このチュートリアルをさらに進めて、wrapper 法に相関尺度をマージして、それがどのように実行されるかを見ることができます。 その過程で、あなた自身の特徴選択メカニズムを作成することになるかもしれません。 そうやって、ちょっとした研究の基礎を確立していくのです。 また、研究者たちは、選択を行うために様々なソフトコンピューティングの原理を利用しています。 それ自体が一つの研究分野であり、研究対象です。
なぜこのような伝統的な特徴選択法が残っているのでしょうか?
そうですね、この疑問は当然です。 なぜなら、データから最も重要な特徴を抽出することが非常に可能なニューラル ネット アーキテクチャ (たとえば CNN) がありますが、これにも限界があるからです。 特定の特性(推移的特性、エッジ、位置的特性、輪郭など、典型的な画像が持つ特性)を持たない通常の表形式のデータセットにCNNを使うことは、最も賢明な判断とは言えません。 さらに、データやリソースが限られている場合、通常の表形式データセットでCNNを学習させることは、完全に無駄になってしまうかもしれません。
このトピックについてもっと掘り下げたい場合は、次のようなリソースがあります:
- Feature Selection for Knowledge Discovery and Data Mining
- Subspace, Latent Structure, and Feature Selection: 統計と最適化の視点ワークショップ
- Feature Selection: Problem statement and Uses
- Using genetic algorithms for feature selection in Data Analytics
以下は、このチュートリアルを書くために使用された参考文献です。 コンセプトとテクニック; Jiawei Han Micheline Kamber Jian Pei.
- 特徴選択入門
- 特徴選択に関するAnalytics Vidhyaの記事
- 階層モデルと混合モデル – DataCampコース
- 機械学習のための特徴選択 in Python
- 機械学習と特徴選択法によるストリームデータ中の外れ値検出
S. Visalakshi and V. Radha, “A literature review of feature selection techniques and applications”: Review of feature selection in data mining,” 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, 2014, pp.1-6.
.