細胞膜の透過性とは?
リーダーモード
すべての生物の特徴的な特徴の1つは、イオンと小分子の独特な混合物を含んでいるということです。 その組成は環境と異なるだけでなく、細胞内でも変化することがあります。 例えば、ある細胞区画の水素イオン濃度は他の区画の104倍にもなる(ミトコンドリアはpH8と高く、リソゾームはpH4と低い、BNID 107521, 106074)。 細胞外液と細胞内液のCa2+イオン濃度の比は、再び104倍となることがある(BNID 104083)。 この濃度差は非常に大きく、Ca2+イオンを膜を越えて細胞内区画から細胞外区画へ輸送するには、プロトン起電力勾配を下る1個以上のプロトンまたはナトリウムイオンのエネルギーが必要となるのです。 このことを理解するために、読者は、一桁の電位差を確立するためには6 kJ/mol (≈2 kBT) が必要であるという、「商売のコツ」のリストにある経験則を思い出す必要があります。 このエネルギーは、例えば60mVの電位差を1つの電荷が移動することで得られます。 4桁の濃度比を得るためには、約240mVの電子起電力(実際にはカルシウムイオンの二重電荷によりさらに大きい)を移動する電荷が必要である。 これは、「膜を隔てた電位差とは何か」のビネットで述べた膜の絶縁破壊電圧に非常に近い値である。 実際、Ca2+の高濃度比は通常、3つのナトリウムイオンの輸送またはATPの加水分解との結合によって達成され、膜に危険なエネルギーを与えずに必要な密度差を達成するのに役立つ。
熱力学の第二法則は、一般に、濃度勾配の存在は、システムを着実に平衡状態に導く物質輸送過程によって最終的に血流されると教えてくれている。 しかし、熱力学第二法則は、ある系の究極の状態(例えば、濃度が一様になること)の性質は教えてくれるが、その状態になるまでにどれくらいの時間がかかるかは教えてはくれない。 膜は、多くのイオン種や分子種の自発的な移動に対して非常に効果的な障壁を形成するように進化してきた。
平衡から少し離れた系の挙動を記述する「法則」の中で、大きな成功を収めたのが線形輸送法則である。 これらの法則は、ある量の輸送速度と関連する原動力の間に単純な線形関係を仮定している。 物質輸送の場合、フラックス(単位時間あたりに単位面積を横切る分子の数)と濃度差(関連する駆動力として機能する)の間に線形関係がある。 膜を介した輸送の場合、これらの考え方は(中性溶質の場合)j= – p-(cin-cout) という簡単な方程式に体系化されている。ここでjは細胞への純フラックス、cinとcoutは膜結合領域の内側と外側の濃度、pは透過性と呼ばれる物質パラメータである。 pの単位は、フラックスが数/(面積×時間)の単位を持ち、濃度が数/体積の単位を持つことに注目すれば、p自体の単位が長さ/時間であることが推論される。 多くの輸送量(例えば、30桁以上の大きさに渡る物質の電気伝導度)と同様に、透磁率は図1に示されるように非常に大きなダイナミックレンジを持っている。 図に見られるように、脂質二重層は1010倍近い範囲の透過性を持つ。
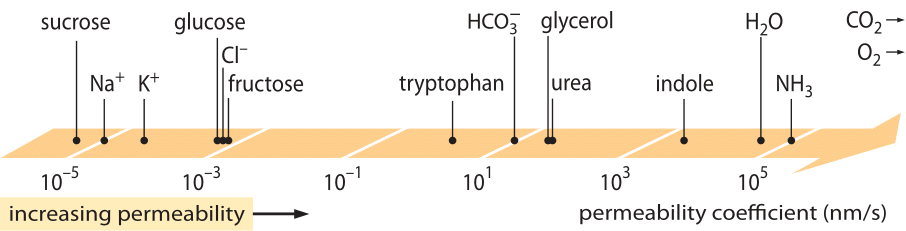
図1:細胞内のさまざまな化合物の膜透過性の広い範囲。 膜は電荷を持たない化合物に対してより透過性が高く、電荷を持つイオンに対しては最も透過性が低い。 イオンチャンネルが存在すると、それが開いているときの見かけの透過率が数桁高くなることに注意。 単位はnm/sとし、数nmを特徴的な膜幅とする。 図はR. N. Robertson, The Lively Membranes, Cambridge University Press, 1983から引用した。 グルコースの値は、BNID 110830, 110807 などのいくつかの資料から、Robertson の値より小さい。 その他のデータソース BNID 110729, 110731, 110816, 110824, 110806.
この透過性のスケールで化合物の位置を決めるにはどのような物理化学的パラメータがあるのだろうか。 一つの経験則は、小さな分子は大きな分子よりも透過性が高いということです。 もう一つの経験則は、中性化合物は同種の荷電化合物より何桁も速く膜を通過できることである。 帯電した化合物のうち、負(アニオン)の化合物は正(カチオン)の化合物よりはるかに高い透過性を持つ傾向がある。 疎水性とは、化合物が極性(水性)溶媒よりも非極性溶媒を好む傾向のことで、いわゆるオーバートン則と呼ばれるもので、膜の透過性は疎水性と共に増加する。 オーバートン則によると、イオンなどの荷電分子は膜を透過する際にエネルギー的なペナルティを受けるため透過性が低く、一方、酸素や二酸化炭素などの溶存ガスは荷電しておらず対称であるため疎水性が高く、透過性が高くなると予測されている。 実際、脂質二重膜のCO2に対する透過性は、0.01-1 cm/sという値を示し(そう、透過性の測定は研究室によって非常に大きな不確かさがある、BNID 110004, 110617, 102624)、図1に示した他のすべての値よりも高い値を示している。 この値は、細胞膜がつくるバリアが、細胞膜を外側から飲み込む撹拌されていない水の層がつくるバリアよりも、実際には障害になりにくいことを示している。 このような推論は、障害物の透過係数の式、p=K×D/l(lは幅、Dは拡散係数、Kは媒体と障害物の物質間の分配係数)で与えられることによって導き出すことができる。 これは、透水性の「溶解度-拡散」モデルとしても知られており、これらは透水性に影響を与える2つのステップであるKとDの効果を示している。 水の非撹拌層では媒体と非常に似ているためK=1だが、膜では最も疎水性の高い物質以外は通常1より数桁小さい値になる。このKへの依存性が、前述のオーバートンの法則の核心である。 また、CO2に対する高い透過性は、細胞内へのガス輸送に役立つとされていたアクアポリンのようなチャネルは、膜が十分な透過性を持っているため必要ないことも示唆している。 膜の特性が代謝物の化学組成にどのように影響するかを見るために、さまざまな化合物の漏出時間を計算してみました
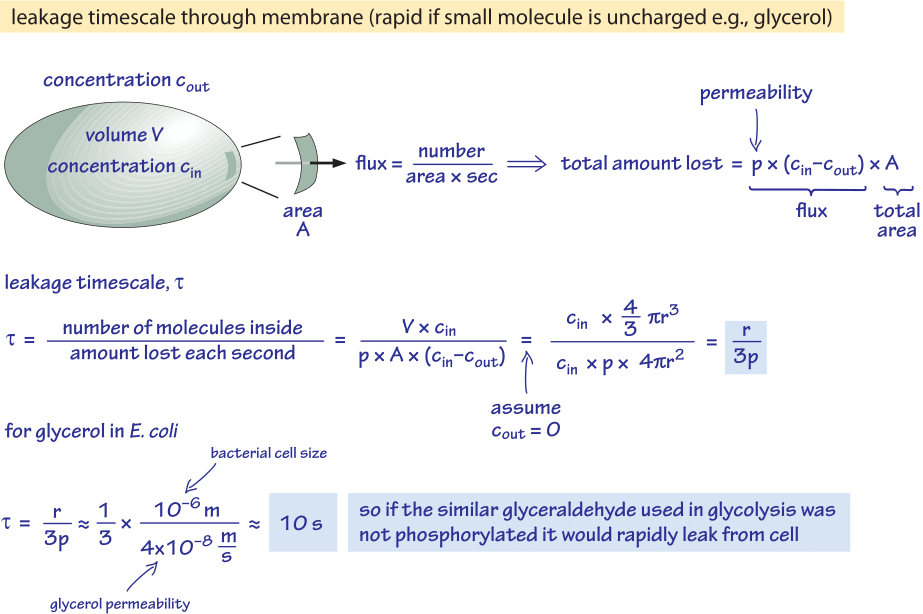
図2:リン酸化されていないグルコース分子が細菌細胞から受動的に拡散する時間尺度の包絡線計算結果。 次に、この効果が無視できる高速増殖細胞と、資源の著しい漏出を引き起こす可能性がある定常状態の細胞について、機能的な意味を検討する。
たとえば、グリセロールについて考えてみる。 図2に示す解析は、分子がリン酸化されたり、より親水性の高い形に変換されたりしない場合に、その分子が細胞外に漏れ出す時間を推定するものである。 図1から読み取れるように、グリセロールに対する細胞膜の透過性はp≈10-100 nm/s (BNID 110824)である。 細胞内への還流がない(cout=0)と仮定して、細胞内のグリセロール分子が周囲の培地に戻るまでの時間スケールは、細胞からの流出がp-A-cin(Aは細胞表面積)となることに注目すれば、大まかに見積もることが可能である。 時間スケールは、細胞内の総量V-cin(Vは細胞体積、より正確には細胞水体積)を取り、この流量を細菌細胞(r≈1μm)の時間スケールで割ることで求められる:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≒ 10 s.
これは、1/ln(2)の補正係数、すなわち2倍未満の増加を与える、時間とともに減少するcinの濃度を考慮していないため、粗い推定値である。 これらの推定から分かることは、グリセロールに非常によく似た解糖系中間体であるグリセルアルデヒドやジヒドロキシアセトンがリン酸化されず、電荷が付加された場合、細胞膜を通して拡散し、培地に失われてしまうということである。 炭素源が豊富に供給される実験用培地では、これは大きな問題ではない。しかし、細胞が定常期に栄養分の幸運なパルスを待つことが多い自然環境(E. 大腸菌は体外に排出された後、新しい宿主を見つけるまで何ヶ月も成長しないことがあると言われています)、細胞は代謝中間体が脂質二重層が示すバリアを再び通過しないような電荷を持つようにすることでその損失を抑えることができます。




