図形が1点を中心に描かれているとき、点対称が成り立つ。

この点を図形の中心または対称の中心と呼ぶ。 隣の図で、図上の点Xに対応して、中心の反対側にXに正対して図上にある点X’が存在することが分かる。
注意:
図形を180°回転して元の形に戻したとき、その図形には点対称性があると言う。
点対称性を示す図形の例。
●アルファベットのすべての文字。
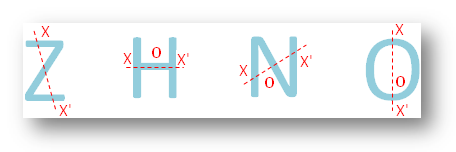
●幾何学図形の違い。
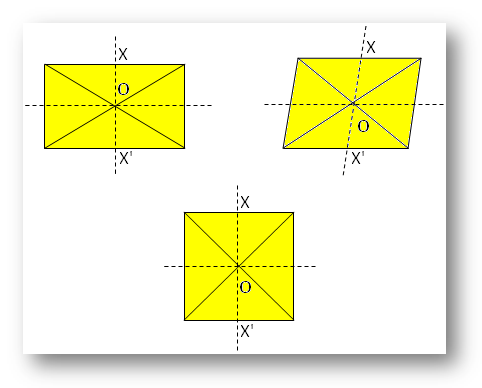
注:
ここで、O は対称の中心です。
Xに関して、X’ はOの反対側でXと正対するように存在します。
形状や図形が点対称性を満たす条件は何ですか?
すなわち、すべての部分が一致する部分
– 中心点からの距離が等しく
– しかし反対方向でなければならないこと。
●関連概念
●線対称
●回転対称
●回転対称の順序
●対称性の種類
●反射
●点のx-y方向の反射
●反射(reflective)軸
●Y- 軸の点の反射軸
●原点の反射
●回転
●90度時計回り回転
●90度反時計回り回転
●180度回転
7年生算数問題
8年生算数練習
点対称から HOME PAGE