ピアソンモード歪度

統計学定義 > ピアソンモード歪度

ピアソンの第一歪係数とも呼ばれ、分布の歪度を割り出す方法である。

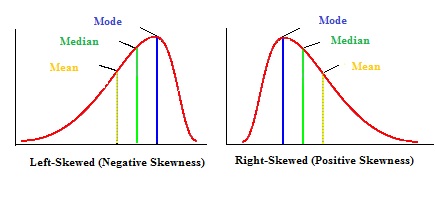
平均値、最頻値、中央値を使って、正または負の歪んだ分布かどうかを把握することができる。

• 平均が最頻値より大きい場合、その分布は正偏差である。
• 平均が最頻値より小さい場合、その分布は負偏差である。
• 平均が中央値より大きい場合、分布は正に歪んでいる。
• 平均が中央値より小さい場合、分布は負に歪んでいる。

Pearson Mode skewness

Pearson Mode skewnessは上記の事実を利用して、正の歪度か負の歪度かを調べるのに役立ちます。 分布があり、平均、最頻値、標準偏差(σ)がわかっている場合、ピアソンモード歪度の公式は次のようになります：

(mean-mode)/σ3909>

サンプル問題：平均19、最頻値20、標準偏差25のデータを持っているとします。 Pearson Mode Skewnessはこの分布について何を示していますか。
(mean-mode)/σ = (19-20)/25 = -0.04.
ごくわずかに負の歪度(-0.04)が存在することがわかります。 注：ほとんどの場合、歪度が非常に小さいので、これは対称分布とみなされます。

ピアソンモード歪度:

最頻値を知らなければ、Pearson mode skewnessは使えません。 しかし、歪度の方向は、平均値と中央値がどこにあるかを見つけることによっても把握することができます。 Business Statisticsによると、これは2番目の等価な式につながります：

3(Mean – Median) / σ

この式はPearsonの第2歪度係数とも呼ばれます。

Pearsonのモード歪度。 結果が意味するもの

平均値と最頻値、または平均値と中央値の差は、分布がどの程度対称性から外れているかを教えてくれます。 対称な分布（例えば、正規分布）は、歪度が0です。
両方の式は、平均からの測定の無次元単位である標準偏差で結果を与えます。

Dodge, Y. (2008). コンサイス・エンサイクロペディア・オブ・スタティスティックス(The Concise Encyclopedia of Statistics). Springer.
Gonick, L. (1993)。 統計学への漫画のガイド. HarperPerennial.
Klein, G. (2013). 漫画でわかる統計学入門. ヒル & ワムグ.
ヴォーグ, W.P. (2005). 統計学辞典 & Methodology: 社会科学のためのノンテクニカルガイド. SAGE.

———————————————————-

Need help with a homework or test question? Chegg Studyでは、その分野の専門家からステップバイステップの解決策を得ることができます。 Cheggのチューターとの最初の30分間は無料です!