始める前に、いくつかの仮定をしなければなりません。
まず、私たちはニュートン流体で作業しています。 これは流体の粘性を説明する最も簡単な数学的方法である。 完全にこの範疇に入る現実の流体はありませんが、ほとんどの場合、空気と水はニュートン流体として扱うことができます。 もう一つ非常に重要な仮説は、流体は非圧縮性であるということです。 これは、その密度 rho が一定であることを意味します。
Conservation of mass

最初の方程式は、扱っている流体の質量は保存されていると教えてくれています。 流体はその形を変えることができますが、この方程式は質量が最初から最後まで同じ形であることを教えてくれます。
さて、数学の話をしましょう。 uという文字は流体の速度を表し、それはベクトルである。 u、v、wと呼ぶことができ、これらはx、y、z方向への流体の速度を表します。 ギリシャ文字の nabla ∇ の後にドットをつけたものが発散演算子です。 これは、その成分をすべての方向(この場合は x、y、z)で微分することを意味します。

1次微分は速度のx成分がx方向の移動に伴ってどう変わるかを教えてくれています。 他の2つの微分も同様です。 この式は0に等しいので、質量が保存されていることを示しています。
運動量の保存

2番目の方程式は実際には3つの微分方程式がセットになっているのですが、この方程式は、運動量の保存の方程式として知られているのです。 これは流体に対するニュートンの第二法則と言えるものである。 式を展開すると複雑な系になります。
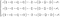
もっと簡単なので、展開しない運動量の保存に集中することにします。
流体を扱う場合、質量と密度は(体積が同じであれば)同じものであると言えます。 2つの流体を考える場合、密度の高い方が「重い」と言えます(例えば、水銀と水など)。 この場合、ギリシャ文字のρ(ロー)は流体の密度を表します。
質量がわかったところで、ニュートンの第二法則に戻ると、加速度が必要です。 それはまさに速度ベクトルの時間微分の結果です。

さて、残るは等号の右側の項で、これは流体にかかるすべての力を表しています。
第1項∇pは圧力の勾配である。 これは、流体が含まれる空間の圧力の差を表します。 例えば、圧力の低い部分と高い部分があれば、流体は圧力の高い部分から低い部分に移動します。 pの勾配はそのすべてを言っているのです。
第2項は流体の粘性を表しています。 水と蜂蜜のような2つの異なる液体について考えてみましょう。 コップに水を注ぐと、それはすばやく簡単に落ちます。 あなたが蜂蜜で同じことをするとき、それは粘着性があり、それは非常にゆっくりと注ぎます。 これはこの式が言っていることです。
最後の項、Fは、その流体に加えられる可能性のあるすべての外力を表すので、最も簡単なものです。 通常、ここで考える力は重力です。
これです。これらの派手な記号や文字の意味は、力=質量×加速度だけです。
ナビエ・ストークス方程式の使用
これらの方程式を解くことは非常に複雑なので、使用するには多くの近似を行う必要があります。 たとえば、ポアズイユ流とクーエット流があります。 この2人の科学者は、多くの仮定を用いて、非常に特殊なアプリケーションのためのナヴィエ・ストークス方程式の解を見つけることができました。 しかし、天気予報のようなもっと複雑な仕事に使いたい場合は、別の方法をとる必要があります。
これらの方程式を使う最も一般的な方法は、レイノルズ平均を使って、方程式を変形することです。 これは高度な数学的処理で、その結果がレイノルズ方程式となります。 これらは通常RANS(レイノルズ平均ナビエ・ストークス方程式という意味)方程式と呼ばれます。
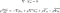
これらの式は流体が乱流であるとき使用されるものです。 最後の項を除けば、ナビエ・ストークス方程式とほとんど同じです。 これはレイノルズ応力テンソルと呼ばれるものである。 これは、流体の乱れを考慮するための量である。
RANS方程式では、使用する量は時間間隔で平均化される。 この間隔は、研究している現象の観測を可能にするのに十分小さくなければならない。 同時に、乱流効果の重要性を失わせるほど大きくなければならない。
正しい仮定があれば、これらの方程式は機能する。 私たちは、F1 カーを速くするため、宇宙船を ISS に行かせるため、そして天気予報を作るために、これらの方程式をどのように使うかを知っています。
100万ドルの賞金
物理学の観点からは、これらの方程式は、流体で機能するニュートンの第二法則にすぎません。 いくつかの仮定といくつかの簡略化をすると、それらを使って驚くべきことができるのです。
本当の問題は、これです。 近似なしにこれらの方程式を解くのは、とにかくひどく複雑です。 あまりに難しいので、解が実際に存在することが証明されていないのです。
問題の公式声明(こちらを参照)は次のとおりです:
空間と時間の3次元において、初期速度場を与えると、ナビエ・ストークス方程式を解く、滑らかでグローバルに定義されたベクトル速度とスカラー圧力場が存在することを証明または反例を与えてください。
これが意味するところは、賞を獲得するためには次の3つのことをしなければならないということです:
- 解が存在することを証明する
- 空間のすべての点に解が存在しなければならない
- 解が滑らかでなければならない。 つまり、初期条件を少し変えただけで、結果が少し変わるだけである。
技術者は通常、これらの方程式が、たとえある程度の近似値であっても、機能すると知っていれば十分である。 しかし、数学者にとっては、解が存在するかどうか、そして解がどのように振る舞うかを知ることが非常に重要です。
あなたは今、このまま動くなら、証明を探すのに時間とエネルギーを使うのはまったく無駄なことだと考えているかもしれません。 まあ、人類の歴史における多くの技術的進歩のように、結果はあまり重要でないように思えるかもしれません。 重要なのは、そこに至る道筋であり、それによって私たちの生活に新しい知識と改善をもたらすことができるのです。
宇宙ミッションについて考えてみましょう。 もし人類が月に行って歩くと決めなければ、私たちの生活を向上させるために使われる多くの物体を手に入れることはできなかったでしょう。 MRI装置やペースメーカーは、宇宙探査のために開発された技術から生まれたものです。 現在、世界中の医師が、命を救うために毎日使っています。 これと同じことが言えます。 ナビエ・ストークス方程式の解を発見するまでの道のりは、流体に対する理解を深めることにつながるでしょう。 新しい発見につながることもあり、おそらく新しい数学の発明が必要になるでしょう。 そして、このことは、他の多くの問題に答えるために、また、私たちの生活を改善し、私たちをより良くするための新しい技術を発明するために利用することができるのです
。