もしあなたが飲み物が好きなら、クラインの瓶はお勧めできない入れ物です。 見た目は何となく瓶のようですが、容積を囲んでいないので、実際には液体を入れることができないのです。
このような奇妙なものをどのように作り、なぜ作ろうと思ったのでしょうか。 1882年にボトルを発見した数学者のフェリックス・クラインは、「ゴム管の一部を反転させ、外側と内側が出会うように自分自身を通過させることによって視覚化できる」表面と表現しています。
Your browser does not support the video tag.Direct link
クラインの瓶が、より馴染みのある球と同様に閉曲面であることは明らかです。空間の有限な領域に収めることができるという意味で有限ですが、アリはその上を永遠に歩き回ることができ、境界線に遭遇したり縁から落ちたりすることはありません。 内と外がある球面とは異なり、クラインの瓶は一面的であり、アリは歩いて表面の各点の両側に到達することができる。 このように、クラインボトルは体積を持たない。また、「なぜ」という問いにも答えている。 (クラインの瓶のとてもきれいな絵はこちら)

メビウスの輪は一面です – アニメーション版をご覧ください。 (画像とアニメーションは Konrad Polthier 氏によるものです。)
これが少しわかりにくいようでしたら、もっと簡単な片面曲面の例、有名なメビウスの帯を思い浮かべてみてください。 短冊の両端を取り、ひねって、接着剤で貼り合わせれば作れます。 緑とオレンジのように色が違う紙を使えば、メビウスの帯が片面であることを簡単に納得させることができます。 一度ねじって接着すれば、紙を突き破ったり、紙の端を乗り越えたりしなくても、すべての緑の点からすべてのオレンジの点に到達できることがわかる。
クラインの瓶とは異なり、メビウスの帯には境界がある–それは元の帯の接着していない二つの端で構成されている。 しかし、この2つの間にはつながりがあります。
Your browser does not support the video tag.Direct link
帯で結ばれています。
この事実から、数学者のレオ・モーザーは次のような詩を詠んだ:
A mathematics named KleinThought the Möbius band is divine.Said he.This is a limerick: “If you glue The edges of two, You’ll get a weird bottle like mine.”
数学者の中には本当に多才な人がいる!
クラインの瓶のもう一つの不思議な特徴は、それ自身が交差しているということで、クラインの提案したように一本のゴムチューブから作るのは難しいということである。 厳密に言えば、上に描かれた自己交差する物体はクライン瓶ではなく、(クラインが示したように)クライン瓶を視覚化したものに過ぎないのです。 その理由を知るには、まず、より身近なドーナツ(数学的にはトーラスとして知られている)を思い浮かべてみてほしい。 正方形のゴムシートからトーラスを作るには、まず2つの対向する側面を接着して円柱を作り、その円柱の2つの境界成分を接着してトーラスを得ます。

トーラスを作る。
接着を面倒くさがるなら、トーラスを単に正方形と考え、反対側の辺の反対点は同じと考えることに留意すればよい。 つまり、「正方形」の上に描いた図形を上辺にスライドさせると下辺に再び現れ、右辺にスライドさせると左辺に再び現れます(逆も然り)。
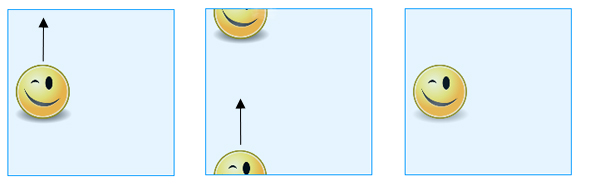
「正方形」に描いた図形を上辺にスライドさせると、下辺に再び現れる。
真のクライン瓶を得るには、同じ方法で、正方形の対向する辺上の対極点を確認することから始める。 ただし、もう一組の辺については、図のように正対する点ではなく、斜めに対向する点を特定する。
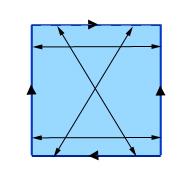
クラインボトルの作り方:対向する2辺(この絵では縦の辺)の対極点を特定し、残りの2辺の対角線上の対極点を特定します。 (上下の辺の点に左から0~1の数字でラベルをつけると、上の辺のラベルxの点は下の辺のラベル1-xの点と一致します。)
こうしてできたものがクラインびんです。 ここでも、どの境界点を同一視するかに留意して、正方形として考えることができる。 反対側の点が特定された辺(この図では縦)の上に図形を滑らせると、先ほどと同じように反対側に再び現れる。 しかし、点が斜めに特定された辺(図では水平)の上に図形を滑らせると、反対側に現れますが、元の自分の鏡像のようにずれて見えます。
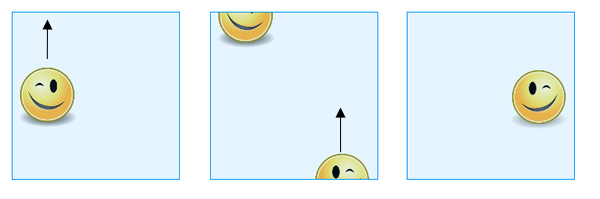
上の辺の上に図形をスライドさせると、下の辺を横切って現れますが、反対側にずれて元の自分の鏡像として現れます。
実際に点を接着して三次元空間にこの図形を構築するには、自分自身を交差させるようにするしかありません。 これは元の正方形の内部にある点の組を特定することに等しいので、厳密に言えば、出来上がった形状は境界点しか特定されていないクラインの瓶と全く同じではありません。 あくまで3次元空間におけるボトルの表現方法の1つに過ぎないのです(他にもあります)。
Your browser does not support the video tag.Direct link
Mirror image and orientability(鏡像と配向性)。 Konrad Polthierによるアニメーション。
不思議なことに、「内側」「外側」「片側」という概念は、オブジェクトが置かれている周囲の空間によって異なります。 たとえば、(2 次元空間の)紙の上に描かれたループは内側と外側がきちんと定義されていますが、3 次元空間に描かれたループはそうではありません。 だから、3次元空間にどのように面を埋め込むかを決めないと、片面性というのは語れないのである。 しかし、これと密接に関連する性質として、周囲の空間に依存しない、形状に固有な性質がある。 表面上に描かれた図形を、その鏡像のように見えるように滑らせて元の位置に戻すことができない場合、その表面は「方向づけ可能」と呼ばれます。 右の画像に付随するアニメーションでわかるように、メビウスの帯は配向可能ではありません。 そして、上のスマイリーフェイスの画像からわかるように、クラインの瓶もそうではありません。数学的に完全に説明すると、クラインの瓶は閉じた、向きの定まらない表面です。 クライン瓶についてもっと知りたい方は、Inside the Klein bottleの記事を参照してください。
著者について
Marianne FreibergerはPlus.の編集者です
。