La simmetria del punto esiste quando la figura è disegnata intorno a un solo punto.

Questo punto è chiamato il centro della figura o il centro della simmetria. Nella figura adiacente, osserviamo che in corrispondenza del punto X sulla figura, esiste un punto X’ dall’altra parte del centro che è direttamente opposto a X e giace sulla figura. Diciamo che la figura è simmetrica rispetto al centro.
Nota:
Quando ruotiamo una figura di circa 180° ed essa riacquista la sua forma originale, allora diciamo che esiste una simmetria puntiforme nella figura.
Esempi di figure che mostrano la simmetria puntiforme:
● Tutte le lettere dell’alfabeto inglese.
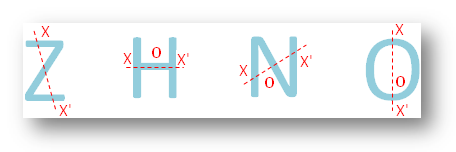
● Figure geometriche diverse.
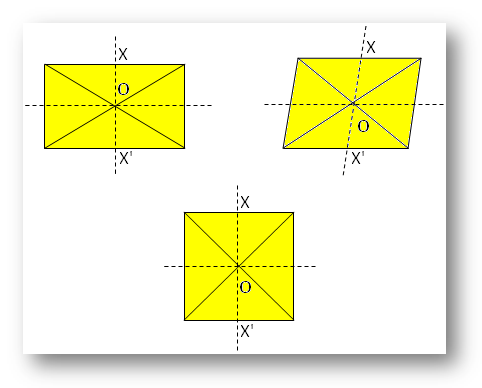
Nota:
Qui O è il centro di simmetria.
Per quanto riguarda X esiste X’, tale che X’ è direttamente opposto a X sull’altro lato di O.
Quali sono le condizioni che una forma o una figura soddisfa per la simmetria puntiforme?
Le condizioni che una forma o una figura soddisfa per la simmetria puntiforme sono: ogni parte deve avere una parte corrispondente
– la distanza deve essere uguale dal punto centrale
– ma deve essere in senso contrario.
● Concetti correlati
● Simmetria lineare
● Linee di simmetria
● Simmetria rotazionale
● Ordine di simmetria rotazionale
● Tipi di simmetria
● Riflessione
● Riflessione di un punto sull’asse x-
● Riflessione di un punto sull’asse y
● Riflessione di un punto nell’origine
● Rotazione
● Rotazione di 90 gradi in senso orario
● Rotazione di 90 gradi in senso antiorario
● Rotazione di 180 gradi
Problemi di matematica di quinta elementare
Pratica di matematica di terza media
Dalla simmetria del punto alla HOME PAGE